Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Сфера и шар Лауреат

Содержание

Цель урока 1)Вывести понятие сферы, шара, и их элементов. 2)Вывести уравнение сферы в заданной прямоугольной системе координат 3)Формировать навык решения задач по данной теме.
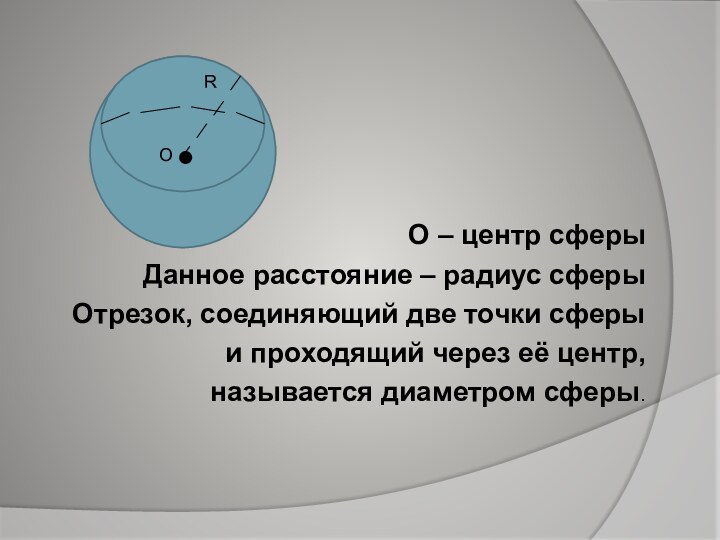
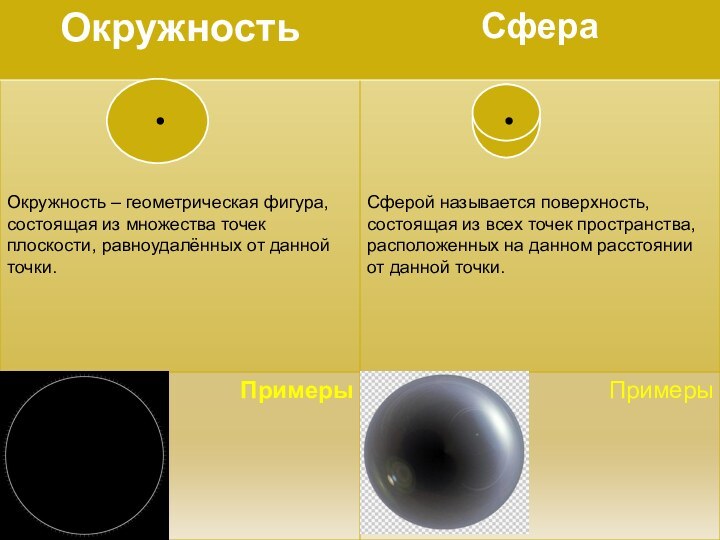
Сфера и шар Цель урока 1)Вывести понятие сферы, шара, и их элементов. 2)Вывести уравнение сферы в заданной О – центр сферыДанное расстояние – радиус сферыОтрезок, соединяющий две точки сферы Предметы окружающей обстановки, дающие представление о сфере Предметы окружающей обстановки, дающие представление о шаре Сфера, как тело вращения Вывод: Сфера может быть получена вращением полуокружности вокруг её диаметра.АСВ Сфера может быть получена вращением полуокружности вокруг её диаметра, а шар – №573 Уравнение сферы Вывести уравнение сферы с центром в начале координатx²+y²+z²=R² Назовите координаты центра и радиус сферы, заданной уравнением.1)x²+y²+z²=492)(х-3)²+(у+1)²+(z+3)²=13)X²+(y-4)²+z²=34)(x-1)²+y²+(z+2)²=25 Напишите уравнение сферы радиуса R с центром А, если 1)А(1;0;-2),R=22)A(-1;-1;-1), R=3)A(0;0;0), R=14)A(5;0;0), R=6 №579(а , г) Итог урока1)Дайте определение сферы2)Дайте определение шара3)Как может быть получена сфера, шар?4)Какой вид имеет уравнение сферы? Домашнее задание:п.58,п.591 уровень
Слайды презентации

Слайд 2 Цель урока
1)Вывести понятие сферы, шара, и их элементов.
2)Вывести

Цель урока 1)Вывести понятие сферы, шара, и их элементов. 2)Вывести уравнение сферы в

уравнение сферы в заданной прямоугольной системе координат
3)Формировать навык решения

задач по данной теме.

Слайд 3

Слайд 4





О – центр сферы
Данное расстояние – радиус сферы
Отрезок,

О – центр сферыДанное расстояние – радиус сферыОтрезок, соединяющий две точки

соединяющий две точки сферы
и проходящий через её центр,

называется диаметром сферы.

R

О

Слайд 5 Предметы окружающей обстановки, дающие представление о сфере

Предметы окружающей обстановки, дающие представление о сфере

Слайд 6

Слайд 7 Предметы окружающей обстановки, дающие представление о шаре

Предметы окружающей обстановки, дающие представление о шаре

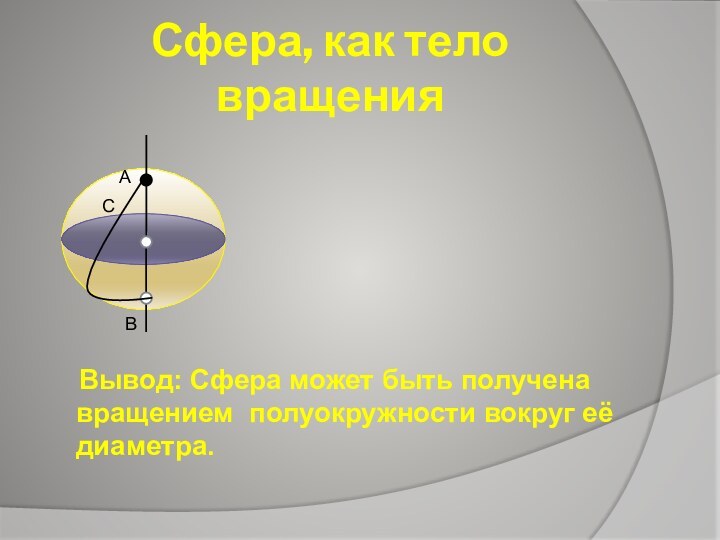
Слайд 8 Сфера, как тело вращения






Вывод: Сфера может быть получена

Сфера, как тело вращения Вывод: Сфера может быть получена вращением полуокружности вокруг её диаметра.АСВ

вращением полуокружности вокруг её диаметра.
А
С
В

Слайд 9 Сфера может быть получена вращением полуокружности вокруг её

Сфера может быть получена вращением полуокружности вокруг её диаметра, а шар

диаметра, а шар – вращением полукруга вокруг его диаметра.

Слайд 10 №573

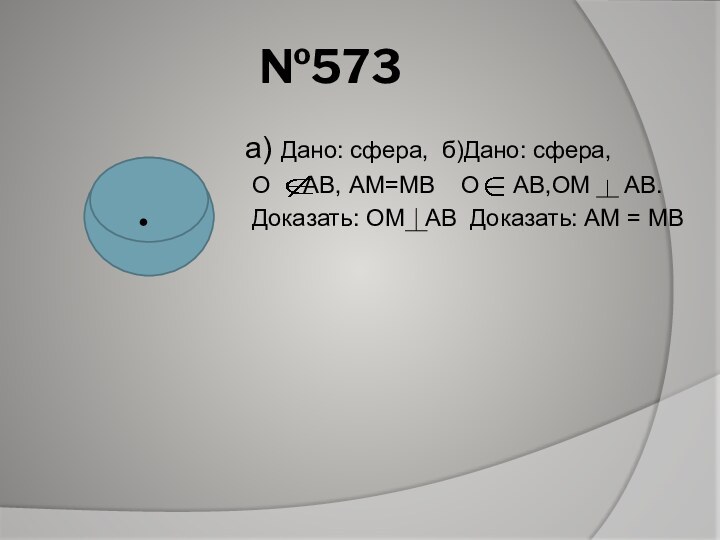
№573 а) Дано: сфера, б)Дано: сфера,

а) Дано: сфера, б)Дано: сфера,

О АВ, АМ=МВ О АВ,ОМ АВ.
Доказать: ОМ АВ Доказать: АМ = МВ

Слайд 11 Уравнение сферы

Уравнение сферы

Дано : сфера, R, С ,
М (x; y; z)
Доказать:



Доказательство:
1)Найти расстояние от точки до


2) MC=R

3)


z

x

y

M (x; y; z)

Слайд 12 Вывести уравнение сферы с центром в начале координат

x²+y²+z²=R²

Вывести уравнение сферы с центром в начале координатx²+y²+z²=R²

Слайд 13 Назовите координаты центра и радиус сферы, заданной уравнением.

1)x²+y²+z²=49
2)(х-3)²+(у+1)²+(z+3)²=1
3)X²+(y-4)²+z²=3
4)(x-1)²+y²+(z+2)²=25

Назовите координаты центра и радиус сферы, заданной уравнением.1)x²+y²+z²=492)(х-3)²+(у+1)²+(z+3)²=13)X²+(y-4)²+z²=34)(x-1)²+y²+(z+2)²=25

Слайд 14 Напишите уравнение сферы радиуса R с центром А,

Напишите уравнение сферы радиуса R с центром А, если 1)А(1;0;-2),R=22)A(-1;-1;-1), R=3)A(0;0;0), R=14)A(5;0;0), R=6

если
1)А(1;0;-2),R=2
2)A(-1;-1;-1), R=
3)A(0;0;0), R=1
4)A(5;0;0), R=6

Слайд 15
№579(а , г)

№579(а , г)

Слайд 16 Итог урока
1)Дайте определение сферы
2)Дайте определение шара
3)Как может быть

Итог урока1)Дайте определение сферы2)Дайте определение шара3)Как может быть получена сфера, шар?4)Какой вид имеет уравнение сферы?

получена сфера, шар?
4)Какой вид имеет уравнение сферы?

  • Имя файла: sfera-i-shar-laureat.pptx
  • Количество просмотров: 149
  • Количество скачиваний: 0
- Предыдущая Альберт Эйнштейн
Следующая - Компоненты ландшафта

Похожие презентации

Презентация по геометрии на тему Площади (8 класс) Презентация по геометрии на тему Площади (8 класс) 144
Симметрия в нашей жизни Симметрия в нашей жизни 257
Понятие движения Понятие движения 155
Числовая окружность Числовая окружность 154
Наглядная геометрия Наглядная геометрия 163
Смежные и вертикальные углы-презентация Смежные и вертикальные углы-презентация 132
Геометрия. Треугольник и его элементы Геометрия. Треугольник и его элементы 174
Геометрические преобразования в пространстве Геометрические преобразования в пространстве 156
Презентация по математике на тему Площадь треугольника 8 -9 классы Презентация по математике на тему Площадь треугольника 8 -9 классы 152
История развития геометрии История развития геометрии 153
Геометрия в живописи. Геометрические мотивы в работах Кандинского В.В. и Анри Руссоу Геометрия в живописи. Геометрические мотивы в работах Кандинского В.В. и Анри Руссоу 80
Презентация по геометрии на тему Треугольники Презентация по геометрии на тему Треугольники 181
Актуальность изучения предмета: черчение Актуальность изучения предмета: черчение 159
Введение в геометрию Введение в геометрию 157
Квадрат Пирсона Квадрат Пирсона 147
Перпендикулярность прямой и плоскости Перпендикулярность прямой и плоскости 163
Презентация к уроку Компланарные векторы Презентация к уроку Компланарные векторы 151
Проекции прямой Проекции прямой 173
Презентация по геометрии в 11 классе на тему:Конус. Решение задач Презентация по геометрии в 11 классе на тему:Конус. Решение задач 186
Применение подобия треугольников при решении задач. Применение подобия треугольников при решении задач. 281
Презентация к уроку геометрия в 8 классе Теорема Пифагора Презентация к уроку геометрия в 8 классе Теорема Пифагора 153
Презентация к уроку геометрии 11 класса Площадь поверхности конуса. Решение задач. Презентация к уроку геометрии 11 класса Площадь поверхности конуса. Решение задач. 173
Фигуры вращения Фигуры вращения 192
Презентация по геометрии на тему Геометрические фигуры в нашей жизни ученицы 9 класса Презентация по геометрии на тему Геометрические фигуры в нашей жизни ученицы 9 класса 209
Построение сечений многогранников Построение сечений многогранников 139
Замечательные кривые Замечательные кривые 171
Нахождение площадей многоугольников Нахождение площадей многоугольников 147
Подобные треугольники Подобные треугольники 172
Август Фердинанд Мёбиус Август Фердинанд Мёбиус 151
От сферы к плоскости От сферы к плоскости 148