Слайд 2
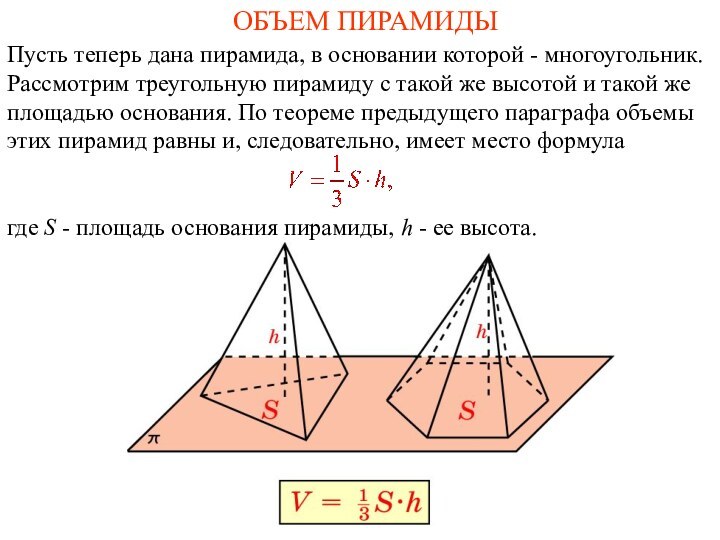
ОБЪЕМ ПИРАМИДЫ
Пусть теперь дана пирамида, в основании которой
- многоугольник. Рассмотрим треугольную пирамиду с такой же высотой
и такой же площадью основания. По теореме предыдущего параграфа объемы этих пирамид равны и, следовательно, имеет место формула
где S - площадь основания пирамиды, h - ее высота.
Слайд 3
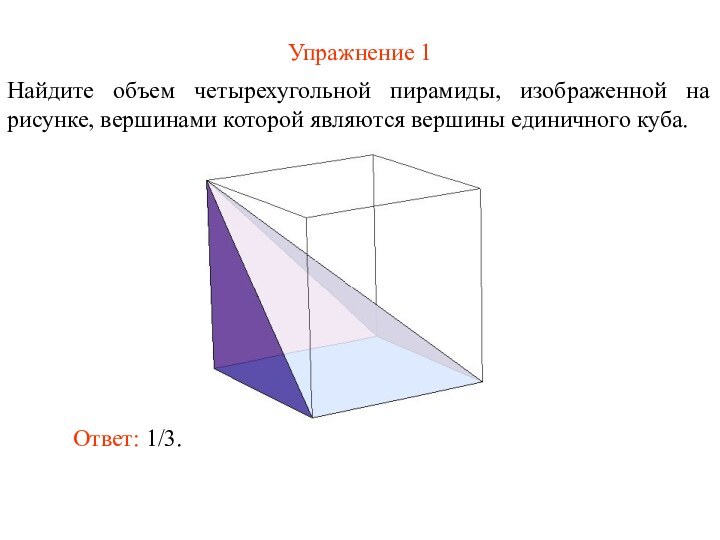
Упражнение 1
Найдите объем четырехугольной пирамиды, изображенной на рисунке,
вершинами которой являются вершины единичного куба.
Ответ: 1/3.
Слайд 4
Упражнение 2
Найдите объем треугольной пирамиды, изображенной на рисунке,
вершинами которой являются вершины единичного куба.
Ответ: 1/6.
Слайд 5
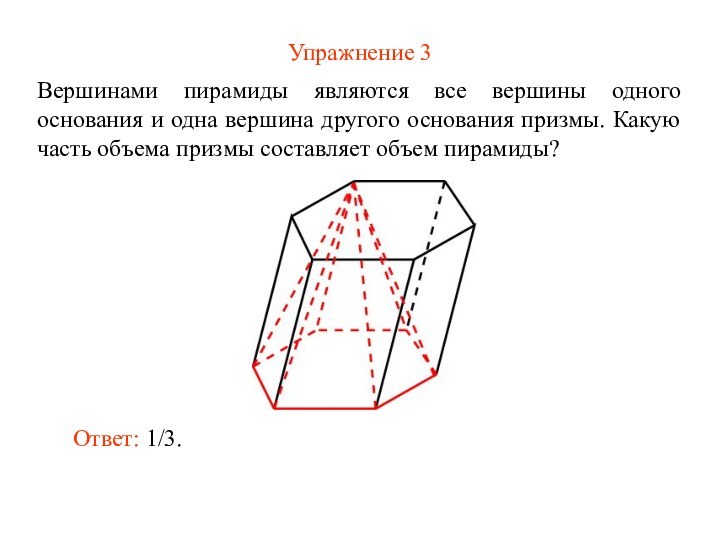
Упражнение 3
Вершинами пирамиды являются все вершины одного основания
и одна вершина другого основания призмы. Какую часть объема
призмы составляет объем пирамиды?
Ответ: 1/3.
Слайд 6
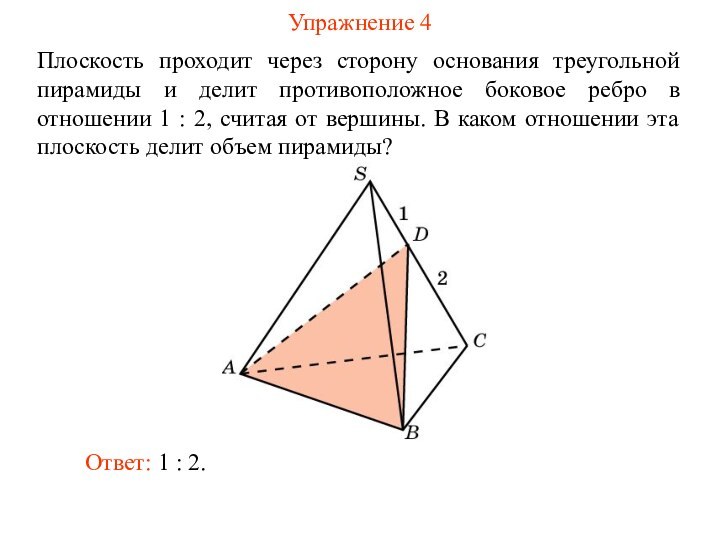
Упражнение 4
Плоскость проходит через сторону основания треугольной пирамиды
и делит противоположное боковое ребро в отношении 1 :
2, считая от вершины. В каком отношении эта плоскость делит объем пирамиды?
Ответ: 1 : 2.
Слайд 7
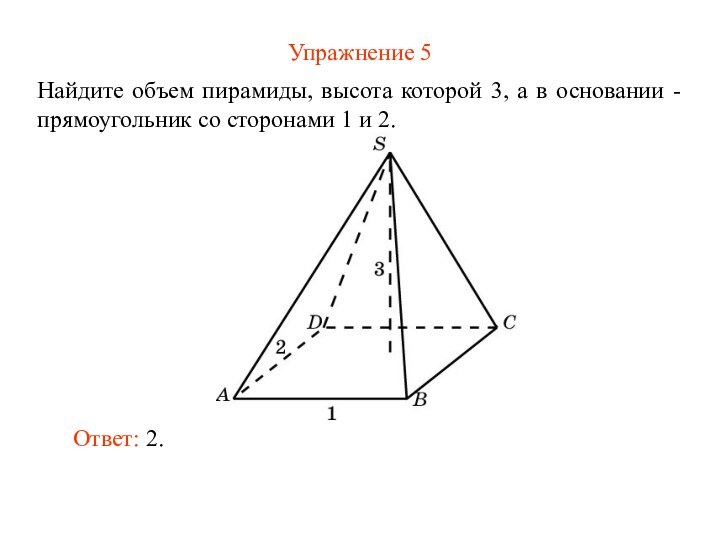
Упражнение 5
Найдите объем пирамиды, высота которой 3, а
в основании - прямоугольник со сторонами 1 и 2.
Ответ:
2.
Слайд 8
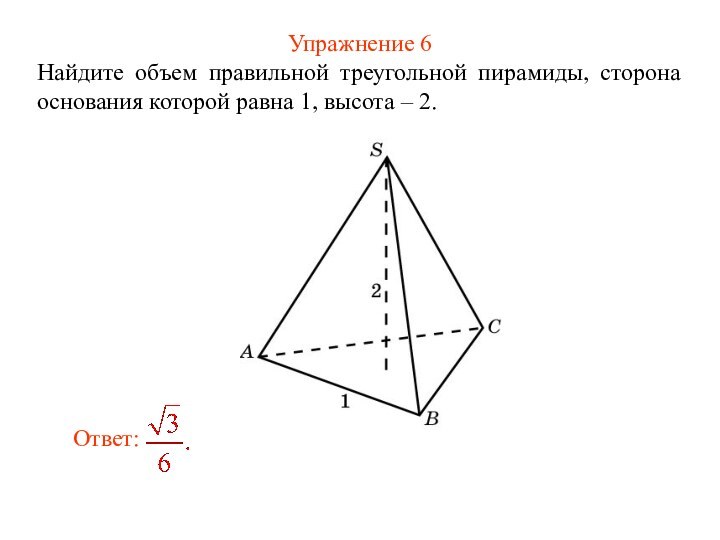
Упражнение 6
Найдите объем правильной треугольной пирамиды, сторона основания
которой равна 1, высота – 2.
Слайд 9
Упражнение 7
В правильной четырехугольной пирамиде высота 3 м,
боковое ребро 5 м. Найдите ее объем.
Ответ: 32 м3.
Слайд 10
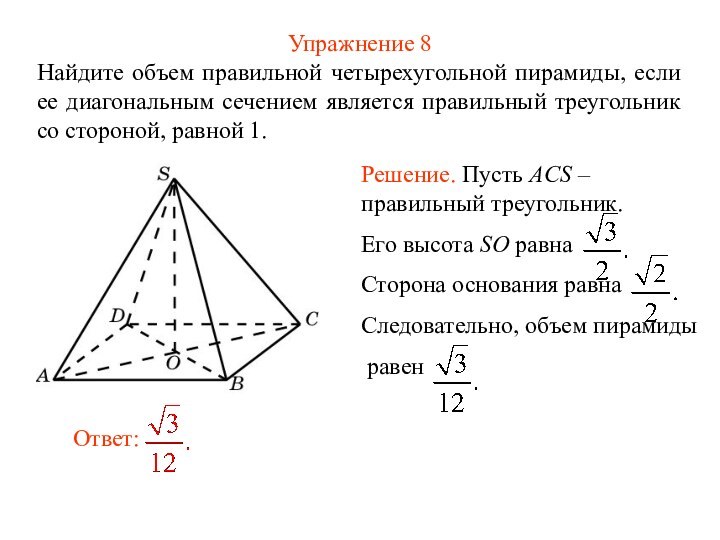
Упражнение 8
Найдите объем правильной четырехугольной пирамиды, если ее
диагональным сечением является правильный треугольник со стороной, равной 1.
Слайд 11
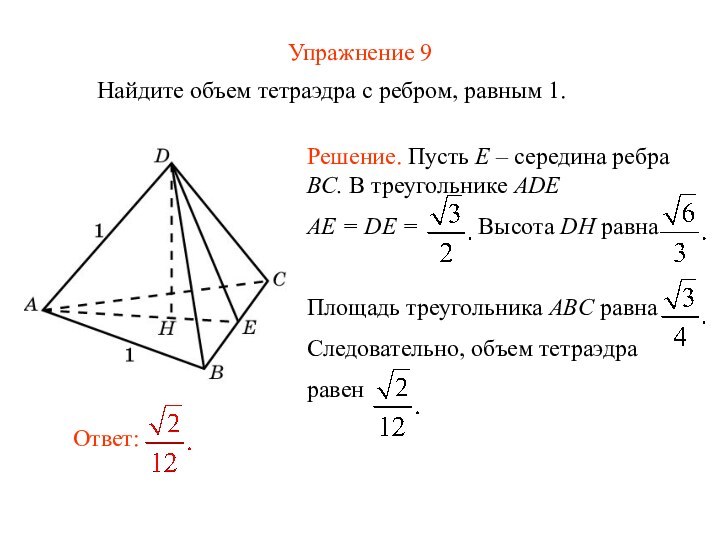
Упражнение 9
Найдите объем тетраэдра с ребром, равным 1.
Слайд 12
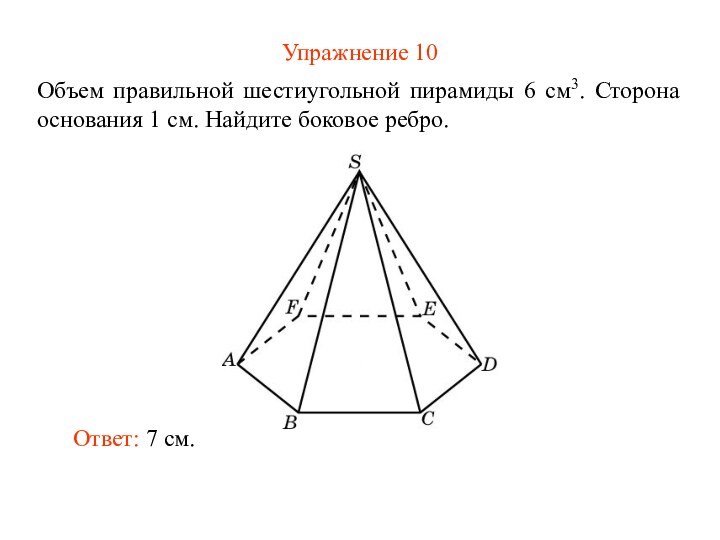
Упражнение 10
Объем правильной шестиугольной пирамиды 6 см3. Сторона
основания 1 см. Найдите боковое ребро.
Ответ: 7 см.
Слайд 13
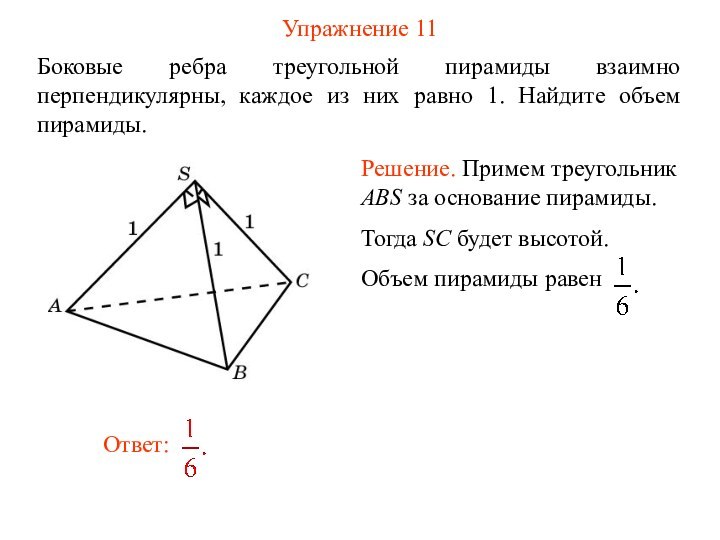
Упражнение 11
Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое
из них равно 1. Найдите объем пирамиды.
Слайд 14
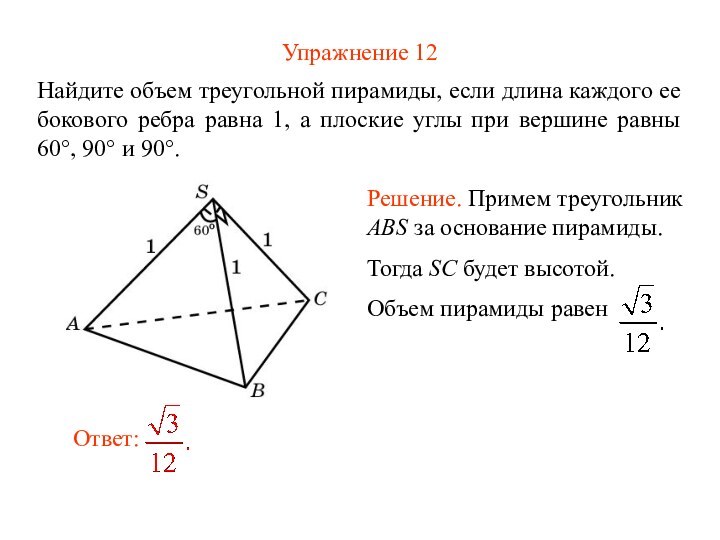
Упражнение 12
Найдите объем треугольной пирамиды, если длина каждого
ее бокового ребра равна 1, а плоские углы при
вершине равны 60°, 90° и 90°.
Слайд 15
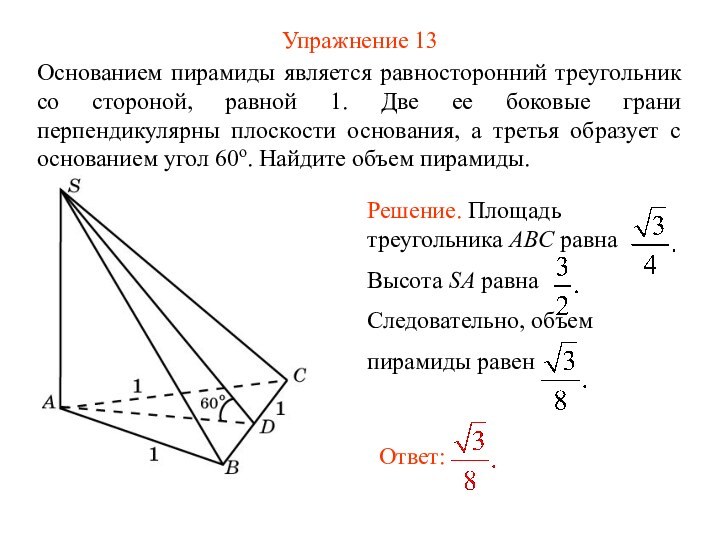
Упражнение 13
Основанием пирамиды является равносторонний треугольник со стороной,
равной 1. Две ее боковые грани перпендикулярны плоскости основания,
а третья образует с основанием угол 60о. Найдите объем пирамиды.
Слайд 16
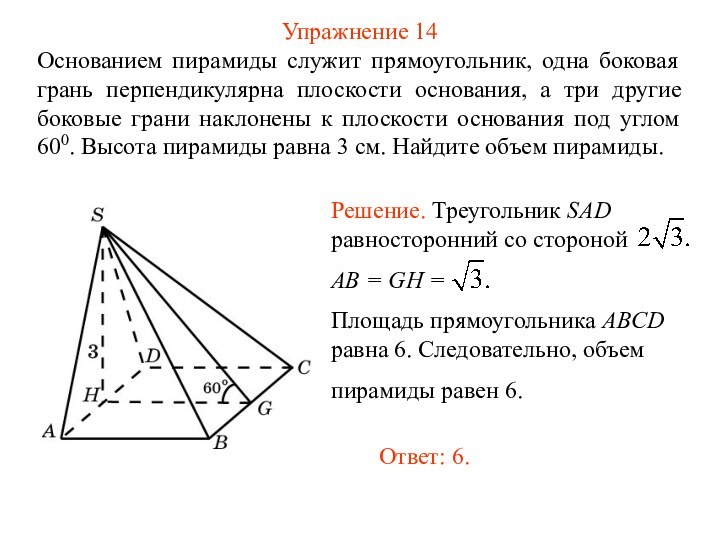
Упражнение 14
Основанием пирамиды служит прямоугольник, одна боковая грань
перпендикулярна плоскости основания, а три другие боковые грани наклонены
к плоскости основания под углом 600. Высота пирамиды равна 3 см. Найдите объем пирамиды.
Слайд 17
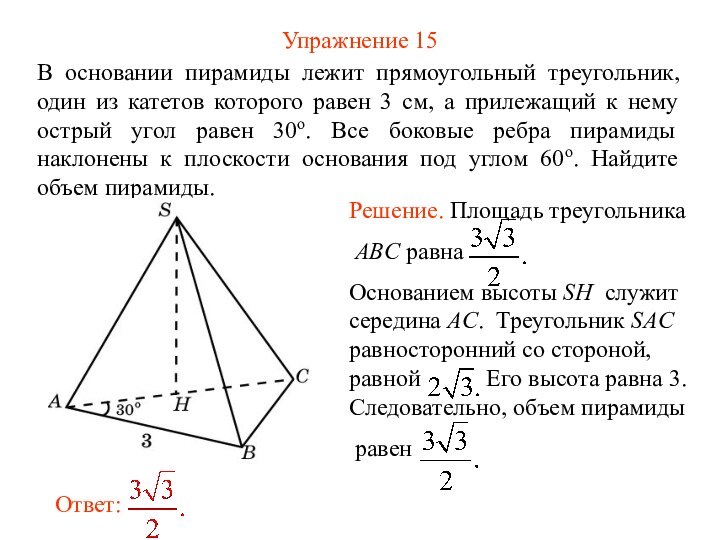
Упражнение 15
В основании пирамиды лежит прямоугольный треугольник, один
из катетов которого равен 3 см, а прилежащий к
нему острый угол равен 30о. Все боковые ребра пирамиды наклонены к плоскости основания под углом 60о. Найдите объем пирамиды.
Слайд 18
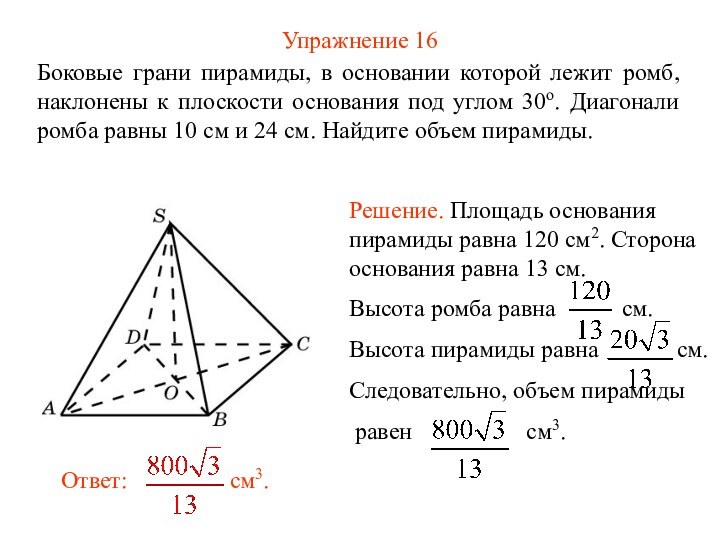
Упражнение 16
Боковые грани пирамиды, в основании которой лежит
ромб, наклонены к плоскости основания под углом 30о. Диагонали
ромба равны 10 см и 24 см. Найдите объем пирамиды.
Слайд 19
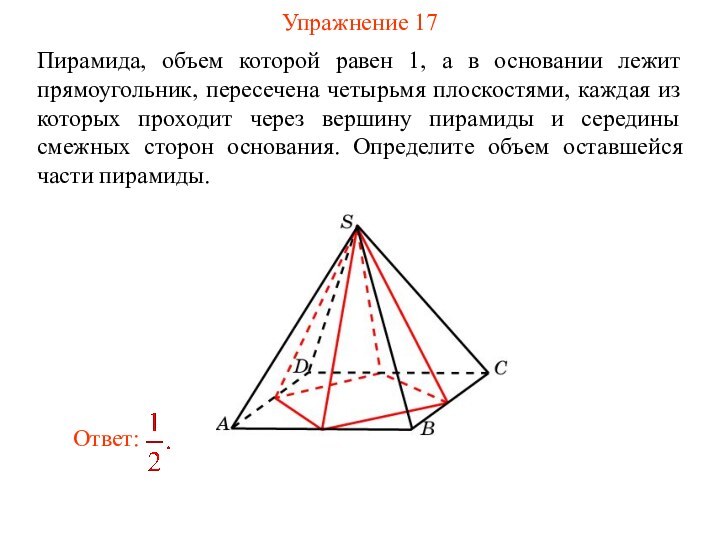
Упражнение 17
Пирамида, объем которой равен 1, а в
основании лежит прямоугольник, пересечена четырьмя плоскостями, каждая из которых
проходит через вершину пирамиды и середины смежных сторон основания. Определите объем оставшейся части пирамиды.
Слайд 20
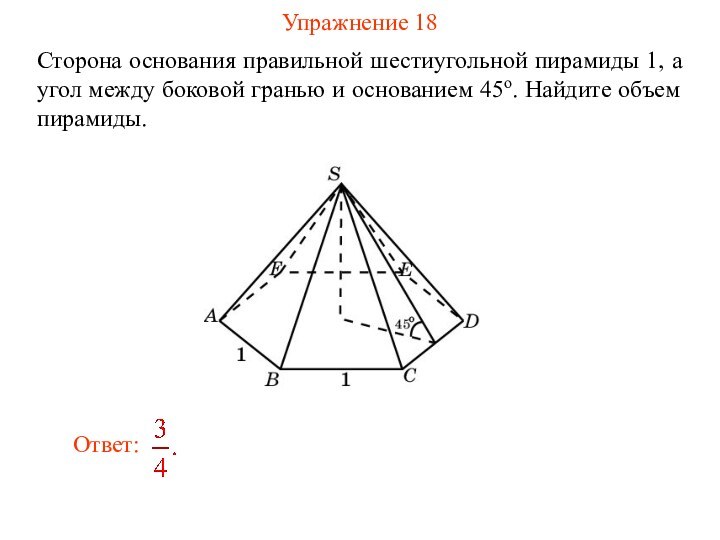
Упражнение 18
Сторона основания правильной шестиугольной пирамиды 1, а
угол между боковой гранью и основанием 45о. Найдите объем
пирамиды.
Слайд 21
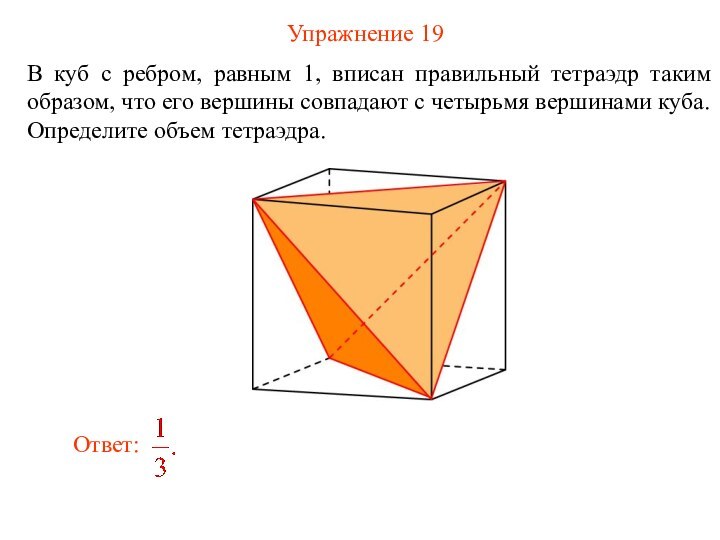
Упражнение 19
В куб с ребром, равным 1, вписан
правильный тетраэдр таким образом, что его вершины совпадают с
четырьмя вершинами куба. Определите объем тетраэдра.
Слайд 22
Упражнение 20
Развертка треугольной пирамиды представляет собой квадрат со
стороной 1. Найдите объем этой пирамиды.
Слайд 23
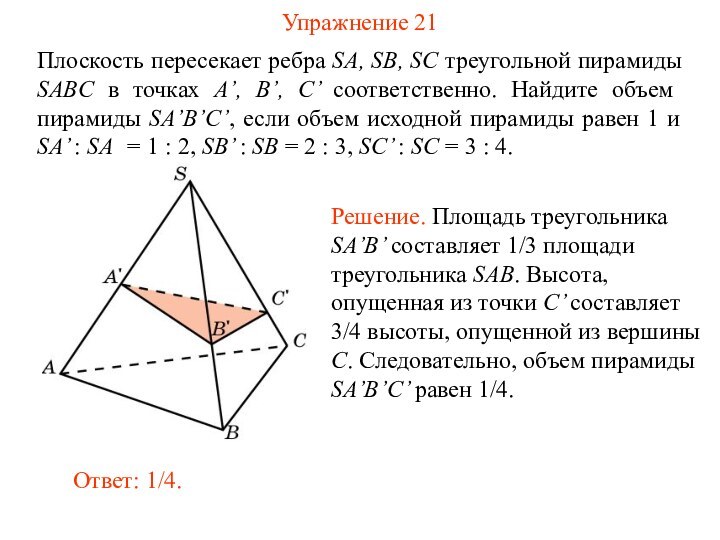
Упражнение 21
Плоскость пересекает ребра SA, SB, SC треугольной
пирамиды SABC в точках A’, B’, C’ соответственно. Найдите
объем пирамиды SA’B’C’, если объем исходной пирамиды равен 1 и SA’ : SA = 1 : 2, SB’ : SB = 2 : 3, SC’ : SC = 3 : 4.
Слайд 24
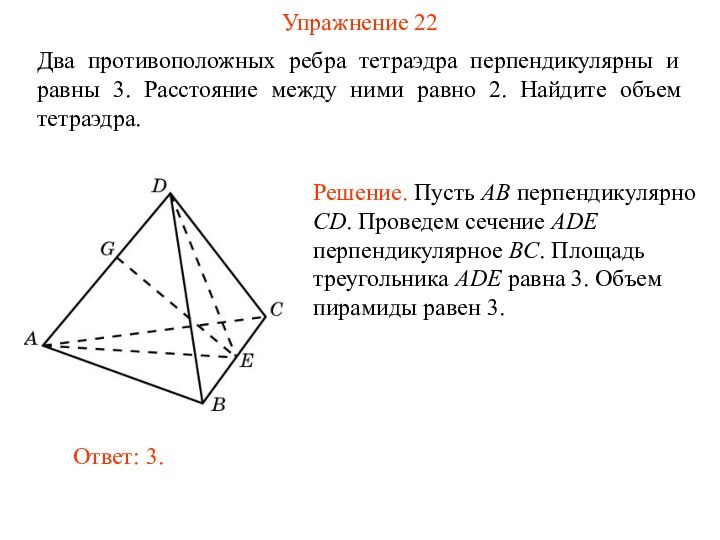
Упражнение 22
Два противоположных ребра тетраэдра перпендикулярны и равны
3. Расстояние между ними равно 2. Найдите объем тетраэдра.
Слайд 25
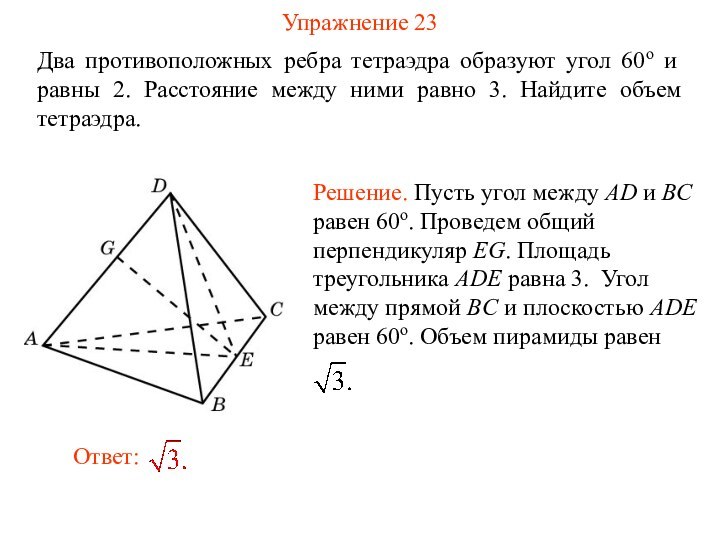
Упражнение 23
Два противоположных ребра тетраэдра образуют угол 60о
и равны 2. Расстояние между ними равно 3. Найдите
объем тетраэдра.
Слайд 26
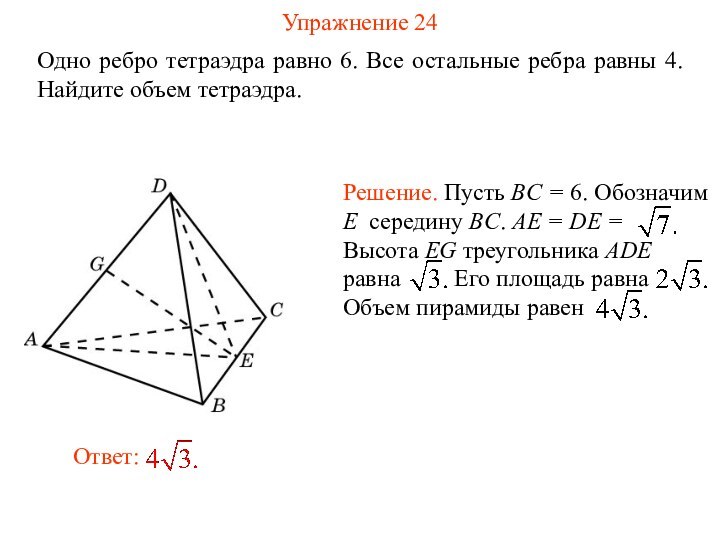
Упражнение 24
Одно ребро тетраэдра равно 6. Все остальные
ребра равны 4. Найдите объем тетраэдра.
Слайд 27
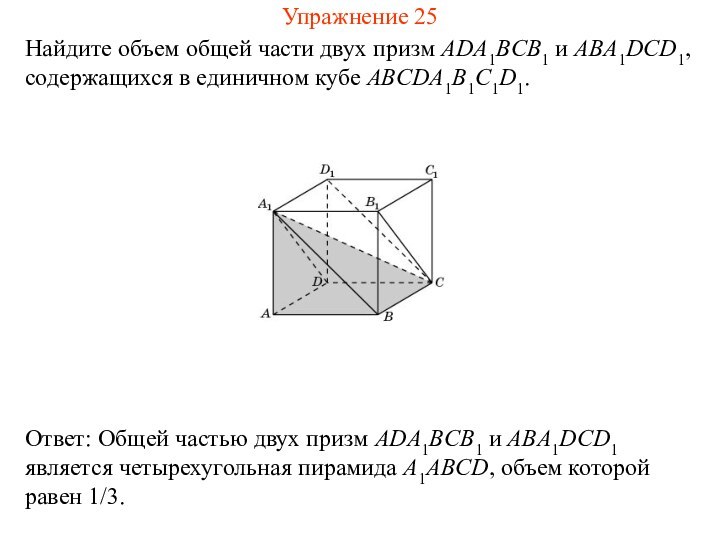
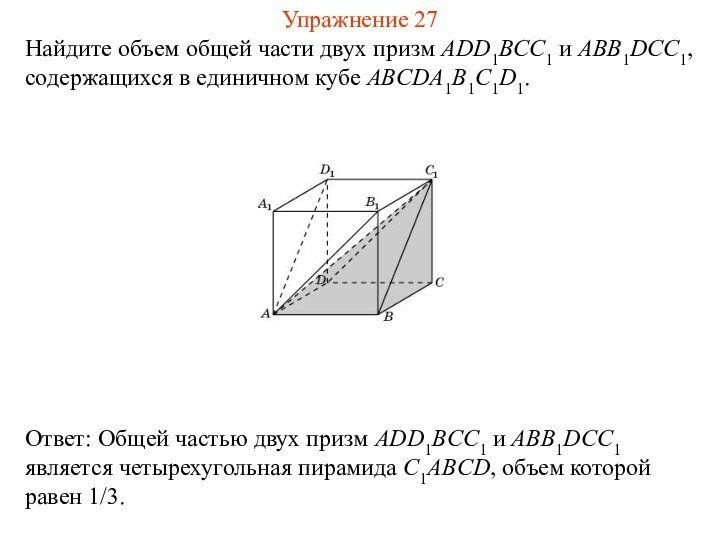
Найдите объем общей части двух призм ADA1BCB1 и
ABA1DCD1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 25
Слайд 28
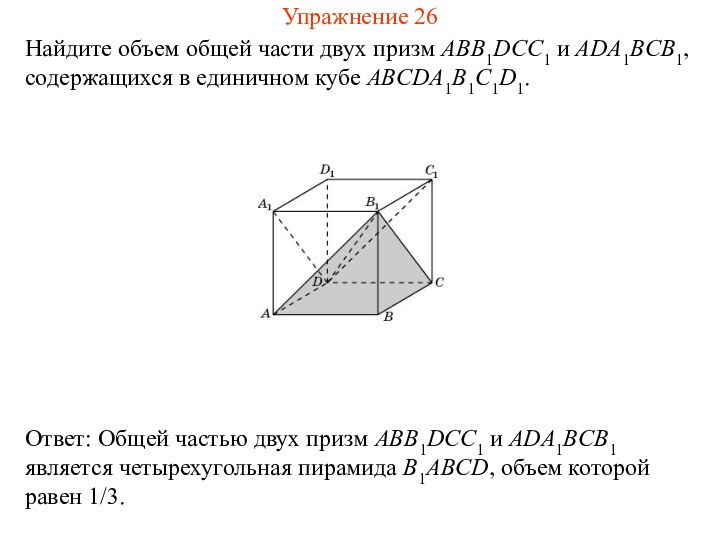
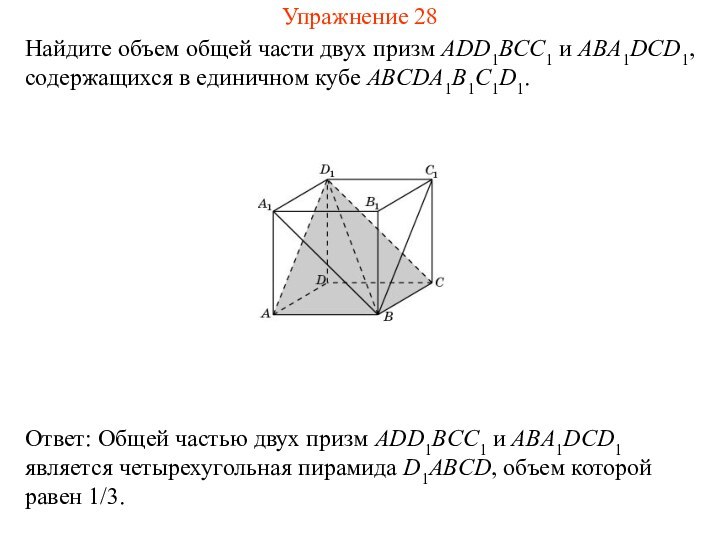
Найдите объем общей части двух призм ABB1DCC1 и
ADA1BCB1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 26
Слайд 29
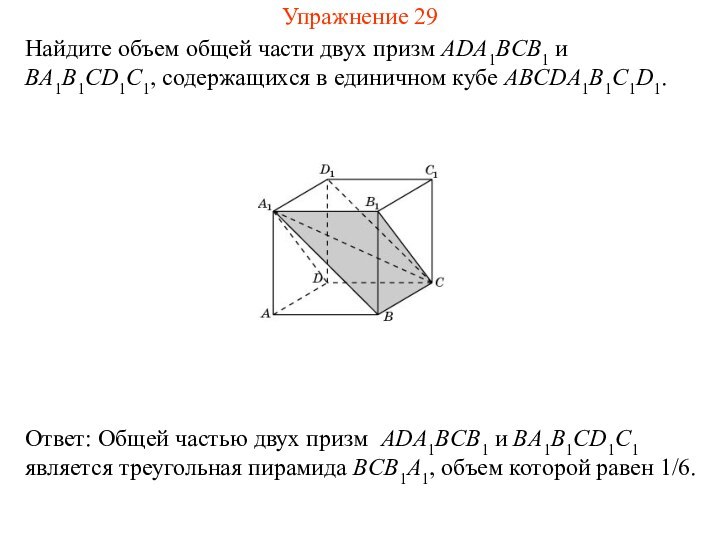
Найдите объем общей части двух призм ADD1BCC1 и
ABB1DCC1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 27
Слайд 30
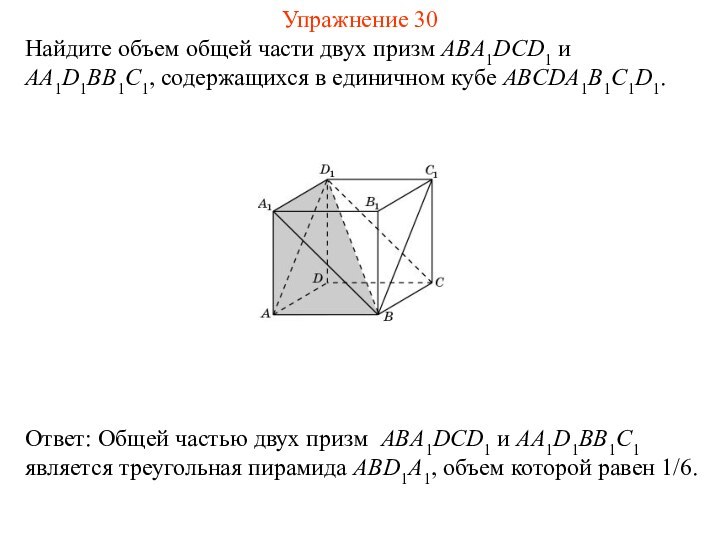
Найдите объем общей части двух призм ADD1BCC1 и
ABA1DCD1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 28
Слайд 31
Найдите объем общей части двух призм ADA1BCB1 и
BA1B1CD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 29
Слайд 32
Найдите объем общей части двух призм ABA1DCD1 и
AA1D1BB1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 30
Слайд 33
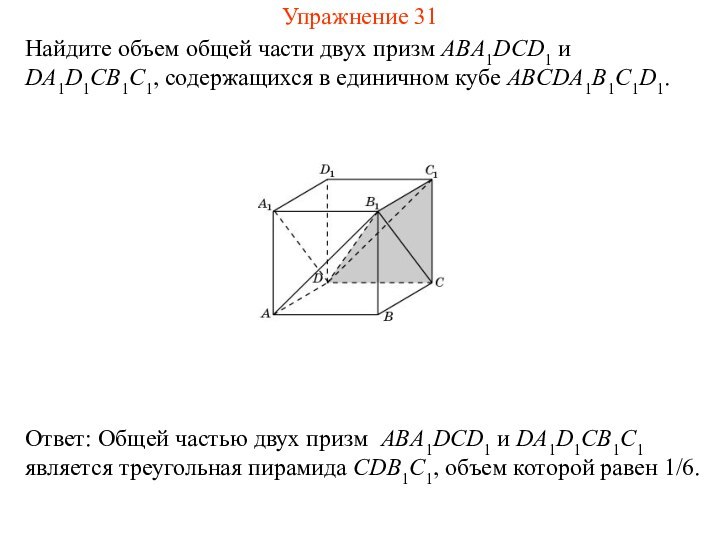
Найдите объем общей части двух призм ABA1DCD1 и
DA1D1CB1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 31
Слайд 34
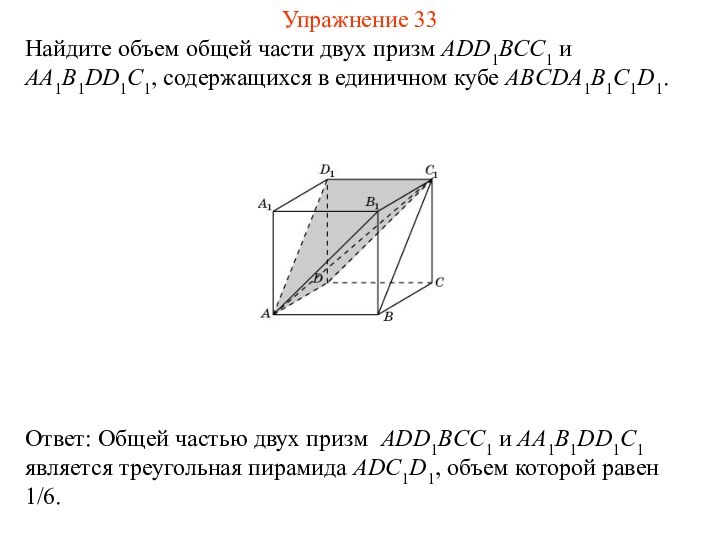
Найдите объем общей части двух призм ADD1BCC1 и
AA1B1DD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 33
Слайд 35
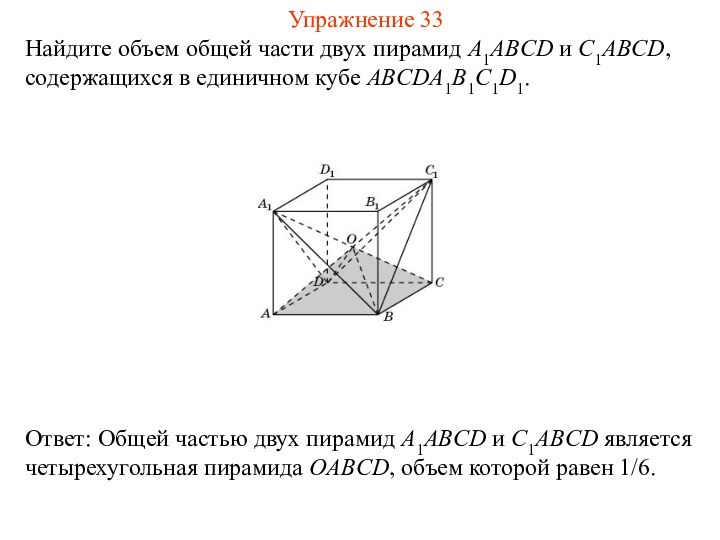
Найдите объем общей части двух пирамид A1ABCD и
C1ABCD, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 33
Слайд 36
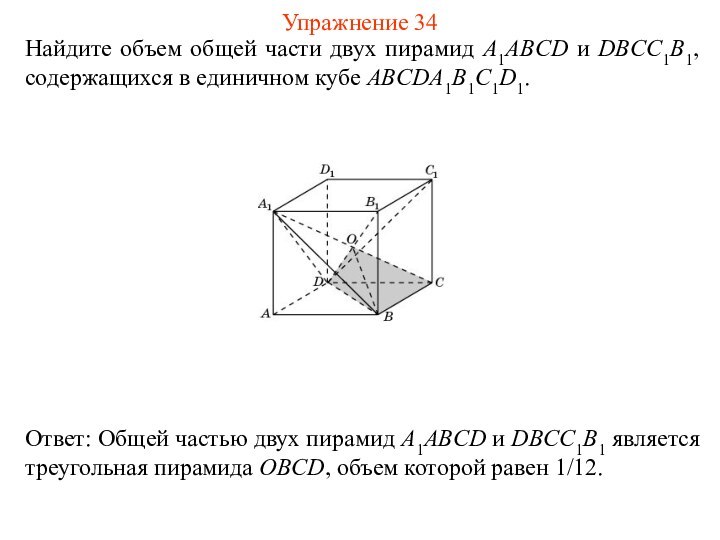
Найдите объем общей части двух пирамид A1ABCD и
DBCC1B1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 34
Слайд 37
Найдите объем общей части двух пирамид A1ABCD и
ABCC1B1, содержащихся в единичном кубе ABCDA1B1C1D1.
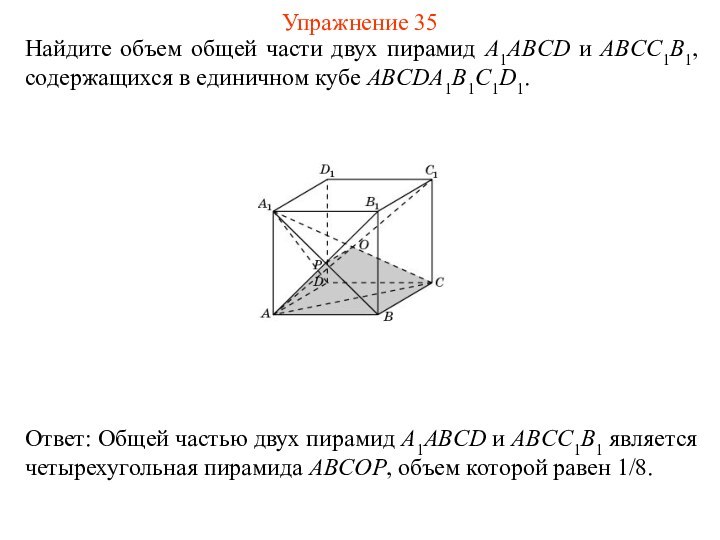
Упражнение 35
Слайд 38
Найдите объем общей части двух пирамид A1ABCD и
BCDD1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
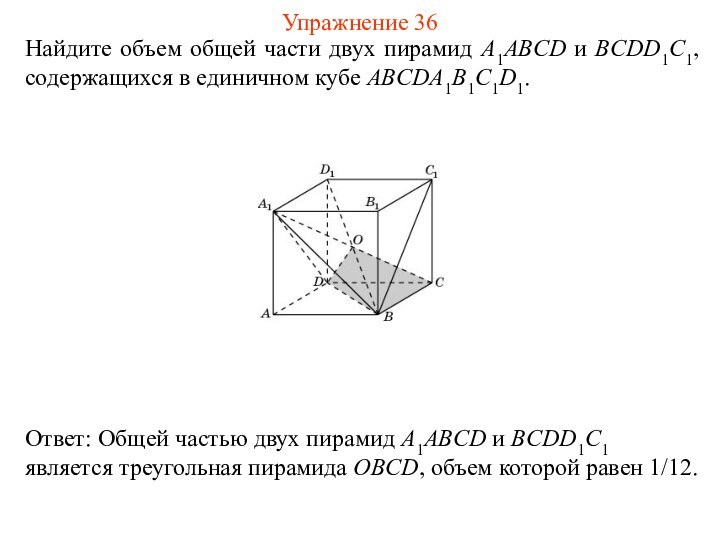
Упражнение 36
Слайд 39
Найдите объем общей части двух пирамид A1ABCD и
CADD1A1, содержащихся в единичном кубе ABCDA1B1C1D1.
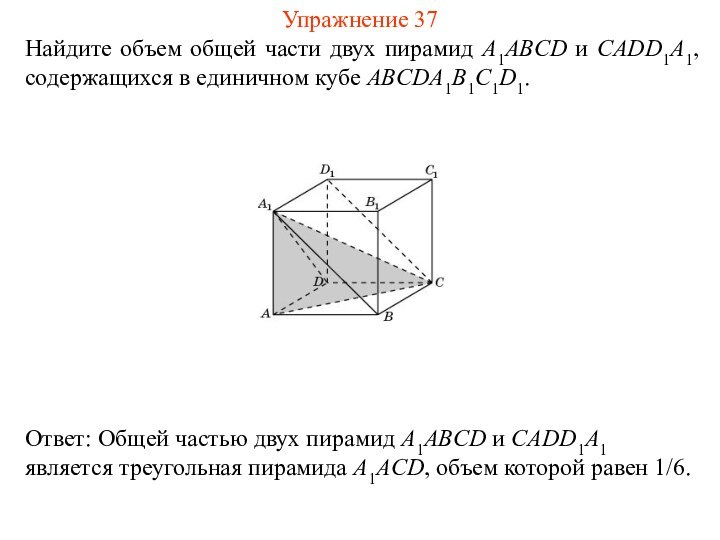
Упражнение 37
Слайд 40
Найдите объем общей части двух пирамид A1ABCD и
B1ADD1A1, содержащихся в единичном кубе ABCDA1B1C1D1.
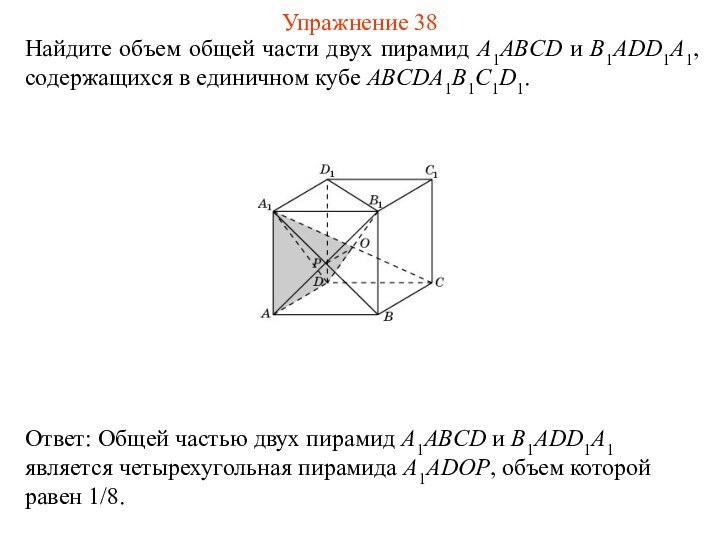
Упражнение 38
Слайд 41
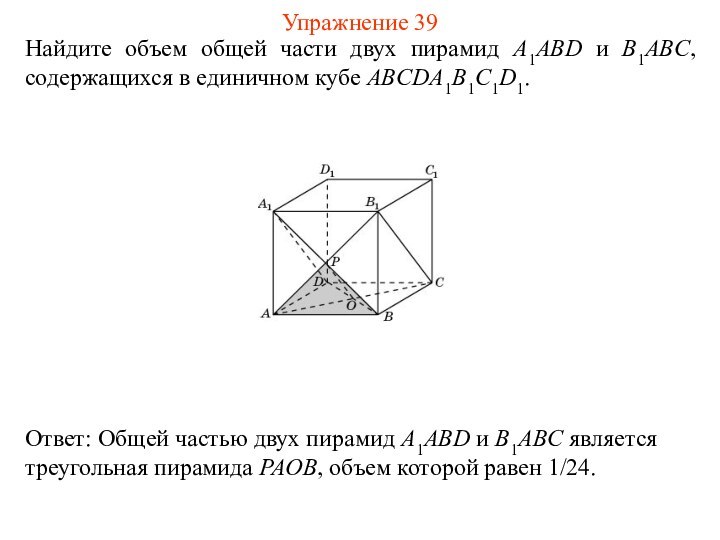
Найдите объем общей части двух пирамид A1ABD и
B1ABC, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 39
Слайд 42
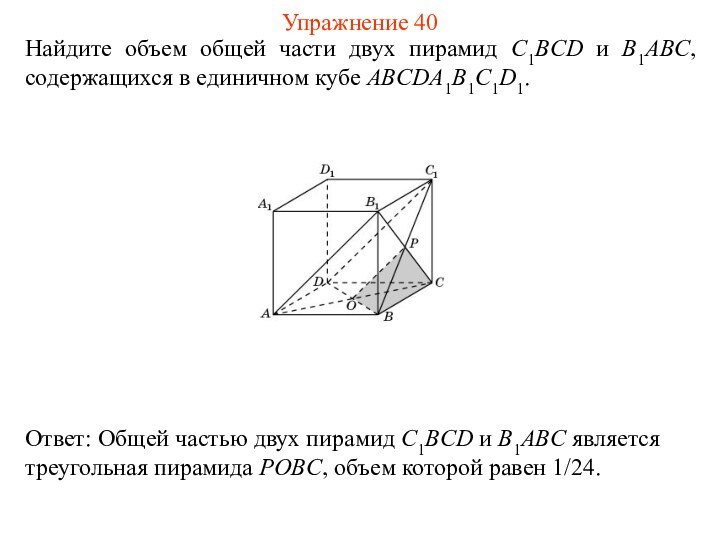
Найдите объем общей части двух пирамид C1BCD и
B1ABC, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 40
Слайд 43
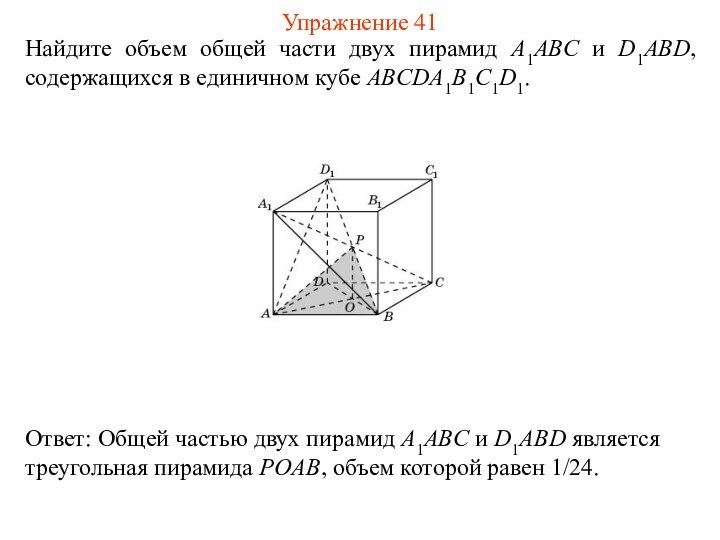
Найдите объем общей части двух пирамид A1ABC и
D1ABD, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 41
Слайд 44
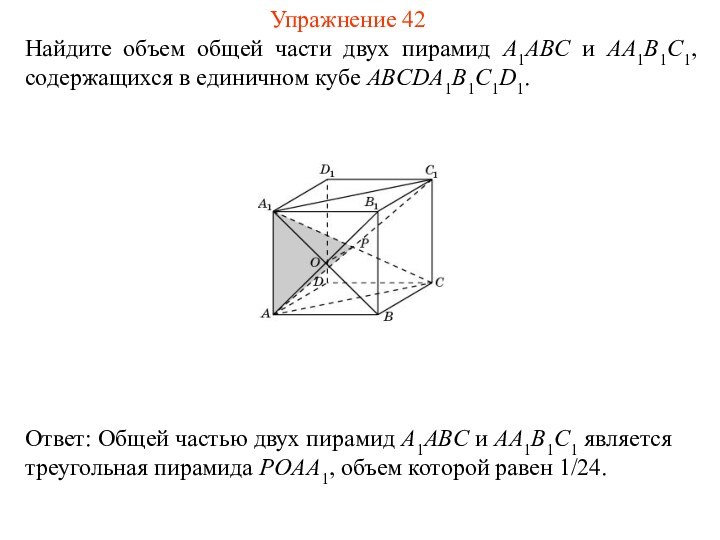
Найдите объем общей части двух пирамид A1ABC и
AA1B1C1, содержащихся в единичном кубе ABCDA1B1C1D1.
Упражнение 42
Слайд 45
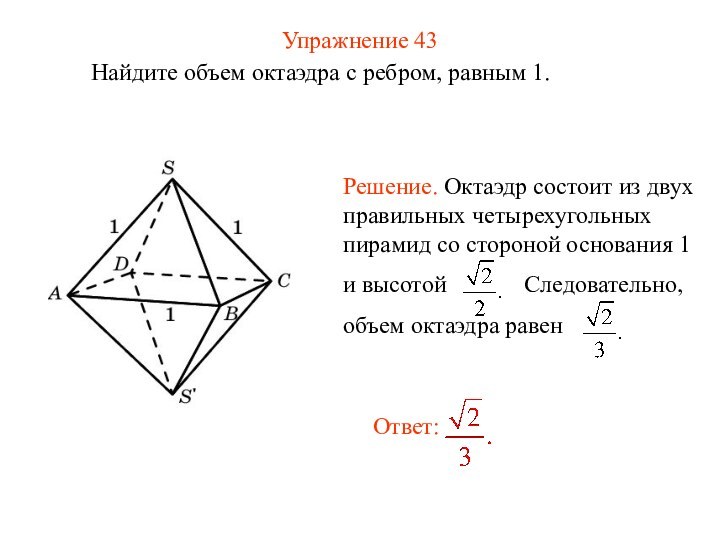
Упражнение 43
Найдите объем октаэдра с ребром, равным 1.
Слайд 46
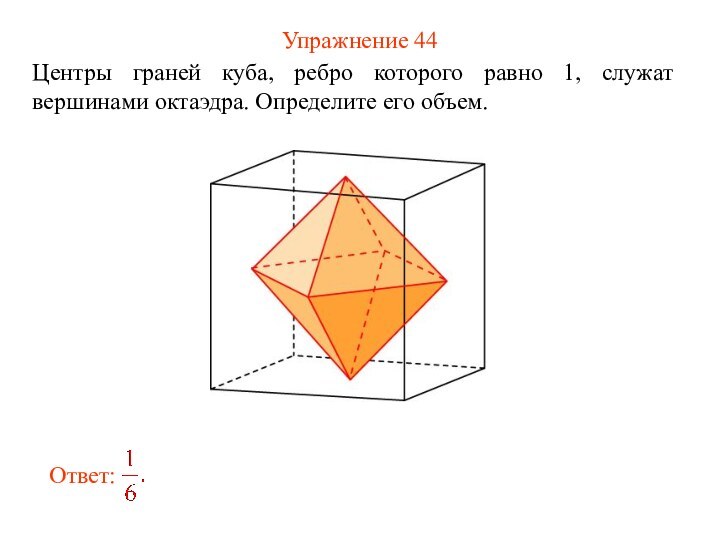
Упражнение 44
Центры граней куба, ребро которого равно 1,
служат вершинами октаэдра. Определите его объем.
Слайд 47
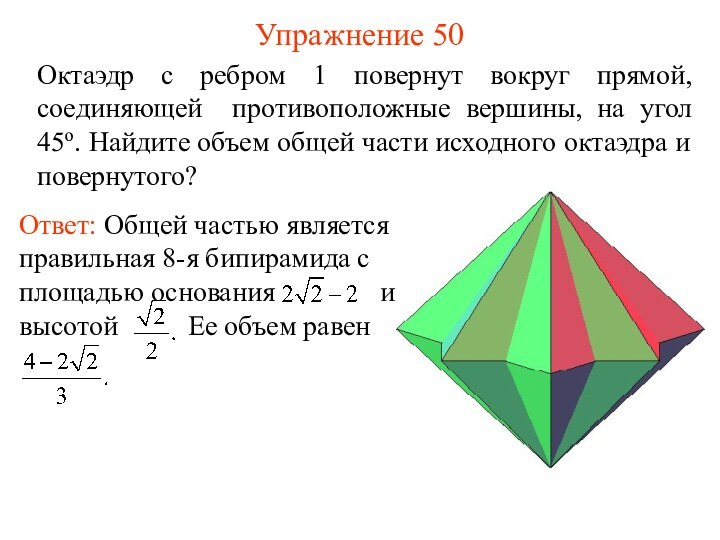
Упражнение 45
Два куба с ребром a имеют общую
диагональ, но один повернут вокруг этой диагонали на угол
60° по отношению к другому. Найдите объем их общей части.
Слайд 48
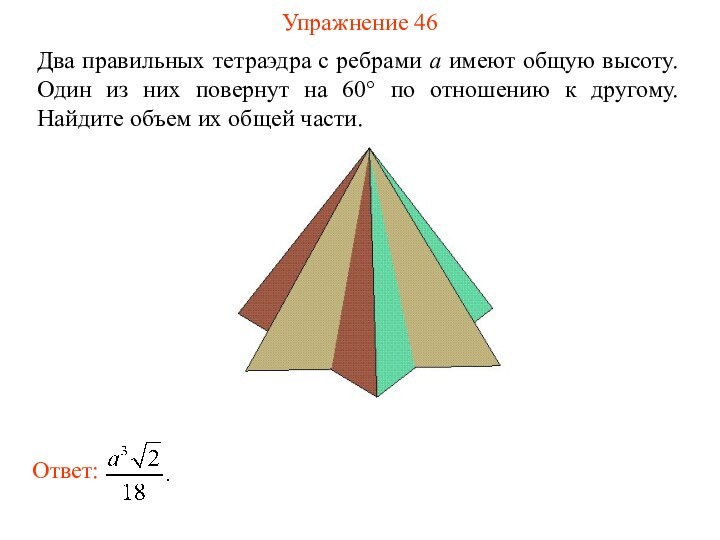
Упражнение 46
Два правильных тетраэдра с ребрами a имеют
общую высоту. Один из них повернут на 60° по
отношению к другому. Найдите объем их общей части.
Слайд 49
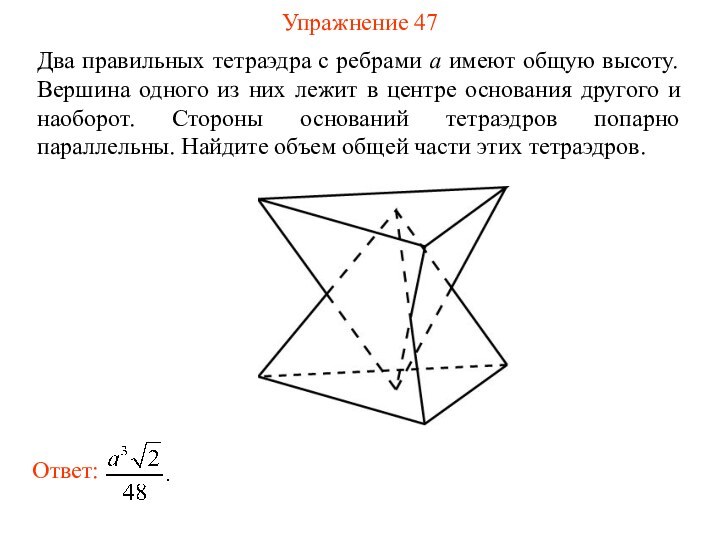
Упражнение 47
Два правильных тетраэдра с ребрами a имеют
общую высоту. Вершина одного из них лежит в центре
основания другого и наоборот. Стороны оснований тетраэдров попарно параллельны. Найдите объем общей части этих тетраэдров.
Слайд 50
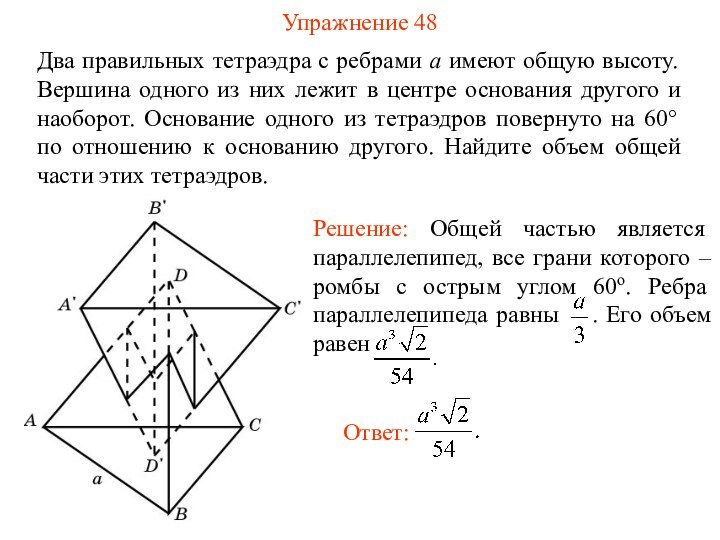
Упражнение 48
Два правильных тетраэдра с ребрами a имеют
общую высоту. Вершина одного из них лежит в центре
основания другого и наоборот. Основание одного из тетраэдров повернуто на 60° по отношению к основанию другого. Найдите объем общей части этих тетраэдров.
Слайд 51
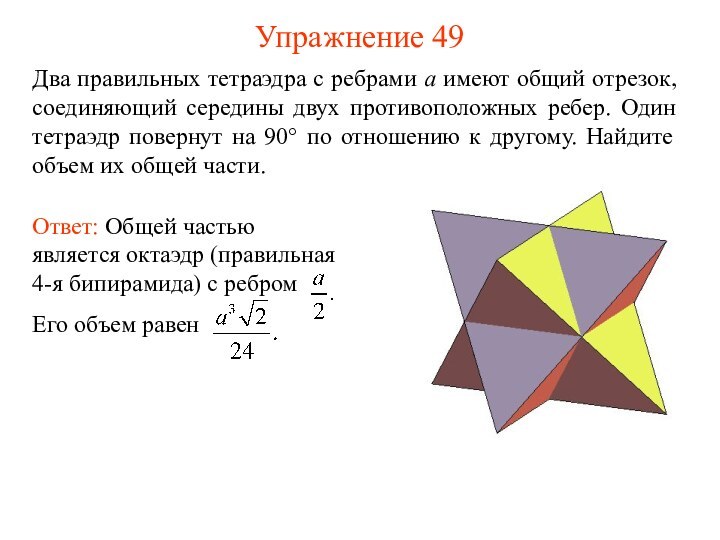
Упражнение 49
Два правильных тетраэдра с ребрами a имеют
общий отрезок, соединяющий середины двух противоположных ребер. Один тетраэдр
повернут на 90° по отношению к другому. Найдите объем их общей части.