- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Мультимедийная презентация для сопровождения занятий по геометрии 11 класса по теме Многогранники
Содержание
- 2. Многогранники10 класс
- 3. Цель урокаПознакомить учащихся с различными видами многогранников. Показать связь геометрии и природы.
- 4. План урокаОрганизационный момент. Усвоение нового материала (работа
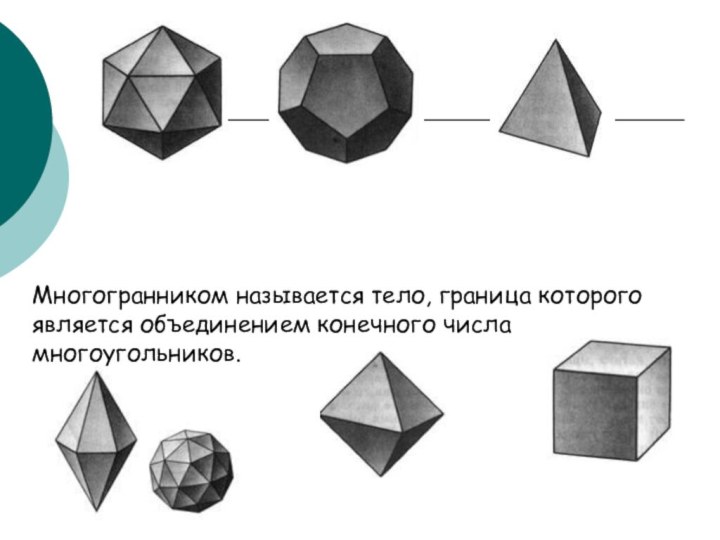
- 5. Многогранником называется тело, граница которого является объединением конечного числа многоугольников.
- 6. Многогранники выпуклыеневыпуклыеТелаАрхимедаТела ПлатонаТела Кеплера-Пуансо
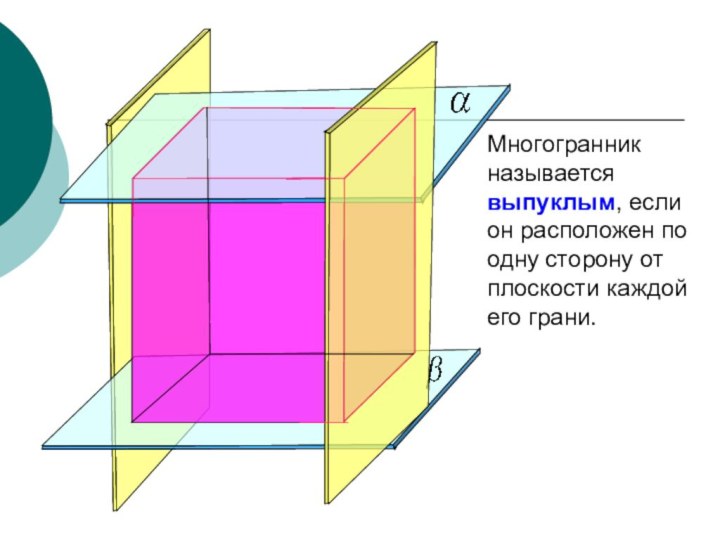
- 7. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
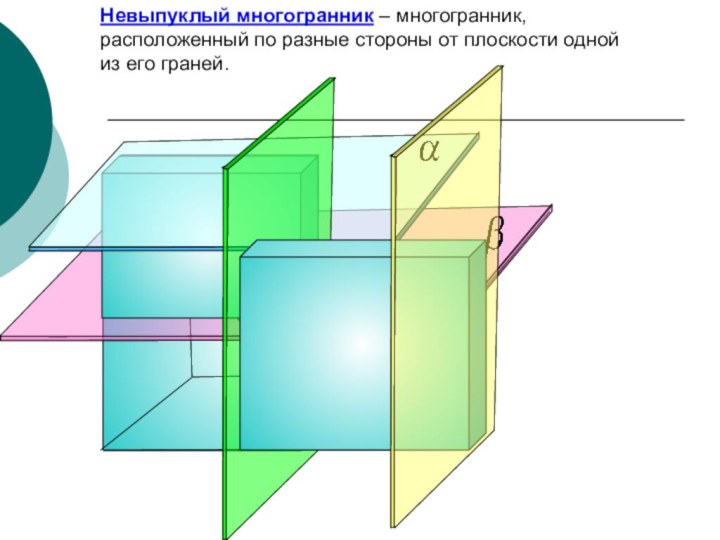
- 8. Невыпуклый многогранник – многогранник, расположенный по разные стороны от плоскости одной из его граней.
- 9. Правильными многогранниками называют выпуклые многогранники, все грани
- 10. Правильные многогранники Сколько же их существует?
- 11. ТетраэдрСначала рассмотрим случай, когда грани многогранника -
- 12. Октаэдр-Если добавить к развертке вершины еще один
- 13. ИкосаэдрДобавление пятого треугольника даст угол 300° -
- 14. Если же добавить еще один, шестой треугольник,
- 15. Куб или правильный гексаэдрТеперь перейдем к квадратным
- 16. Додекаэдр-Три пятиугольные грани дают угол развертки 3*108°=324
- 17. Для шестиугольников уже три грани дают угол
- 18. Сделаем вывод: Мы убедились, что существует лишь
- 19. ТетраэдрИкосаэдрГексаэдрДодекаэдрОктаэдр
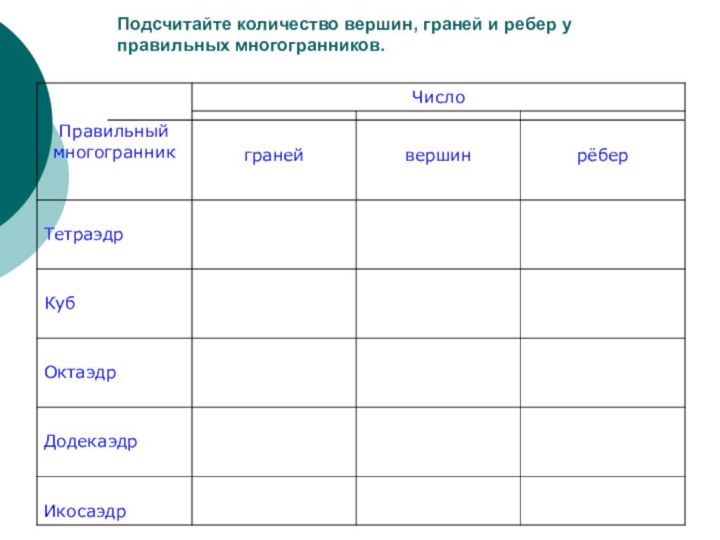
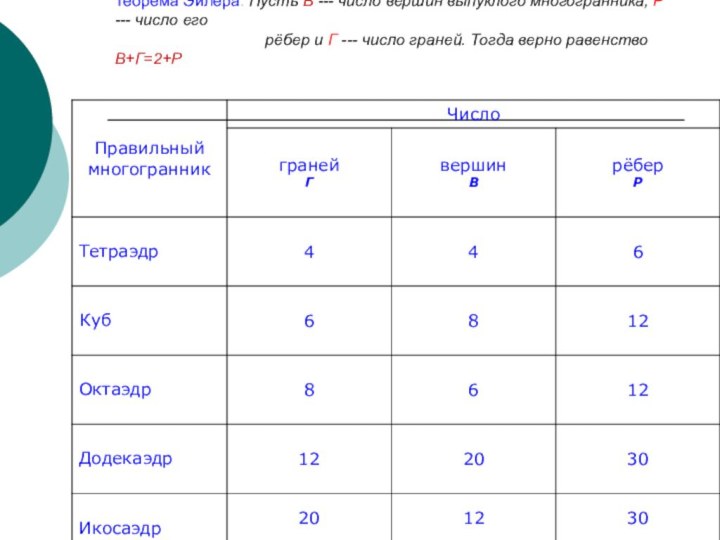
- 20. Подсчитайте количество вершин, граней и ребер у правильных многогранников.
- 21. Теорема Эйлера. Пусть В --- число вершин
- 22. Эти тела еще называют телами ПлатонаПлатон связал с этими телами формы атомов основных стихий природы.
- 23. огонь тетраэдрвода икосаэдр воздух октаэдр земля гексаэдр вселенная додекаэдр стихии
- 24. Тела АрхимедаАрхимедовыми телами называются полуправильные однородные выпуклые
- 25. Тела Архимеда
- 26. Тела Кеплера - ПуансоСреди невыпуклых однородных многогранников
- 27. Большой звездчатыйдодекаэдрБольшой икосаэдрМалый звездчатыйдодекаэдр
- 28. Многогранники в архитектуреВеликая пирамида в Гизе. Эта
- 30. Александрийский маяк. Маяк был построен на маленьком
- 31. Три башниФаросский маяк состоял из трех мраморных
- 32. Многогранники в искусствеЗнаменитый художник, увлекавшийся геометрией, Альбрехт
- 33. Сальвадор Дали на картине «Тайная вечеря» изобразил
- 34. Многогранники в природеПравильные многогранники – самые выгодные
- 35. Пчёлы строили
- 36. Икосаэдр оказался в центревнимания биологов в их мнениях относительно формы вирусов.
- 37. Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр.
- 38. А теперь проверьте свои знания по изученному материалу
- 39. Тестирование.
- 40. 1. Поверхность, составленная из четырех треугольниковА) ТЕТРАЭДРС) КВАДРАТB) ПАРАЛЛЕЛЕПИПЕДD) ШАР
- 41. 2. Поверхность, составленная из многоугольников и ограничива- ющая некоторое геометрическое телоА) МНОГОУГОЛЬНИКС) ТРЕУГОЛЬНИКB) МНОГОГРАННИКD) КВАДРАТ
- 42. 3. Многоугольник, из которого составлен многогранникА) СТОРОНАС) ГРАНЬB) РЕБРОD) ВЕРШИНА
- 43. 4. Отрезок, соединяющий две вершины, не принадлежащие одной граниА) ДИАГОНАЛЬС) ВЫСОТАB) МЕДИАНАD) АПОФЕМА
- 44. 5. Высота боковой грани правильной пирамиды, проведенная из ее вершины А) ДИАГОНАЛЬС) КАТЕТB) АПОФЕМАD) ГИПОТЕНУЗА
- 45. 6. Этот правильный многогранник составлен из 8-ми равносторонних треугольников А) КВАДРАТС) ДОДЕКАЭДРB) ТЕТРАЭДРD) ОКТАЭДР
- 46. 7. Составлен из 6-ти правильных четырехугольников А) КВАДРАТС) КУБB) ТЕТРАЭДРD) ПИРАМИДА
- 47. 8. Стихия тетраэдра А) ВОДАС) ЗЕМЛЯB) ВОЗДУХD) ОГОНЬ
- 48. 9. Многоугольник, подобный пчелиным сотамА) 8-МИ УГОЛЬНИКС) 4-Х УГОЛЬНИКB) 6-ТИ УГОЛЬНИКD) ТРЕУГОЛЬНИК
- 49. Проверь себя.1. A2. B3. C4. A5. B6. D7. C8. D9. B
- 50. Скачать презентацию
- 51. Похожие презентации
Многогранники10 класс
Слайд 3
Цель урока
Познакомить учащихся с различными видами многогранников.
Показать
связь геометрии и природы.
Слайд 4
План урока
Организационный момент.
Усвоение нового материала (работа с
презентацией и объяснение материала учителем)
Закрепление новых знаний
Решение задач.
Подведение итога урока.
Домашнее задание.
Слайд 5 Многогранником называется тело, граница которого является объединением конечного
числа многоугольников.
Слайд 7
Многогранник называется выпуклым, если он расположен по одну
сторону от плоскости каждой его грани.
Слайд 8
Невыпуклый многогранник – многогранник, расположенный по разные стороны
от плоскости одной из его граней.
Слайд 9
Правильными многогранниками
называют выпуклые многогранники, все грани и
все углы которых равны, причем грани - правильные многоугольники.
Слайд 11
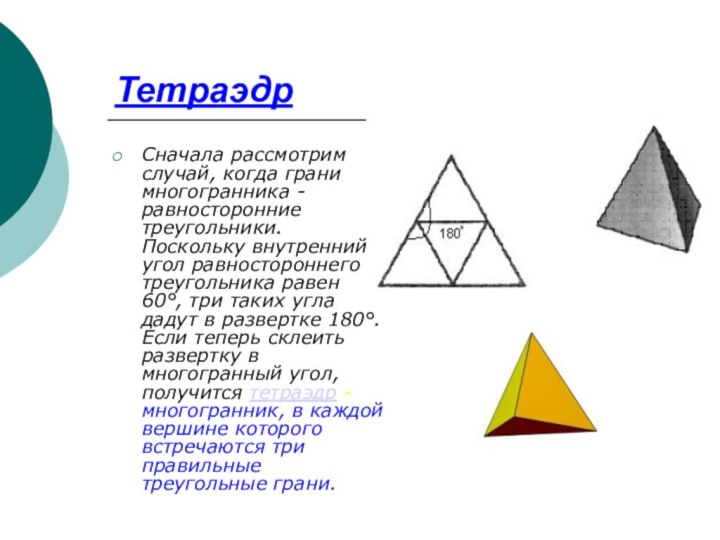
Тетраэдр
Сначала рассмотрим случай, когда грани многогранника - равносторонние
треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три
таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани.
Слайд 12
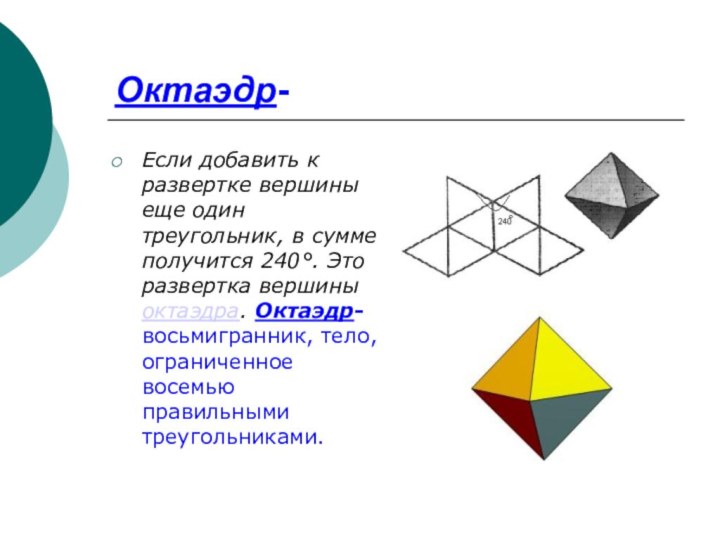
Октаэдр-
Если добавить к развертке вершины еще один треугольник,
в сумме получится 240°. Это развертка вершины октаэдра. Октаэдр-восьмигранник,
тело, ограниченное восемью правильными треугольниками.
Слайд 13
Икосаэдр
Добавление пятого треугольника даст угол 300° - мы
получаем развертку вершины икосаэдра.
Икосаэдр-двадцатигранник, тело, ограниченное двадцатью равносторонними треугольниками
Слайд 14 Если же добавить еще один, шестой треугольник, сумма
углов станет равной 360° - эта развертка, очевидно, не
может соответствовать ни одному выпуклому многограннику.
Слайд 15
Куб или правильный гексаэдр
Теперь перейдем к квадратным граням.
Развертка из трех квадратных граней имеет угол 3x90°=270° -
получается вершина куба, который также называют гексаэдром. Добавление еще одного квадрата увеличит угол до 360° - этой развертке уже не соответствует никакой выпуклый многогранник.Куб или правильный гексаэдр - правильная четырехугольная призма с равными ребрами, ограниченная шестью квадратами.
Слайд 16
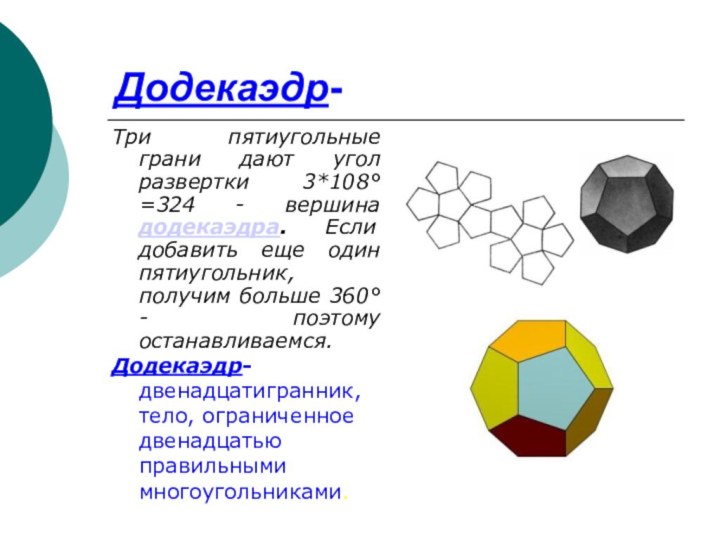
Додекаэдр-
Три пятиугольные грани дают угол развертки 3*108°=324 -
вершина додекаэдра. Если добавить еще один пятиугольник, получим больше
360° - поэтому останавливаемся.Додекаэдр-двенадцатигранник, тело, ограниченное двенадцатью правильными многоугольниками.
Слайд 17 Для шестиугольников уже три грани дают угол развертки
3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не
существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
Слайд 18
Сделаем вывод:
Мы убедились, что существует лишь пять выпуклых
правильных многогранников - тетраэдр, октаэдр и икосаэдр с треугольными
гранями, куб (гексаэдр) с квадратными гранями и додекаэдр с пятиугольными гранями. Названия этих многогранников пришли из Древней Греции, и в них указывается число граней:«эдра» - грань
«тетра» - 4
«гекса» - 6
«окта» - 8
«икоса» - 20
«додека» - 12
Слайд 21 Теорема Эйлера. Пусть В --- число вершин выпуклого
многогранника, Р --- число его
рёбер и Г --- число граней. Тогда верно равенство В+Г=2+Р
Слайд 22
Эти тела еще называют телами Платона
Платон связал с
этими телами формы атомов основных стихий природы.
Слайд 24
Тела Архимеда
Архимедовыми телами называются полуправильные однородные выпуклые многогранники,
то есть выпуклые многогранники, все многогранные углы которых равны,
а грани - правильные многоугольники нескольких типов.
Слайд 26
Тела
Кеплера - Пуансо
Среди невыпуклых однородных многогранников существуют
аналоги платоновых тел - четыре правильных невыпуклых однородных многогранника
или тела Кеплера - Пуансо.Как следует из их названия, тела Кеплера-Пуансо - это невыпуклые однородные многогранники, все грани которых - одинаковые правильные многоугольники, и все многогранные углы которых равны. Грани при этом могут быть как выпуклыми, так и невыпуклыми.
Слайд 28
Многогранники в архитектуре
Великая пирамида в Гизе. Эта грандиозная
Египетская пирамида является древнейшим из Семи чудес древности.
Великая пирамида была построена как гробница Хуфу, известного грекам как Хеопс. Он был одним из фараонов, или царей древнего Египта, а его гробница была завершена в 2580 году до н.э. Позднее в Гизе было построено еще две пирамиды, для сына и внука Хуфу, а также меньшие по размерам пирамиды для их цариц.
Слайд 30
Александрийский маяк.
Маяк был построен на маленьком острове
Фарос в Средиземном море, около берегов Александрии. Этот оживленный
порт основал Александр Великий во время посещения Египта. Сооружение назвали по имени острова. На его строительство, должно быть, ушло 20 лет, а завершен он был около 280 г. до н.э., во времена правления Птолемея II, царя Египта.
Слайд 31
Три башни
Фаросский маяк состоял из трех мраморных башен,
стоявших на основании из массивных каменных блоков. Первая башня
была прямоугольной, в ней находились комнаты, в которых жили рабочие и солдаты. Над этой башней располагалась меньшая, восьмиугольная башня со спиральным пандусом, ведущим в верхнюю башню.
Слайд 32
Многогранники в искусстве
Знаменитый художник, увлекавшийся геометрией, Альбрехт Дюрер
(1471- 1528) , в известной гравюре ''Меланхолия '‘ на
переднем плане изобразил додекаэдр.
Слайд 33
Сальвадор Дали на картине «Тайная вечеря» изобразил
И.
Христа со своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 34
Многогранники в природе
Правильные многогранники – самые выгодные фигуры.
И природа этим широко пользуется. Подтверждением тому служит форма
некоторых кристаллов.Кристалл сульфата меди II
Кристалл алюмокалиевых
квасцов
Кристалл сульфата никеля II
Слайд 37 Правильные многогранники встречаются в живой природе. Например, скелет
одноклеточного организма феодарии по форме напоминает икосаэдр.
Слайд 40
1. Поверхность, составленная из четырех треугольников
А) ТЕТРАЭДР
С) КВАДРАТ
B)
ПАРАЛЛЕЛЕПИПЕД
D) ШАР
Слайд 41 2. Поверхность, составленная из многоугольников и ограничива- ющая
некоторое геометрическое тело
А) МНОГОУГОЛЬНИК
С) ТРЕУГОЛЬНИК
B) МНОГОГРАННИК
D) КВАДРАТ
Слайд 43 4. Отрезок, соединяющий две вершины, не принадлежащие одной
грани
А) ДИАГОНАЛЬ
С) ВЫСОТА
B) МЕДИАНА
D) АПОФЕМА
Слайд 44 5. Высота боковой грани правильной пирамиды, проведенная из
ее вершины
А) ДИАГОНАЛЬ
С) КАТЕТ
B) АПОФЕМА
D) ГИПОТЕНУЗА
Слайд 45 6. Этот правильный многогранник составлен из 8-ми равносторонних
треугольников
А) КВАДРАТ
С) ДОДЕКАЭДР
B) ТЕТРАЭДР
D) ОКТАЭДР
Слайд 48
9. Многоугольник, подобный пчелиным сотам
А) 8-МИ УГОЛЬНИК
С) 4-Х
