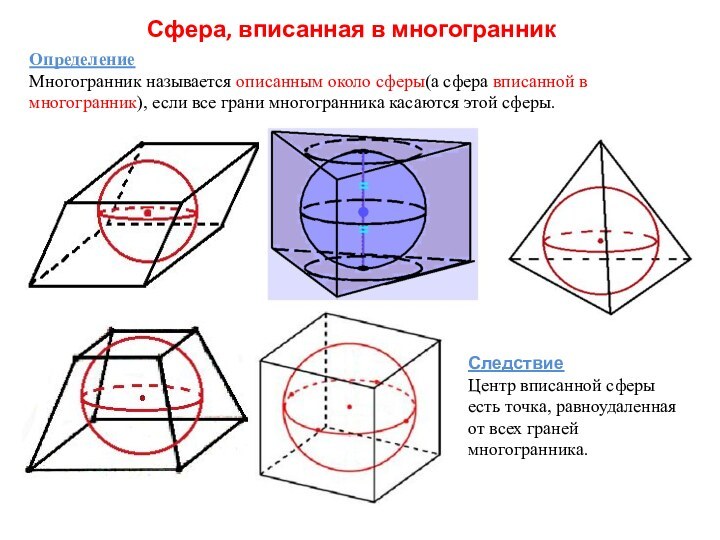
сферы(а сфера вписанной в многогранник), если все грани многогранника
касаются этой сферы.Следствие
Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сфера вписанная в многогранник
Содержание
- 2. Сфера, вписанная в многогранникОпределение Многогранник называется описанным
- 3. Подготовительные задачи1. Где расположено множество точек пространства
- 4. Теорема 2 Множество точек, равноудаленных от граней
- 5. Теорема 3Множество точек, равноудаленных от граней трехгранного
- 6. Сфера, вписанная в призмуТеорема 4В призму
- 7. 2. Расстояние между боковыми ребрами треугольной призмы
- 8. Сфера, вписанная в пирамидуБоковые грани пирамиды одинаково
- 9. 3.Основание пирамиды- треугольник со сторонами 9,10 и
- 10. Теорема 6В любой тетраэд можно вписать сферу.Теорема
- 11. 4. Шар вписан в прямую призму, основание
- 12. Скачать презентацию
- 13. Похожие презентации
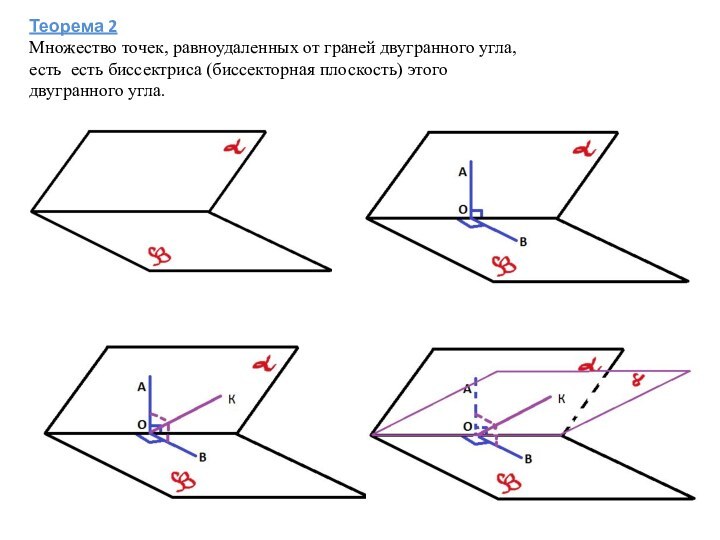
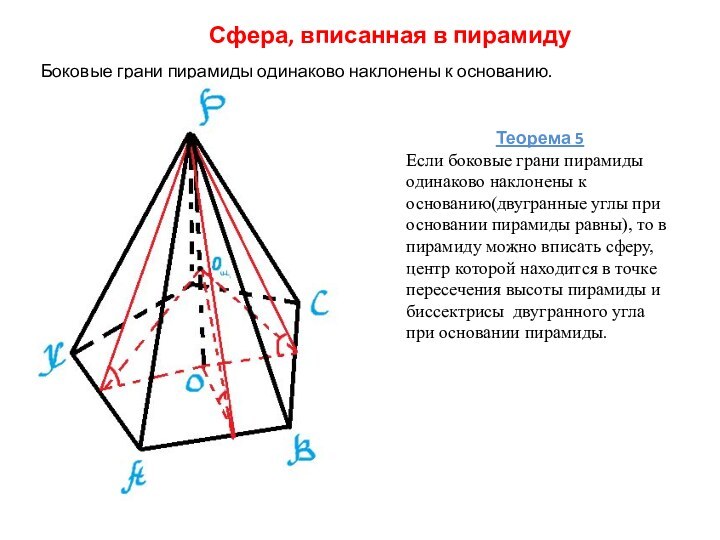
Сфера, вписанная в многогранникОпределение Многогранник называется описанным около сферы(а сфера вписанной в многогранник), если все грани многогранника касаются этой сферы. Следствие Центр вписанной сферы есть точка, равноудаленная от всех граней многогранника.
Слайд 2
Сфера, вписанная в многогранник
Определение
Многогранник называется описанным около
Слайд 3
Подготовительные задачи
1. Где расположено множество точек пространства ,
равноудаленных от двух плоскостей?
Теорема 1
Множество точек, равноудаленных от
двух параллельных плоскостей ,есть плоскость, параллельная данным плоскостям и проходящая через середину общего перпендикуляра этих плоскостей. Дано:
α || β;
γ|| α; γ|| β;
AC=CD; AB |α; AB| β
Слайд 4
Теорема 2
Множество точек, равноудаленных от граней двугранного
угла, есть есть биссектриса (биссекторная плоскость) этого двугранного угла.
Слайд 5
Теорема 3
Множество точек, равноудаленных от граней трехгранного угла,
есть биссектриса этого трехгранного угла.
Биссектрисой трехгранного угла называется луч
с началом в вершине данного трехгранного угла, который образует равные углы с гранями этого трехгранного угла.
Слайд 6
Сфера, вписанная в призму
Теорема 4
В призму можно
вписать сферу тогда и только тогда, когда в перпендикулярное
сечение этой призмы можно вписать окружность, и высота призмы равна диаметру этой окружности (диаметру вписанной сферы).Слайд 7 2. Расстояние между боковыми ребрами треугольной призмы 13,14,15.В
призму вписан шар. Боковое ребро составляет с плоскостью основания
угол α . Найти объем призмы и объем шара.Решение.
(А2В2С2)-перпендикулярное сечение.
Vш.= ⁴⁄₃ПR ш.3
S=⅟₂Prокр
R ш.=rвпис.окр.= S А2В2С2 /p
p =21;
S=√p(p-a) (p-b) (p-c);
S А2В2С2=84;
R ш.=84/21=4;
Vш.= ⁴⁄₃ПR ш.3; Vш.= 256П/3;
2) V пр.=S перп.сеч.*АА1 ;
АА1 =А1О/sin α=8/ sin α;
V пр.=84*8/ sin α =672/ sin α.
Ответ: 256П/3; 672/ sin α.
Слайд 8
Сфера, вписанная в пирамиду
Боковые грани пирамиды одинаково наклонены
к основанию.
Теорема 5
Если боковые грани пирамиды одинаково наклонены к
основанию(двугранные углы при основании пирамиды равны), то в пирамиду можно вписать сферу, центр которой находится в точке пересечения высоты пирамиды и биссектрисы двугранного угла при основании пирамиды.Слайд 9 3.Основание пирамиды- треугольник со сторонами 9,10 и 17.Все
боковые грани наклонены под углом 45о к основанию пирамиды
.Найти радиус вписанного шара.Решение.
1)OK= rвпис.окр. =S/p;
S=p* rвпис.окр . ;p=18;
S=√p(p-a) (p-b) (p-c);
S ∆АВС=36;OK=2.
2) ∆POK: KOш.-биссектриса, т.о.
ООш./Ош.p=OK/PK=cos 45о ;
ООш./Ош.p=1/ √2;
√ 2 Rш.=2-Rш.;
Rш.=2/(1+ √ 2)=2(√ 2-1).
Ответ: 2(√ 2-1).
Слайд 10
Теорема 6
В любой тетраэд можно вписать сферу.
Теорема 7
Если
в многогранник, объем которого равен V,а площадь поверхности равна
S,вписан шар радиуса R,то имеет место соотношение: V=⅓S*R
3.Основание пирамиды- треугольник АВС,В котором АВ|ВС,АВ=4,ВС=3.Боковое ребро РА перпендикулярно плоскости основания пирамиды и равно 3.Найдите объем шара, вписанного в пирамиду.
Решение.
1)Vпир.=⅓S ∆ ABC*AP;
Vпир.=⅓*⅟₂*3*4*3=6.
2)PB|BC(по теореме о трех перпендикулярах);АС=PB=5.
3) S ∆PАВ=S ∆АВС= ⅟₂*4*3=6.
S ∆PВC= S ∆PАC=⅟₂*3*5=7,5.
Sполн.=2*6+2*7,5=12+15=27.
4)Rш.=3 Vпир./S;
Rш.=3*6/27=⅔;
Vш.=⁴⁄₃ПR 3=32П/81.
Ответ: 32П/81.
Слайд 11 4. Шар вписан в прямую призму, основание которой-
равнобедренная трапеция с основаниями 2 и 8.Найдите объем шара
и объем призмы.Решение.
1)Rш.= rвпис.окр . ;Hпр.=D впис.окр.=CK.
2)DC+AB=AD+CB;
2BC=2+8; BC=5.
3)BC=⅟₂(AB-DC); BK= ⅟₂(8-2)=3;
4) ∆BCK:CK=4; Rш.=2.
5)Vпр.=Sосн.*Нпр.;
Vпр.=80;
Vш.= ⁴⁄₃ПR 3 ;
Vш.= ⁴⁄₃П2 3 =32П/3.
Ответ: 32П/3.
