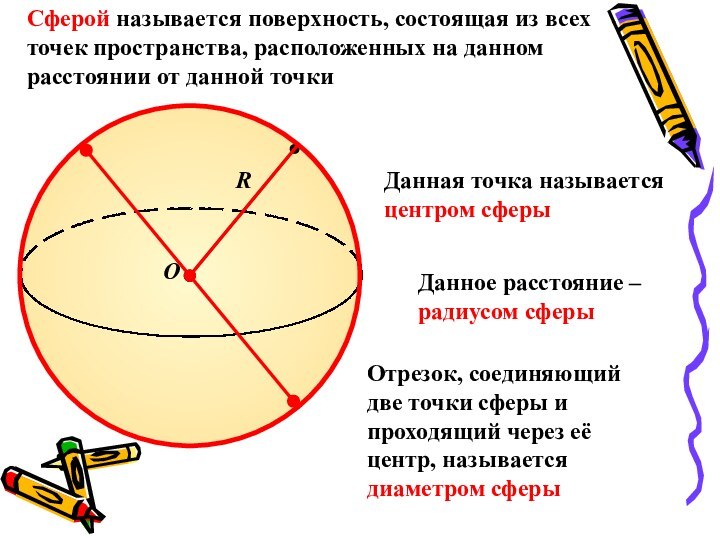
расположенных на данном расстоянии от данной точки
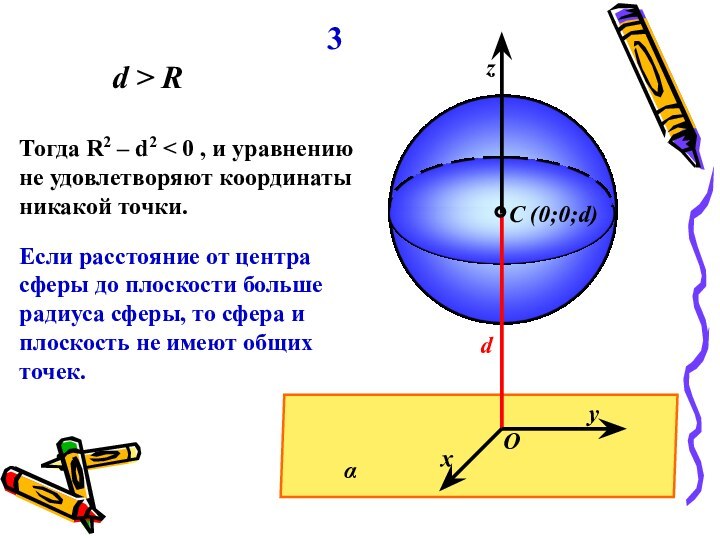
Данная точка называется
центром сферыДанное расстояние – радиусом сферы
Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы