- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
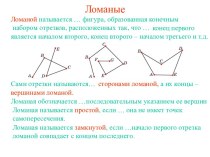
Презентация на тему по геометрии Лист Мебиуса
Содержание
- 2. Август Фердинанд Мёбиус 1790-1868 Немецкий геометр родился
- 3. Опыт №1 (Лента Мёбиуса)Итог: получилось кольцо, вдвое
- 4. Опыт №2 (Разрезание на треть от края)Итог:
- 5. Опыт №3 (Разрезаем на одну четвертую от
- 6. Опыт №4 (Разрезаем ленту с двумя перекрутами.)Итог:
- 7. Опыт №5 (Разрезаем ленту с двумя перекрутами
- 8. Опыт №6 (замкнутая цепочка)Возьмем полоску, перегнутую по
- 9. Лист Мебиуса в скульптуре и архитектуре.г. Минск.
- 10. Это украшение в виде ленты Мебиуса выполнено
- 11. Лист Мёбиуса: грандиозная библиотека в Казахстане
- 12. Изгибы музея образуют лист Мёбиуса,таким образом внутреннее
- 15. Лист Мёбиуса в искусстве. «Узел без конца» Макс Билл«Непрерывность»
- 16. Лиза Рей «Корабль дураков в бесконечность».Лист Мёбиуса в искусстве.
- 17. Известный голландский художник М. Эшер (1898-1971)
- 18. Картинная галерея.
- 19. Печерский Е.И.
- 20. Ювелирные украшения
- 21. Лист Мебиуса в технике Подшипник в виде ленты Мебиусадля увеличения срока работы.Прокатный станМагнитофонная лентаРемень передачи
- 22. Международный символ переработки.
- 23. Занимательные игры
- 24. Топологические фокусы Как завязать на шарфе узел, не выпуская из рукего концов?
- 25. Топологические фокусы Как можно вывернуть наизнанку жилет,не снимая его?
- 26. Скачать презентацию
- 27. Похожие презентации
Август Фердинанд Мёбиус 1790-1868 Немецкий геометр родился в городе Шульпфорте. Профессор Лейпцигского университета с 1816 года. Установил существование односторонних поверхностей (1858г.), одна из которых - лист Мёбиуса.


























Слайд 2
Август Фердинанд Мёбиус 1790-1868
Немецкий геометр родился в
городе Шульпфорте.
Установил существование односторонних поверхностей (1858г.), одна из которых - лист Мёбиуса.
Слайд 3
Опыт №1
(Лента Мёбиуса)
Итог: получилось кольцо, вдвое уже, но
зато вдвое длиннее.
К тому
же, перекручено оно не один раз, а два.
Слайд 4
Опыт №2
(Разрезание на треть от края)
Итог: получаются две
ленты, одна - короткая лента Мебиуса,
другая - длинная лента с двумя перекрутами.
Слайд 5
Опыт №3
(Разрезаем на одну четвертую от края.)
Итог: получается
2 кольца вдвое длиннее первоначальной
ленты и вдвое перекрученные, сцепленные междусобой.
Слайд 6
Опыт №4
(Разрезаем ленту с двумя перекрутами.)
Итог: получили два
кольца с двумя перекрутами,
сцепленные
друг с другом.Слайд 7 Опыт №5 (Разрезаем ленту с двумя перекрутами на одну
треть от края. )
Итог: получаем один лист Мебиуса и
два кольца с двумяперекрутами.
Слайд 8
Опыт №6
(замкнутая цепочка)
Возьмем полоску, перегнутую по длине один
раз.
Перекрутим ее на полный оборот и склеим концы, накладывая
«домиком» один конец на другой.Теперь разрежем двойной слой склеенной ленты по ее средней линии.
Получатся три кольца, сцепленные попарно.
Слайд 9
Лист Мебиуса в скульптуре и архитектуре.
г. Минск. Скверик
около Центральной Научной
библиотеки имени Якуба Коласа.Слайд 10 Это украшение в виде ленты Мебиуса выполнено в
Риге в 2001 году.
Лист Мебиуса в скульптуре и архитектуре.
г.
Москва
Слайд 12
Изгибы музея образуют лист Мёбиуса,
таким образом внутреннее пространство
переходит во внешнее и обратно; подобным образом стены переходят
в крышу,а крыша трансформируется
обратно в стены.