Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему по геометрии на тему Метод следов

Содержание

Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений.Комбинированный метод.
Построение сечений: метод следовАстрахань – 2012 г. Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений.Комбинированный метод. Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани Задача 1.Дана призма ABCDA1B1C1D1.Построить сечение призмы плоскостью, проходящей через точки P, Q, R.PQR Задача 1.Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ. Задача 1.Прямая PQ, которая принадлежит сечению, пересекается с прямой АВ в точке S1. 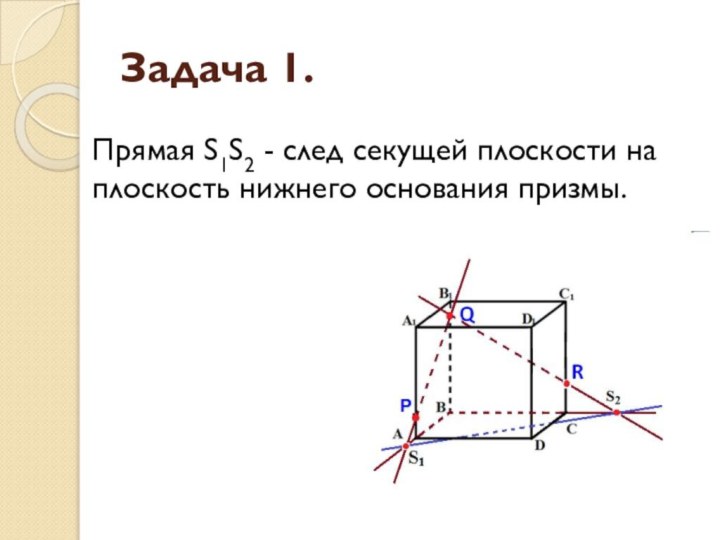Задача 1.Аналогично получаем точку S2 пересечением прямых QR и BC. Задача 1.Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы. 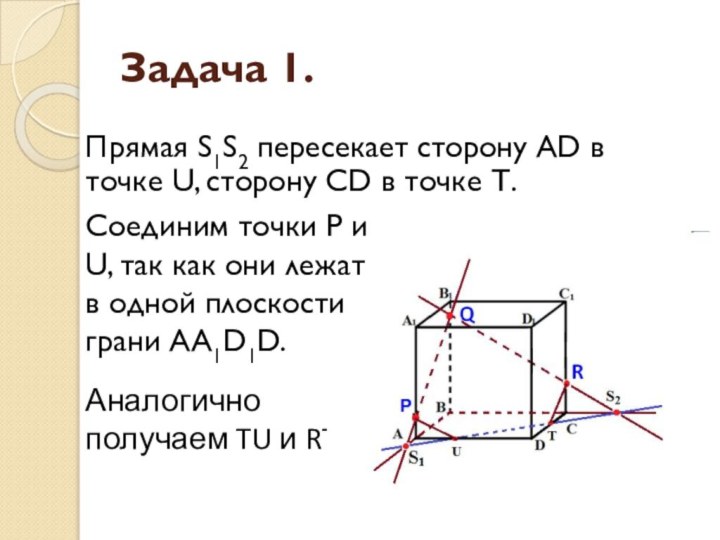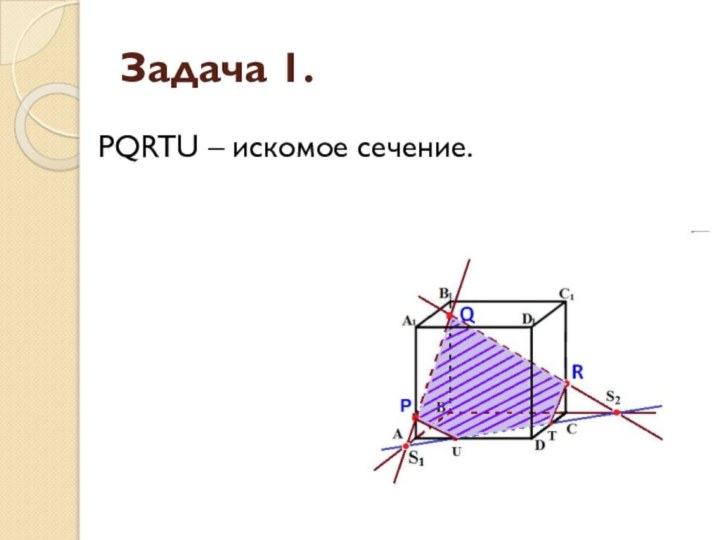Задача 1.Прямая S1S2 пересекает сторону AD в точке U, сторону CD в Задача 1.PQRTU – искомое сечение. 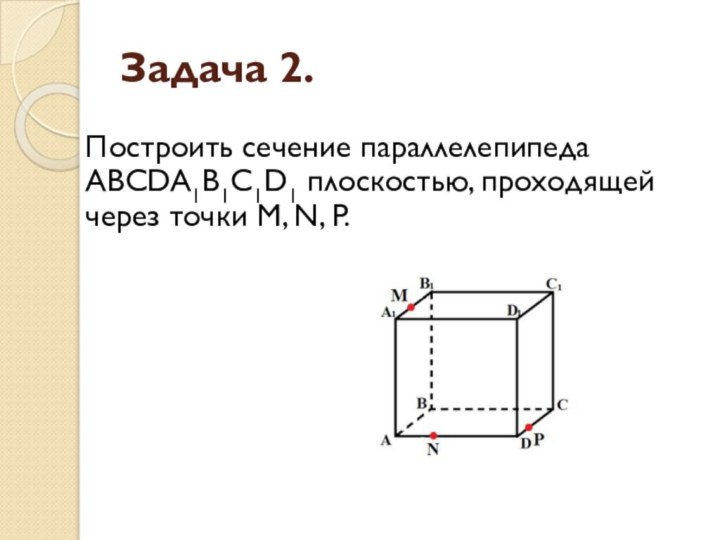Задача 2.Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P. 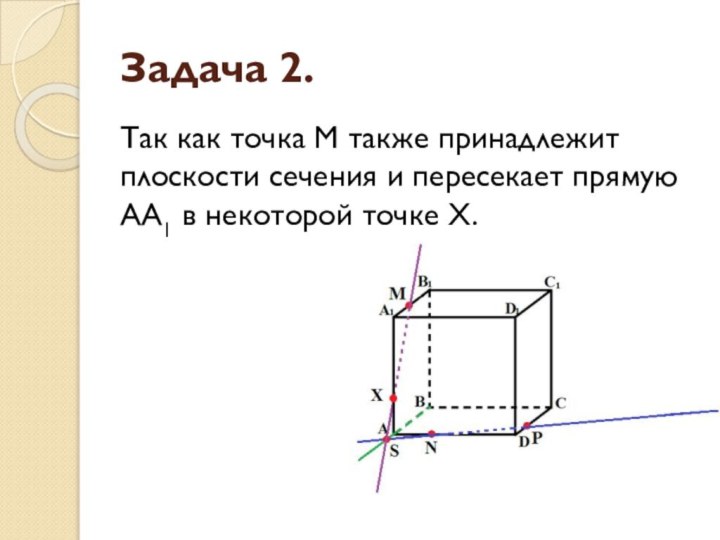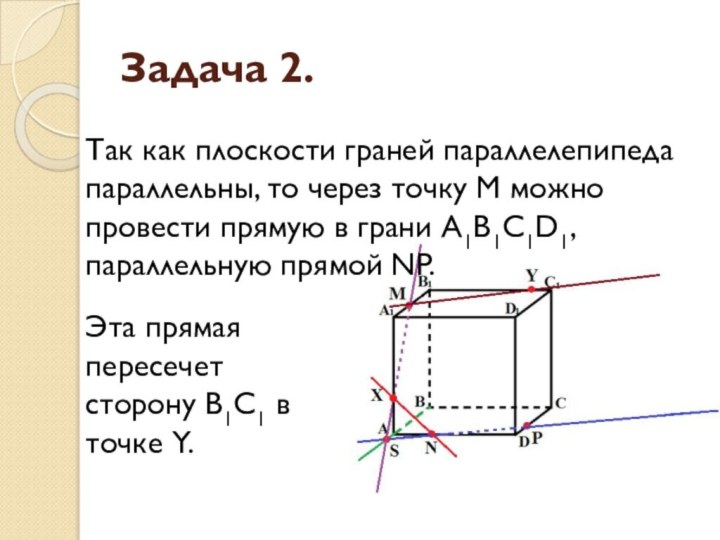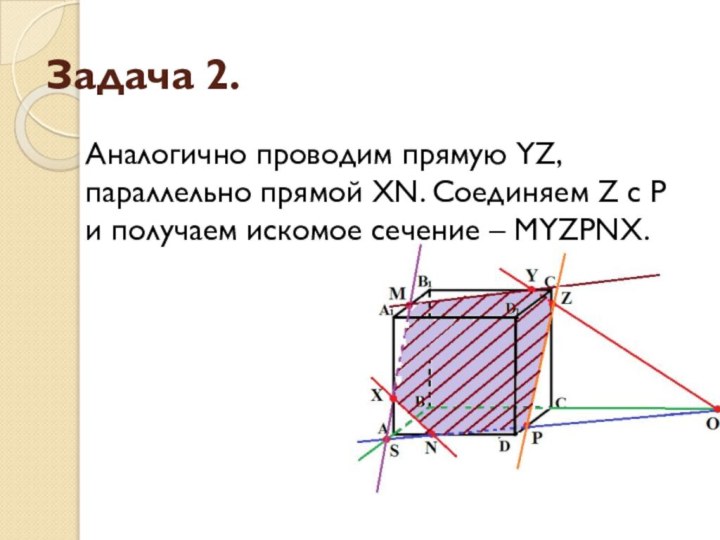Задача 2.Точки N и P лежат в плоскости сечения и в плоскости Задача 2.Продолжим прямую, на которой лежит сторона AB параллелепипеда.Прямые AB и NP Задача 2.Так как точка M также принадлежит плоскости сечения и пересекает прямую Задача 2.Точки X и N лежат в одной плоскости грани АА1D1D, соединим Задача 2.Эта прямая пересечет сторону В1С1 в точке Y.Так как плоскости граней Задача 2.Аналогично проводим прямую YZ, параллельно прямой XN. 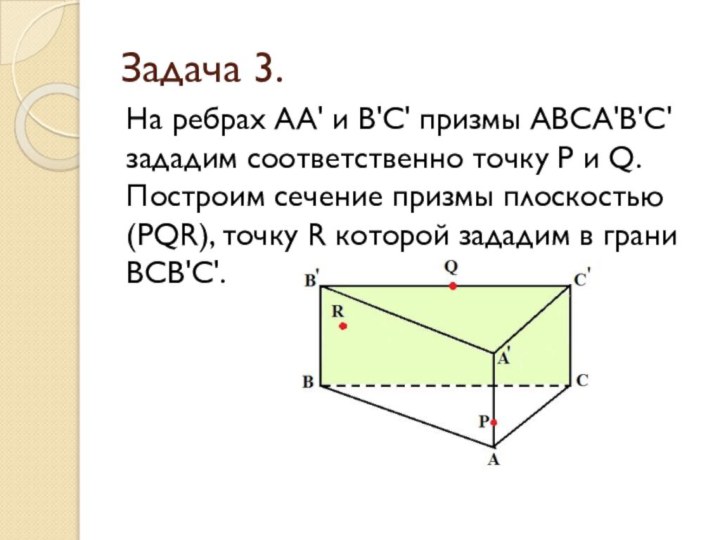Соединяем Z с P Задача 3.На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку P Задача 3.Так как точки Q и R лежат в плоскости (ВСС'), то Задача 3.Находим точки В'' и С'' , в которых прямая QR пересекает Задача 3.Так как точки В'' и Р лежат в плоскости (АВВ'), то Задача 3.Так как точки Р и С лежат в плоскости (АСС'), то Задача 3.Находим точку V, в которой прямая РС'' пересекает ребро А'С'. 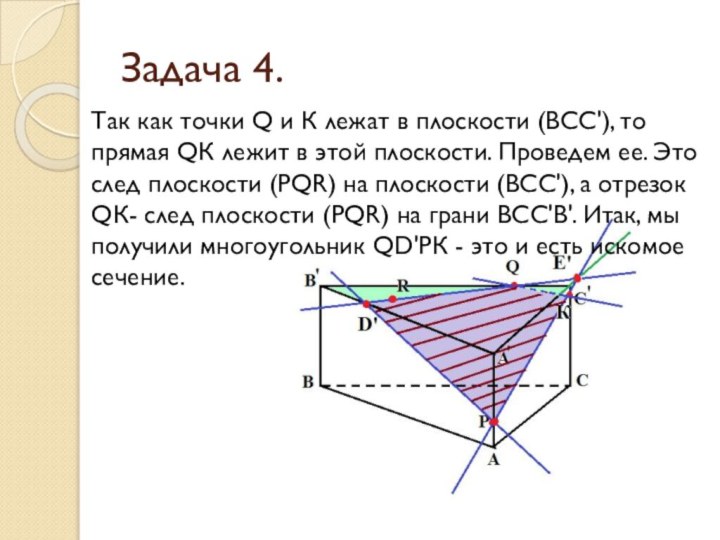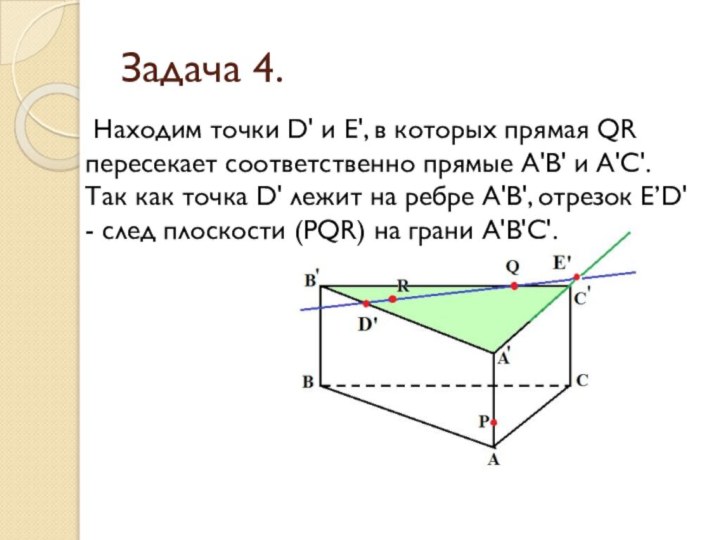Это Задача 3.Так как точки Q и V лежат в плоскости (А'В'С'), то Задача 4.На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку P Задача 4.Так как точки Q и R лежат в плоскости (А'В'С'), то Задача 4. 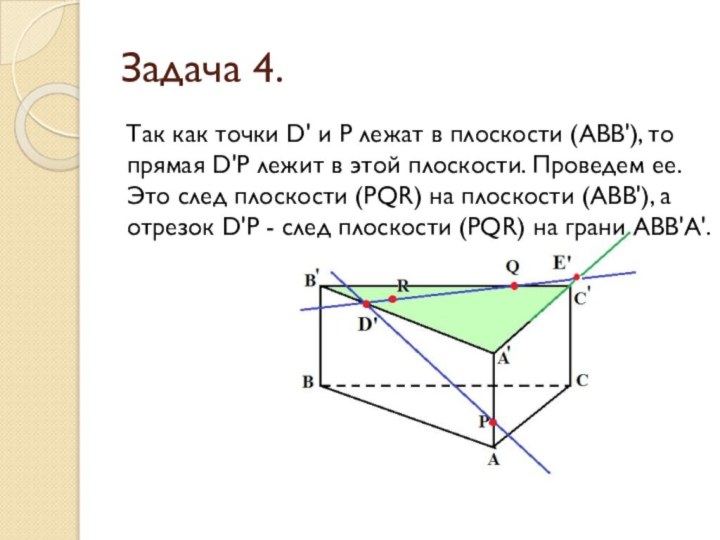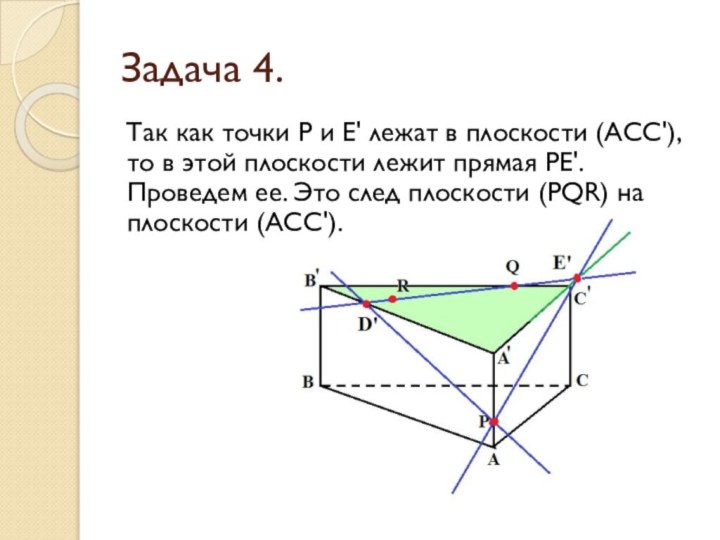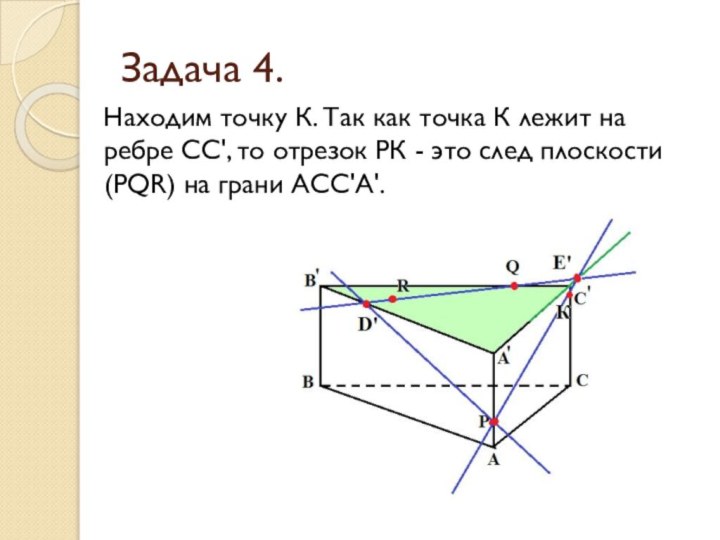Находим точки D' и Е', в которых прямая QR пересекает Задача 4.Так как точки D' и P лежат в плоскости (АВВ'), то Задача 4.Так как точки Р и Е' лежат в плоскости (АСС'), то Задача 4.Находим точку К. Так как точка К лежит на ребре СС', Задача 4.Так как точки Q и К лежат в плоскости (ВСС'), то Спасибо за внимание!
Слайды презентации

Слайд 2 Существует три основных метода построения сечений многогранников:

Метод

Существует три основных метода построения сечений многогранников: Метод следов. Метод вспомогательных сечений.Комбинированный метод.

следов.
Метод вспомогательных сечений.
Комбинированный метод.

Слайд 3 Метод следов заключается в построении следов секущей плоскости

Метод следов заключается в построении следов секущей плоскости на плоскость каждой

на плоскость каждой грани многогранника.
Построение сечения многогранника методом

следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.

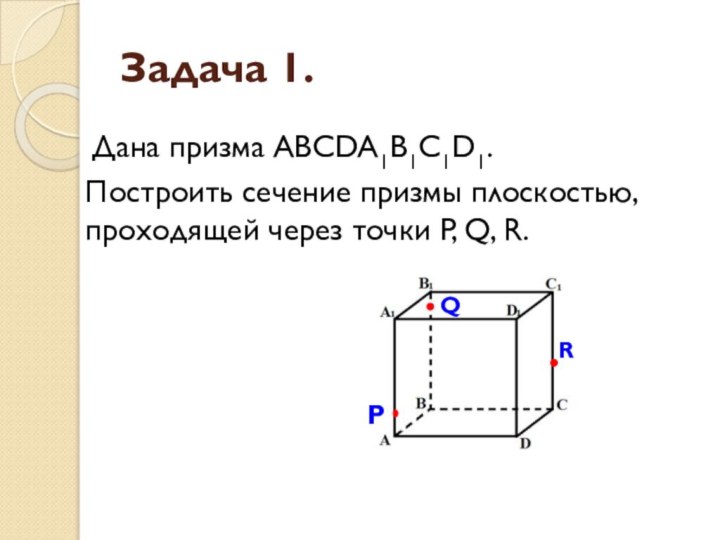
Слайд 4 Задача 1.
Дана призма ABCDA1B1C1D1.
Построить сечение призмы плоскостью, проходящей

Задача 1.Дана призма ABCDA1B1C1D1.Построить сечение призмы плоскостью, проходящей через точки P, Q, R.PQR

через точки P, Q, R.

P
Q
R

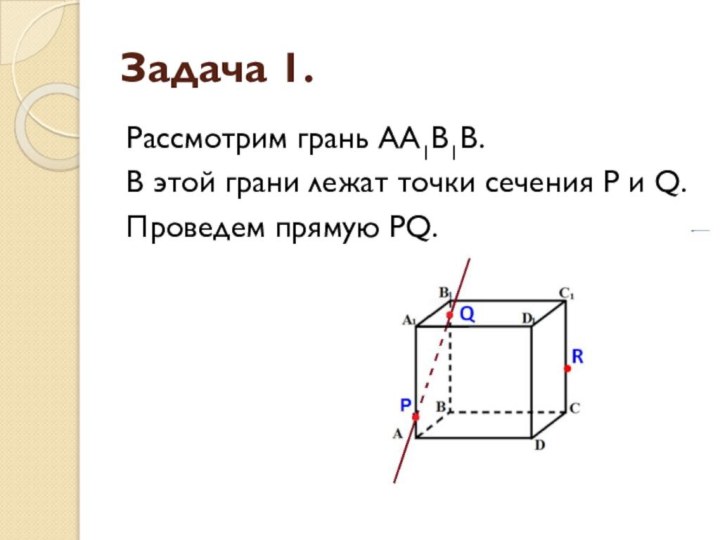
Слайд 5 Задача 1.
Рассмотрим грань АА1В1В.
В этой грани лежат

Задача 1.Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.

точки сечения P и Q.
Проведем прямую PQ.

Слайд 6 Задача 1.
Прямая PQ, которая принадлежит сечению, пересекается с

Задача 1.Прямая PQ, которая принадлежит сечению, пересекается с прямой АВ в точке S1.

прямой АВ в точке S1.

Слайд 7 Задача 1.
Аналогично получаем точку S2 пересечением прямых QR

Задача 1.Аналогично получаем точку S2 пересечением прямых QR и BC.

и BC.

Слайд 8 Задача 1.
Прямая S1S2 - след секущей плоскости на

Задача 1.Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы.

плоскость нижнего основания призмы.

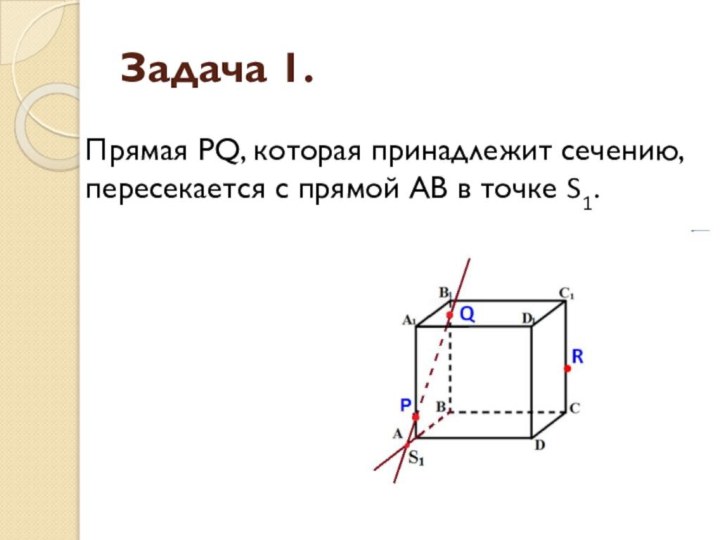
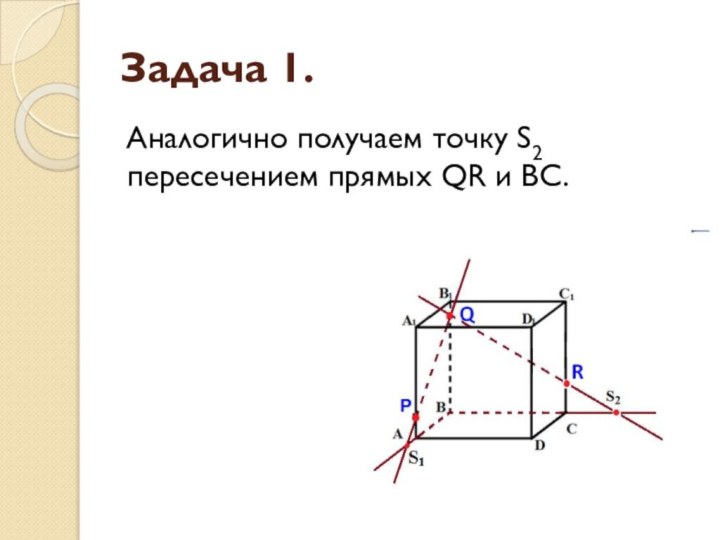
Слайд 9 Задача 1.
Прямая S1S2 пересекает сторону AD в точке

Задача 1.Прямая S1S2 пересекает сторону AD в точке U, сторону CD

U, сторону CD в точке Т.
Аналогично получаем TU

и RT.

Соединим точки P и U, так как они лежат в одной плоскости
грани АА1D1D.

Слайд 10 Задача 1.
PQRTU – искомое сечение.

Задача 1.PQRTU – искомое сечение.

Слайд 11 Задача 2.
Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через

Задача 2.Построить сечение параллелепипеда ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P.

точки M, N, P.

Слайд 12 Задача 2.
Точки N и P лежат в плоскости

Задача 2.Точки N и P лежат в плоскости сечения и в

сечения и в плоскости нижнего основания параллелепипеда. Построим прямую,

проходящую через эти точки.

Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.

Слайд 13 Задача 2.
Продолжим прямую, на которой лежит сторона AB

Задача 2.Продолжим прямую, на которой лежит сторона AB параллелепипеда.Прямые AB и

параллелепипеда.
Прямые AB и NP пересекутся в некоторой точке S.
Эта

точка принадлежит плоскости сечения.

Слайд 14 Задача 2.
Так как точка M также принадлежит плоскости

Задача 2.Так как точка M также принадлежит плоскости сечения и пересекает

сечения и пересекает прямую АА1 в некоторой точке Х.

Слайд 15 Задача 2.
Точки X и N лежат в одной

Задача 2.Точки X и N лежат в одной плоскости грани АА1D1D,

плоскости грани АА1D1D, соединим их и получим прямую XN.

Слайд 16 Задача 2.
Эта прямая пересечет сторону В1С1 в точке

Задача 2.Эта прямая пересечет сторону В1С1 в точке Y.Так как плоскости

Y.
Так как плоскости граней параллелепипеда параллельны, то через точку

M можно провести прямую в грани A1B1C1D1, параллельную прямой NP.

Слайд 17 Задача 2.

Аналогично проводим прямую YZ, параллельно прямой XN.

Задача 2.Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с

Соединяем Z с P и получаем искомое сечение –

MYZPNX.

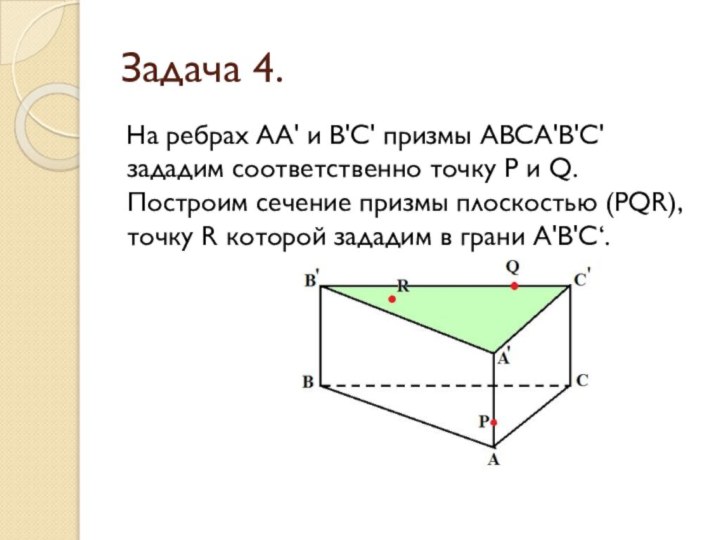
Слайд 18 Задача 3.
На ребрах АА' и В'С' призмы АВСА'В'С'

Задача 3.На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку

зададим соответственно точку P и Q. Построим сечение призмы

плоскостью (PQR), точку R которой зададим в грани ВСВ'С'.

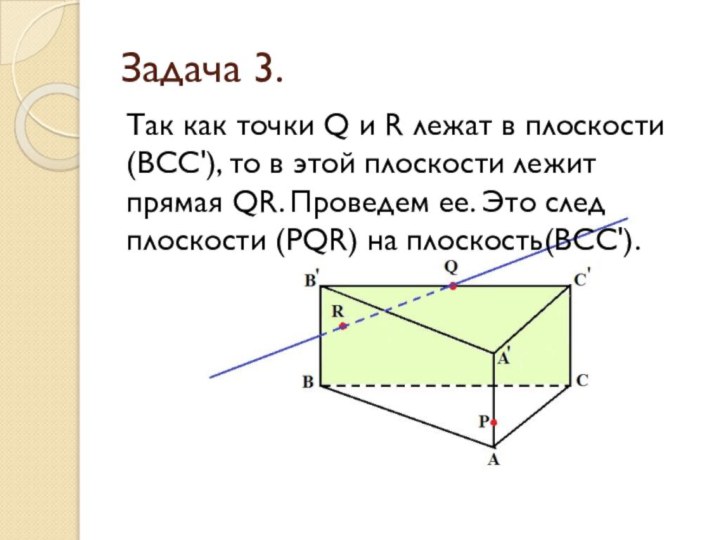
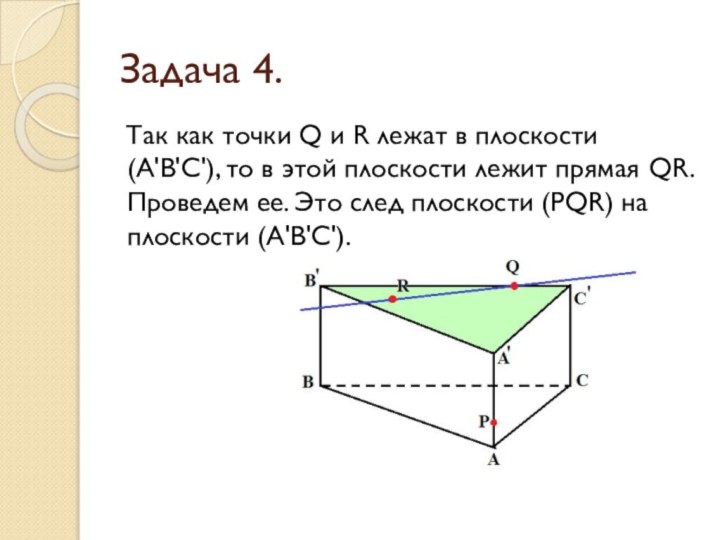
Слайд 19 Задача 3.
Так как точки Q и R лежат

Задача 3.Так как точки Q и R лежат в плоскости (ВСС'),

в плоскости (ВСС'), то в этой плоскости лежит прямая

QR. Проведем ее. Это след плоскости (PQR) на плоскость(ВСС').

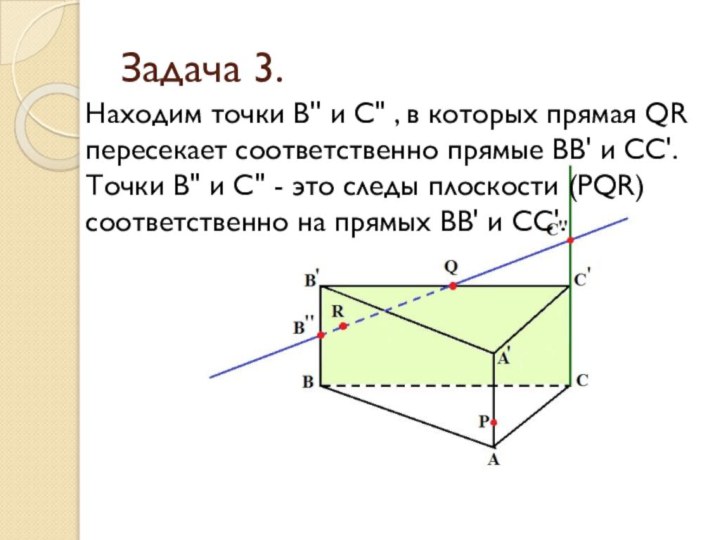
Слайд 20 Задача 3.
Находим точки В'' и С'' , в

Задача 3.Находим точки В'' и С'' , в которых прямая QR

которых прямая QR пересекает соответственно прямые ВВ' и СС'.

Точки В'' и С'' - это следы плоскости (PQR) соответственно на прямых ВВ' и СС'.

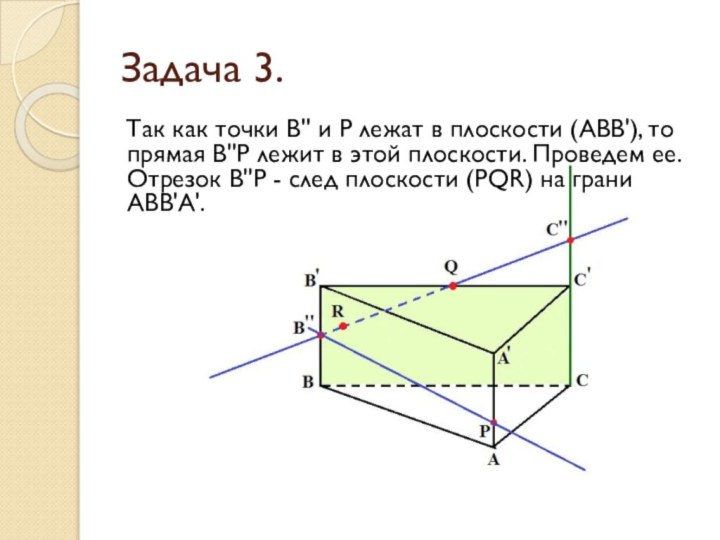
Слайд 21 Задача 3.
Так как точки В'' и Р лежат

Задача 3.Так как точки В'' и Р лежат в плоскости (АВВ'),

в плоскости (АВВ'), то прямая В''Р лежит в этой

плоскости. Проведем ее. Отрезок В''Р - след плоскости (PQR) на грани АВВ'А'.

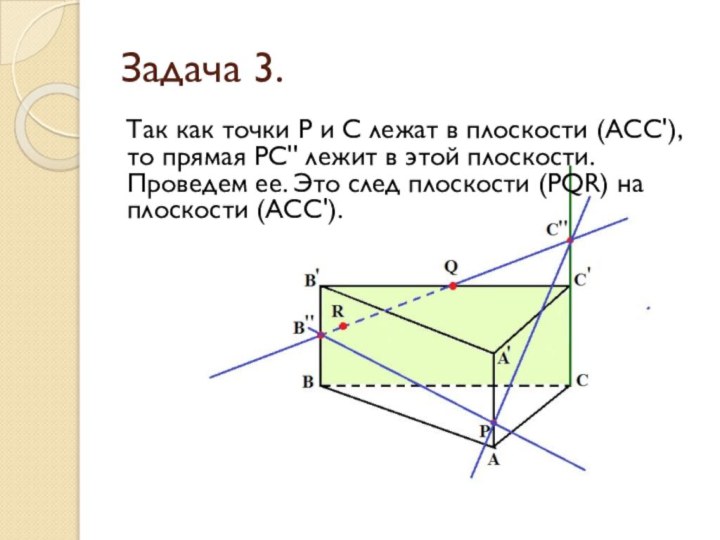
Слайд 22 Задача 3.
Так как точки Р и С лежат

Задача 3.Так как точки Р и С лежат в плоскости (АСС'),

в плоскости (АСС'), то прямая РС'' лежит в этой

плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').

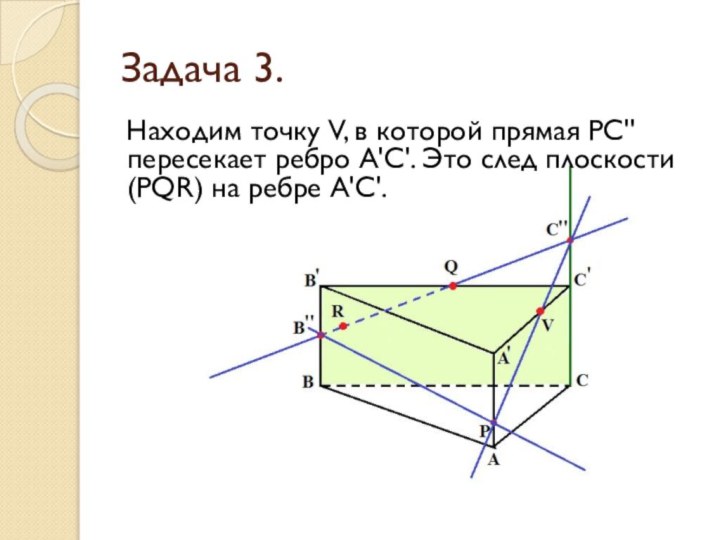
Слайд 23 Задача 3.
Находим точку V, в которой прямая РС''

Задача 3.Находим точку V, в которой прямая РС'' пересекает ребро А'С'.

пересекает ребро А'С'. Это след плоскости (PQR) на ребре

А'С'.

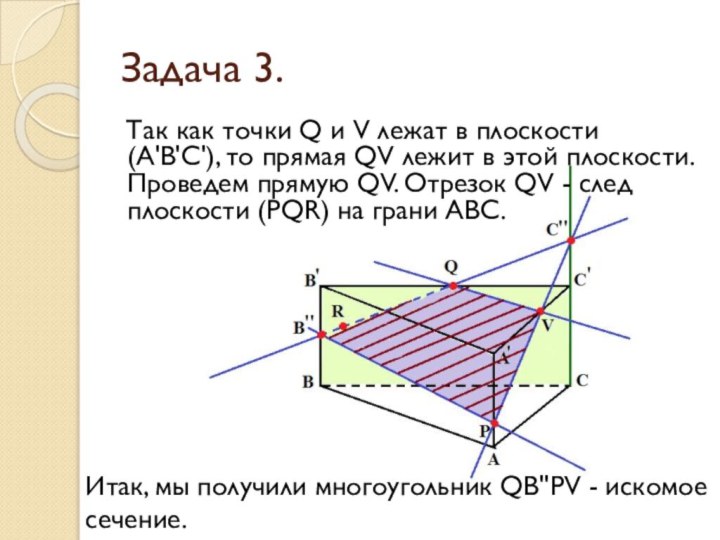
Слайд 24 Задача 3.
Так как точки Q и V лежат

Задача 3.Так как точки Q и V лежат в плоскости (А'В'С'),

в плоскости (А'В'С'), то прямая QV лежит в этой

плоскости. Проведем прямую QV. Отрезок QV - след плоскости (PQR) на грани АВС.

Итак, мы получили многоугольник QB''PV - искомое сечение.

Слайд 25 Задача 4.
На ребрах АА' и В'С' призмы АВСА'В'С'

Задача 4.На ребрах АА' и В'С' призмы АВСА'В'С' зададим соответственно точку

зададим соответственно точку P и Q. Построим сечение призмы

плоскостью (PQR), точку R которой зададим в грани А'В'С‘.

Слайд 26 Задача 4.
Так как точки Q и R лежат

Задача 4.Так как точки Q и R лежат в плоскости (А'В'С'),

в плоскости (А'В'С'), то в этой плоскости лежит прямая

QR. Проведем ее. Это след плоскости (PQR) на плоскости (А'В'С').

Слайд 27 Задача 4.
Находим точки D' и Е', в

Задача 4. Находим точки D' и Е', в которых прямая QR

которых прямая QR пересекает соответственно прямые А'В' и А'С'.

Так как точка D' лежит на ребре А'В', отрезок Е’D' - след плоскости (PQR) на грани А'В'С'.

Слайд 28 Задача 4.
Так как точки D' и P лежат

Задача 4.Так как точки D' и P лежат в плоскости (АВВ'),

в плоскости (АВВ'), то прямая D'P лежит в этой

плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (АВВ'), а отрезок D'P - след плоскости (PQR) на грани АВВ'А'.

Слайд 29 Задача 4.
Так как точки Р и Е' лежат

Задача 4.Так как точки Р и Е' лежат в плоскости (АСС'),

в плоскости (АСС'), то в этой плоскости лежит прямая

РЕ'. Проведем ее. Это след плоскости (PQR) на плоскости (АСС').


Слайд 30 Задача 4.
Находим точку К. Так как точка К

Задача 4.Находим точку К. Так как точка К лежит на ребре

лежит на ребре СС', то отрезок РК - это

след плоскости (PQR) на грани АСС'А'.

Слайд 31 Задача 4.
Так как точки Q и К лежат

Задача 4.Так как точки Q и К лежат в плоскости (ВСС'),

в плоскости (ВСС'), то прямая QК лежит в этой

плоскости. Проведем ее. Это след плоскости (PQR) на плоскости (ВСС'), а отрезок QК- след плоскости (PQR) на грани ВСС'В'. Итак, мы получили многоугольник QD'РК - это и есть искомое сечение.
  • Имя файла: prezentatsiya-po-geometrii-na-temu-metod-sledov.pptx
  • Количество просмотров: 186
  • Количество скачиваний: 0
- Предыдущая Презентация по математике Задачи на готовых чертежах (8 класс)
Следующая - Презентация к уроку литературного чтения на тему: К.И. Чуковский Телефон

Похожие презентации

Квадрат Пирсона Квадрат Пирсона 149
Измерение углов 5 класс Измерение углов 5 класс 369
Соединения деталей Соединения деталей 146
Презентация по геометрии Вписанные углы (8 класс) Презентация по геометрии Вписанные углы (8 класс) 155
Пирамида. Сечения пирамиды Пирамида. Сечения пирамиды 169
Решение задач. Прямоугольник, ромб, квадрат и их свойства Решение задач. Прямоугольник, ромб, квадрат и их свойства 275
Путешествие в страну Геометрия Путешествие в страну Геометрия 174
Презентация по теме: Цилиндр Презентация по теме: Цилиндр 168
Презентация по геометрии Тест по теме Параллельные прямые Презентация по геометрии Тест по теме Параллельные прямые 175
Презентация по геометрии в 7 классе Презентация по геометрии в 7 классе 167
Скалярное произведение векторов Скалярное произведение векторов 206
Тетраэдр и Параллелепипед Тетраэдр и Параллелепипед 144
Презентация к уроку геометрии 8 класс по теме Площади.(Обобщающий урок) Презентация к уроку геометрии 8 класс по теме Площади.(Обобщающий урок) 159
Презентация по математике Свойство биссектрисы угла (8 класс) Презентация по математике Свойство биссектрисы угла (8 класс) 242
Построение треугольника по трем элементам Построение треугольника по трем элементам 176
Геометрия пирамида Геометрия пирамида 163
Презентация по геометрии Теорема Пифагора Презентация по геометрии Теорема Пифагора 164
Kompas Kompas 137
Геометрические формы в разных архитектурных стилях Геометрические формы в разных архитектурных стилях 181
Презентация по геометрии на тему Первый признак равенства треугольников (7 класс) Презентация по геометрии на тему Первый признак равенства треугольников (7 класс) 143
Векторы в пространстве Векторы в пространстве 141
Презентация по матемаике на тему Решение задач на нахождение поверхности цилиндра Презентация по матемаике на тему Решение задач на нахождение поверхности цилиндра 222
Простейшие тригонометрические уравнения Простейшие тригонометрические уравнения 188
Ломаная линия Ломаная линия 165
1 признак равенства треугольников 1 признак равенства треугольников 152
Построение четвёртого пропорционального отрезка Построение четвёртого пропорционального отрезка 200
Параллелепипед Параллелепипед 141
Презентация по математике на тему Многоугольники Презентация по математике на тему Многоугольники 153
Презентация по геометрии на тему Значения синуса, косинуса и тангенса углов 30, 45, 60 градусов (5 класс) Презентация по геометрии на тему Значения синуса, косинуса и тангенса углов 30, 45, 60 градусов (5 класс) 202
Презентация Мәтінді есептерді квадрат теңдеулерді шешуде қолдану Презентация Мәтінді есептерді квадрат теңдеулерді шешуде қолдану 354