Презентация на тему Окружность и её элементы ( 8 класс)

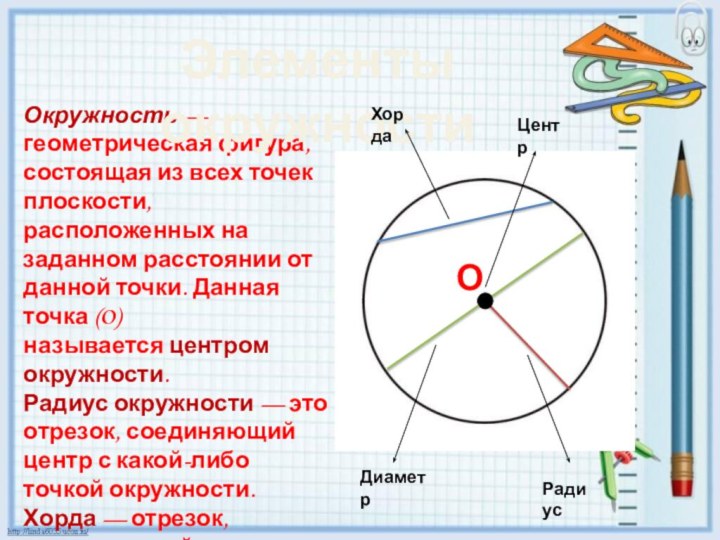
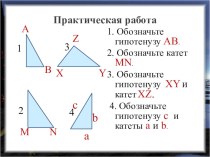
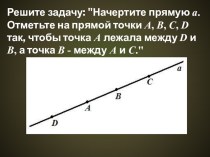
расположенных на заданном расстоянии от данной точки. В Древней

Греции круг и окружность считали венцом совершенства. В каждой своей точке окружность устроена одинаковым образом, что позволяет ей двигаться самой по себе. Это свойство окружности стало толчком к возникновению колеса, так как ось и втулка колеса должны всё время быть в соприкосновении. К сожалению, неизвестен изобретатель колеса. Колесо – это чудо! Что же в нём особенного? Но это только на первый взгляд. Представьте себе на секунду, что вдруг на Земле исчезли все колёса!

История окружности

расположенных на заданном расстоянии от данной точки. Данная точка

(O) называется центром окружности. Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром.

Элементы окружности

О

Хорда

Радиус

Центр

Диаметр

ограниченная дугой и двумя радиусами, соединяющими концы дуги с

центром круга. Дуга, которая ограничивает сектор, называется дугой сектора. Две окружности, имеющие общий центр, называются концентрическими. Прямая, имеющая только одну общую точку с окружностью называется касательной к окружности. Прямая, проходящая через две различных точки окружности, называется секущей.

Элементы окружности

Центральный угол — угол с вершиной в центре окружности. Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Касательная

Секущая

Сектор

Дуга

Концентрические окружности

Центральный угол

– дважды, "метрио” – измеряю) КРУГ. Общеславянское слово, имеющее соответствия

в германских языках: в древнегерманском "кригер" — "кольцо", "круг", в греческом - "колесо", "круг"). ОКРУЖНОСТЬ. В переводе с греческого это слово означает "периферия". РАДИУС. Слово происходит от латинского "радиус" — "луч", "спица в ко­лесе". Термин становится общепринятым лишь в конце XVII в. ЦЕНТР. Произошло от латинского слова ''центрум", которое, в свою оче­редь, произошло от древнегреческого "кентрон", означавшего "колющее ору­дие", "острие ножки циркуля". ХОРДА. Происходит от греческого слова «хорде» — «кишка», «струна» (в древней Греции струны выделывались из воловьих кишок)

ИСРИЯ ПРОИСХОЖДЕНИЯ ТЕРМИНОВ

точек; иметь с окружностью одну общую точку (касательная); иметь

с ней две общие точки (секущая).
2)Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
3)Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
4)Точка касания двух окружностей лежит на отрезке, соединяющем их центры.                   5)Длину окружности с радиусом   можно вычислить по формуле 
6)Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°. 7)Два вписанных угла, опирающиеся на одну и ту же дугу, равны.

окружности равен 90°.
9)Угол между двумя секущими, проведёнными из точки,

лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.
10)Угол между пересекающимися хордами равен полусумме мер дуги лежащей в угле и дуги напротив нее.
11)Угол между касательной и хордой равен половине градусной меры дуги, стягиваемой хордой.
12)Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
13)При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.

Свойства окружности

точек пересечения окружности и секущей, проходящей через выбранную точку,

не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности. 15)Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.
16)Окружность является простой плоской кривой второго порядка.
17)Окружность является коническим сечением и частным случаем эллипса. 18)Длина дуги окружности радиуса , образованной центральным углом , измеренным в радианах, можно вычислить по формуле 

Свойства окружности

началась в Древнем Египте. Площадь круга диаметром d египетские математики определяли

как (d-d/9)2 (эта запись дана здесь в современных символах). Из приведенного выражения можно заключить, что в то время число pосчитали равным дроби (16/9)2, или 256/81, т.е. p = 3,160... В священной книге джайнизма (одной из древнейших религий, существовавших в Индии и возникшей в VI в. до н.э.) имеется указание, из которого следует, что число p в то время принимали равным  , что даёт дробь 3,162...  Древние греки Евдокс, Гиппократ и другие измерение окружности сводили к построению отрезка, а измерение круга - к построению равновеликого квадрата. Следует заметить, что на протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом.

История происхождения числа р(пи)