Презентация на тему Следствия

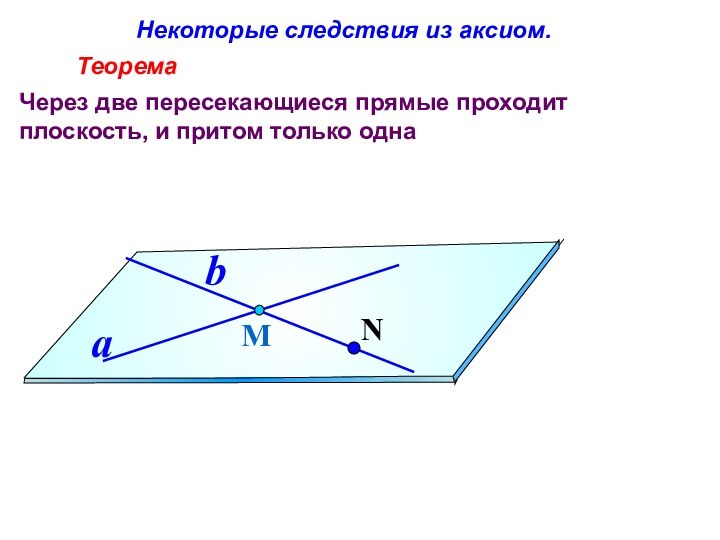
Теорема
Через прямую и не лежащую на ней точку

М

a

Наглядной иллюстрацией следствия из аксиомы является карандаш лежащий

ей точку можно провести плоскость, и притом только одну.

м

А

В

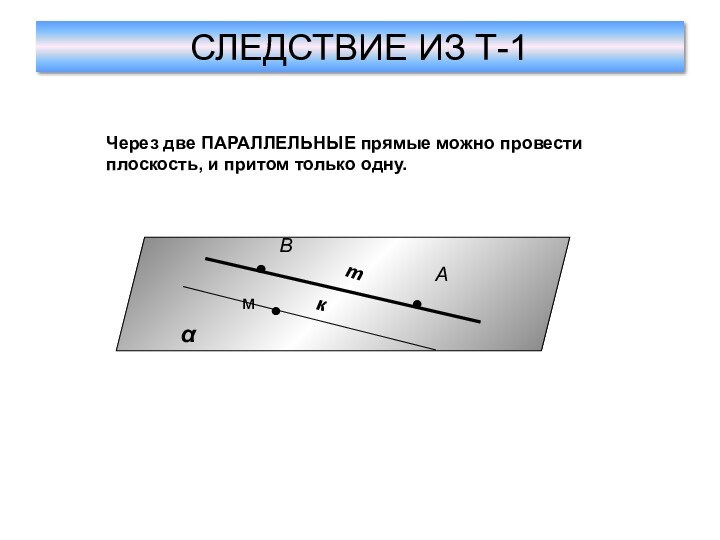
Дано: М∉m

Так как М∉m, то точки А, В и M не принадлежат одной прямой. По А-1 через точки А, В и M проходит только одна плоскость — плоскость (ABM), Обозначим её α. Прямая m имеет с ней две общие точки — точки A и B, следовательно, по аксиоме А-2 эта прямая лежит в плоскости α.. Таким образом, плоскость α проходит через прямую m и точку M и является искомой.
Докажем, что другой плоскости, проходящей через прямую m и точку M, не существует. Предположим, что есть другая плоскость — β, проходящая через прямую m и точку M. Тогда плоскости α и β проходят через точки А, В и M, не принадлежащие одной прямой, а значит, совпадают. Следовательно, плоскость α единственна.
Теорема доказана

Доказательство

Пусть точки A, B ∈ m.

плоскость, и притом только одну.
к

Теорема
Через две пересекающиеся прямые проходит плоскость, и притом

М

a

b

N