- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Ромб
Содержание
- 2. Задача №1Ромб и квадрат имеют одинаковые стороны.
- 3. Задача №2 Найдите площадь ромба, если его
- 4. Задача №3
- 5. Задача №4Диагонали ромба АВСD равны 12 и 16. Найдите
- 6. Задача №5Диагонали ромба ABCD пересекаются в точке O и равны 12
- 7. Задача №6Диагонали ромба ABCD пересекаются в точке O и равны 12
- 8. Задача №7Найдите площадь ромба, если его высота
- 9. Задача №8Площадь ромба равна 6. Одна из
- 10. Задача №9Найдите меньшую диагональ ромба, стороны которого
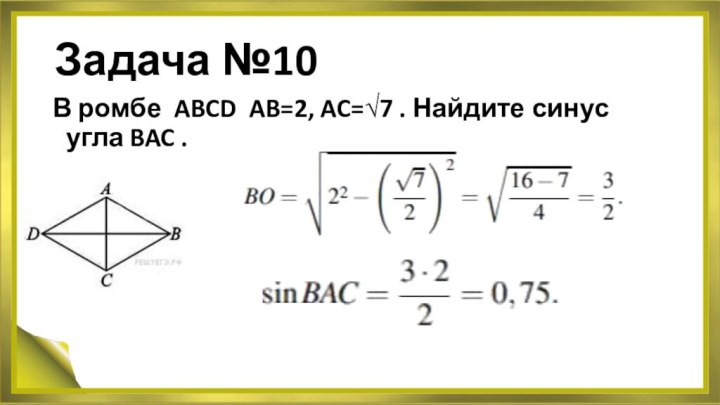
- 11. Задача №10В ромбе ABCD AB=2, AC=√7 . Найдите синус угла BAC .
- 12. Задача №11В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ
- 13. Задача №12
- 14. Скачать презентацию
- 15. Похожие презентации
Задача №1Ромб и квадрат имеют одинаковые стороны. Найдите площадь ромба, если его острый угол равен 30°, а площадь квадрата равна 64.











Слайд 4
Задача №3
Диагонали
ромба АВСD равны 12 и 16. Найдите длину вектора AB .
Диагонали
ромба пересекаются под прямым углом и точкой пересечения делятся пополам. Тогда вектор АВ является гипотенузой в прямоугольном треугольнике. По теореме Пифагора получаем, что
Слайд 5
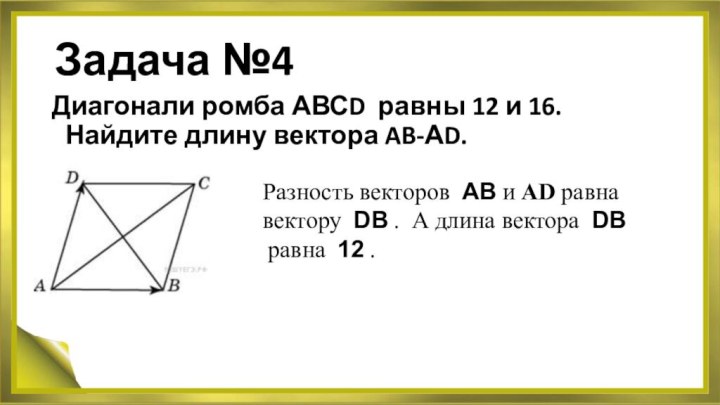
Задача №4
Диагонали ромба АВСD равны 12 и 16. Найдите длину
вектора AB-АD.
Разность векторов АВ и АD равна
вектору DB . А длина вектора
DBравна 12 .
Слайд 6
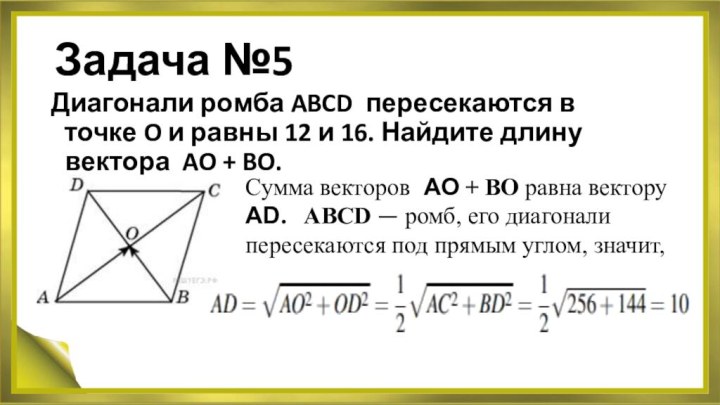
Задача №5
Диагонали ромба ABCD пересекаются в точке O и равны 12 и
16. Найдите длину вектора AO + BO.
Сумма векторов AO + BO равна
векторуAD. ABCD — ромб, его диагонали
пересекаются под прямым углом, значит,
Слайд 7
Задача №6
Диагонали ромба ABCD пересекаются в точке O и равны 12 и
16. Найдите скалярное произведение векторов АО и ВО.
Скалярное произведение
двух векторов равно произведению их длин на косинус угла между ними. Диагонали в ромбе перпендикулярны. Так как косинус прямого угла равен нулю, то и скалярное произведение тоже равно нулю.
Слайд 8
Задача №7
Найдите площадь ромба, если его высота равна
2, а его острый угол равен 30°.
Площадь ромба равна
произведению квадрата его стороны на синус его угла. С другой стороны, площадь ромба равна произведению его основания на высоту, опущенную на это основание. Поэтому, если сторона ромба равна а, то Решаем полученное уравнении и
получаем а=4, поэтому
Слайд 9
Задача №8
Площадь ромба равна 6. Одна из его
диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
Площадь ромба равна половине произведения его диагоналей. Пусть меньшая из диагоналей равна a, тогда большая равна 3a.
Слайд 10
Задача №9
Найдите меньшую диагональ ромба, стороны которого равны
2, а острый угол равен 60°.
меньшая диагональ ромба лежит
против острого угла. Треугольник ADB равнобедренный. Угол при вершине A равен 60°, значит, треугольник ADB – равносторонний. Диагональ равна 2.
Слайд 12
Задача №11
В ромбе ABCD угол ACD равен 43°. Найдите угол ABC. Ответ дайте
в градусах.
Диагональ ромба AC является биссектрисой угла С, поэтому он равен
86°.Сумма углов B и C равна 180°,поэтому искомый угол B равен 94°. Слайд 13 Задача №12
Найдите большую диагональ ромба, сторона которого равна √3, а острый
угол равен 60°. Тупой угол ромба равен 180°- 60°=120°.
Воспользуемся теоремой косинусов: