Презентация на тему Свойство биссектрисы равнобедренного треугольника

равны, называется равнобедренным треугольником
D

С
E

B
D
A
C


H
M
DM – медиана треугольника АDВ.

DC– биссектриса треугольника АDВ.

DH – высота треугольника DAB. DH AB.

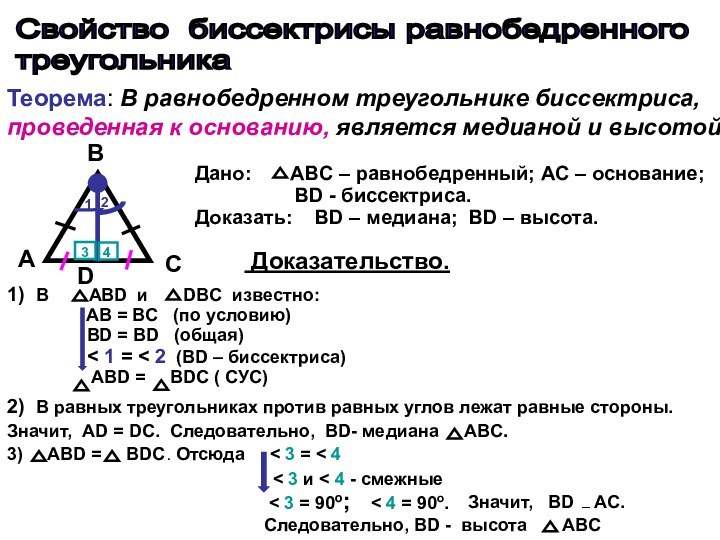
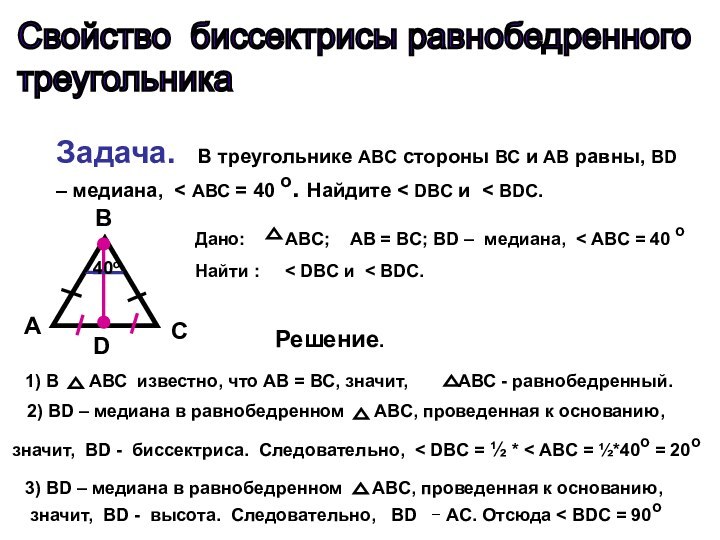
является медианой и высотой.

A
С
B
Дано: ABC –

Доказательство.

1

2

1) В ABD и DBC известно:
AB = BC (по условию)
BD = BD (общая)
< 1 = < 2 (BD – биссектриса)
ABD = ВDС ( СУС)

2) В равных треугольниках против равных углов лежат равные стороны. Значит, АD = DС. Следовательно, BD- медиана ABC.

D

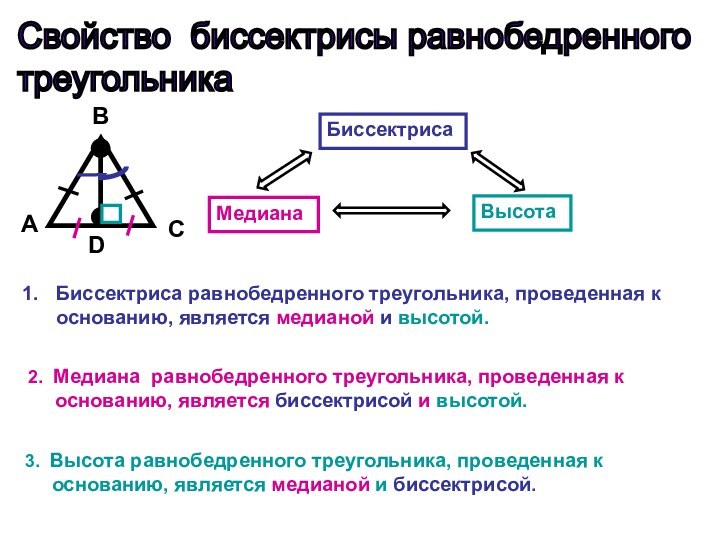
Свойство биссектрисы равнобедренного треугольника

3) ABD = ВDС. Отсюда < 3 = < 4

4

3

< 3 и < 4 - смежные

< 3 = 90о; < 4 = 90о.

Значит, BD AC.

Следовательно, BD - высота ABC

основанию, является медианой и высотой.
2. Медиана равнобедренного треугольника, проведенная

3. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.