- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Точка, прямая, отрезок, луч и угол
Содержание
- 2. Цели и задачи: почему я выбрал эту
- 3. План презентации:1.История геометрии ( в двух частях
- 4. История геометрии. Часть 1.Евклид (ок. 300 до
- 5. История геометрии. Часть 2.Лобачевский, Николай Иванович (1792-1856).Русский
- 6. Точки, прямые и отрезкиПравило: Через любые две
- 7. Точка, прямая и отрезок: провешивание прямой на
- 8. Пересекающиеся и параллельные прямыеСуществуют пересекающиеся и параллельные
- 9. УглыУгол называется развернутым, если обе его стороны
- 10. Скачать презентацию
- 11. Похожие презентации
Цели и задачи: почему я выбрал эту тему?Я считаю, что без точки, прямой, отрезка, луча и угла мы не смогли бы жить. Потому что всё, на что бы не упал наш взгляд , состоит из этих









Слайд 3
План презентации:
1.История геометрии ( в двух частях ).
2.Точка,
прямая и отрезок:
2.1.Провешивание прямой на местности
2.2.Пересекающиеся и параллельные прямые.
3.Луч и угол.
3.1.Смежные и вертикальные углы.
3.2.Градусная мера угла
Слайд 4
История геометрии. Часть 1.
Евклид (ок. 300 до н.э.)
Греческий математик, чей главный труд «Начала» остается основой большей
части современной геометрии. Одна из известных аксиом Евклидовой геометрии гласит: если дана линия и точка вне ее, то через эту точку можно провести только одну линию, параллельную первой. Эту аксиому нельзя доказать, и попытки заменить ее на другую, по которой через точку вне прямой нельзя провести ни одной линии, параллельной данной, или можно провести множество таких линий, привели к созданию в XIX веке так называемых неевклидовых геометрий ( например, геометрии Лобачевского), которые очень важны для многих сторон современной физики.
Слайд 5
История геометрии. Часть 2.
Лобачевский, Николай Иванович (1792-1856).
Русский математик,
предложивший заменить один из главных постулатов геометрии Евклида о
параллельных на аксиому, что в плоскости через точку, лежащую вне прямой, можно провести более одной прямой, не пересекающей первую. Это открытие, не получившее признания современников, совершило затем переворот в представлении о природе пространства и оказало огромное влияние на развитие математического мышления.
Слайд 6
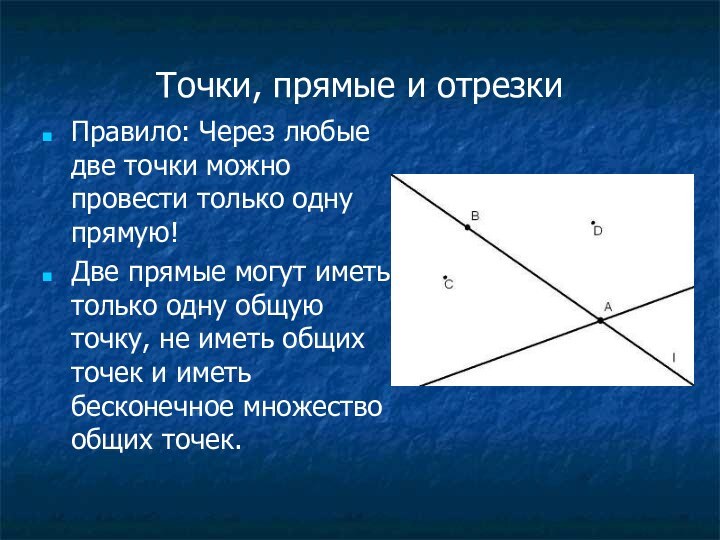
Точки, прямые и отрезки
Правило: Через любые две точки
можно провести только одну прямую!
Две прямые могут иметь только
одну общую точку, не иметь общих точек и иметь бесконечное множество общих точек.
Слайд 7
Точка, прямая и отрезок: провешивание прямой на местности.
Когда-то
перед людьми встала такая задача:
Построить
отрезок большей длины, чем сама вещь, отрезок которой строили.Как вышли из положения:
просто приложили к листу бумаги линейку, отметили какие-нибудь точки A и B и лежащею между ними точку C. Затем они передвинули линейку вправо так, чтобы ее левый конец оказался около точки C, и отметили точку D около правого конца линейки. Такой прием называется провешиванием прямой на плоскости.
Слайд 8
Пересекающиеся и параллельные прямые
Существуют пересекающиеся и параллельные прямые.
Пересекающимися
называют линии, которые имеют хотя бы одну общую
точку.Параллельными прямыми называют линии, не имеющие ни одной общей точки.