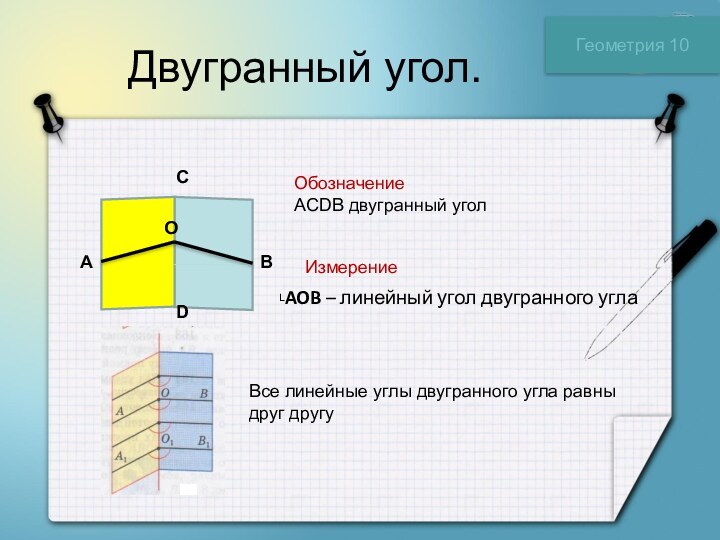
a и двумя полуплоскостями с общей границей a, не
принадлежащими одной плоскости.Прямая a - ребро, полуплоскости, образующие двугранный угол называют гранями
Геометрия 10
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







Геометрия 10
4.Линейный угол двугранного угла равен 800. Найдётся ли в одной из граней угла прямая перпендикулярная другой грани?
5.Угол АВС линейный угол двугранного угла с ребром a, Перпендикулярна ли прямая a плоскости АВС?
6.Верно ли, что все прямые, перпендикулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости?
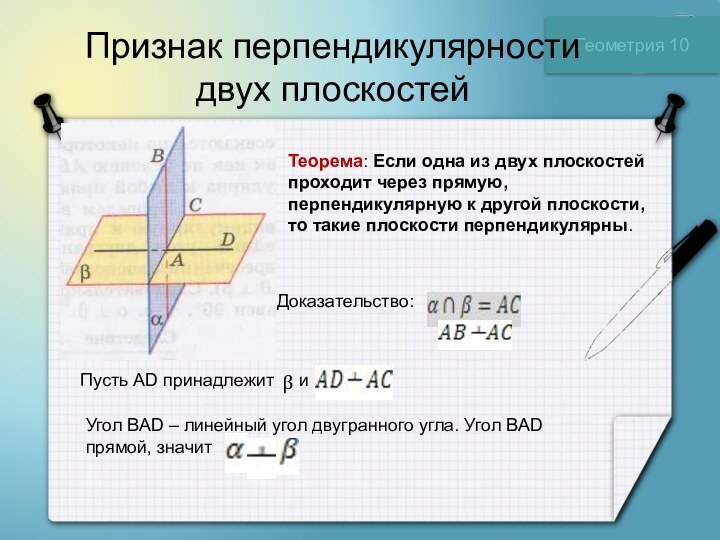
Доказательство:
Пусть АD принадлежит и
β
Угол ВАD – линейный угол двугранного угла. Угол ВАD прямой, значит
При решении задач используют следующие утверждения
Геометрия 10