не параллельны прямой L:
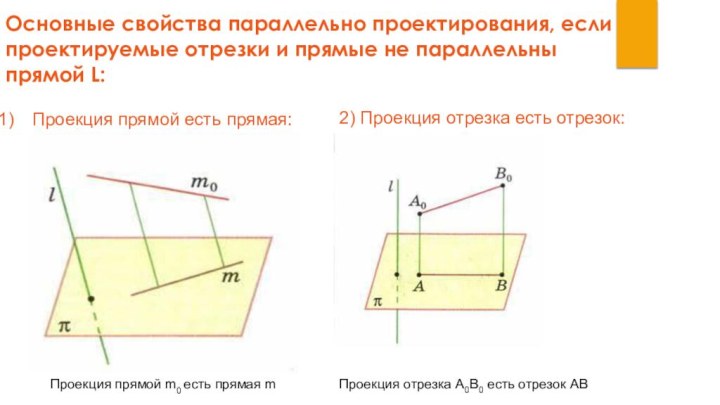
Проекция прямой есть прямая:
Проекция прямой m0
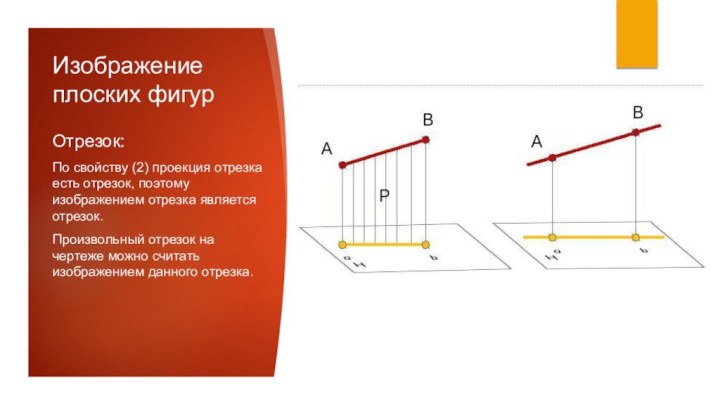
есть прямая m2) Проекция отрезка есть отрезок:
Проекция отрезка А0В0 есть отрезок АВ
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

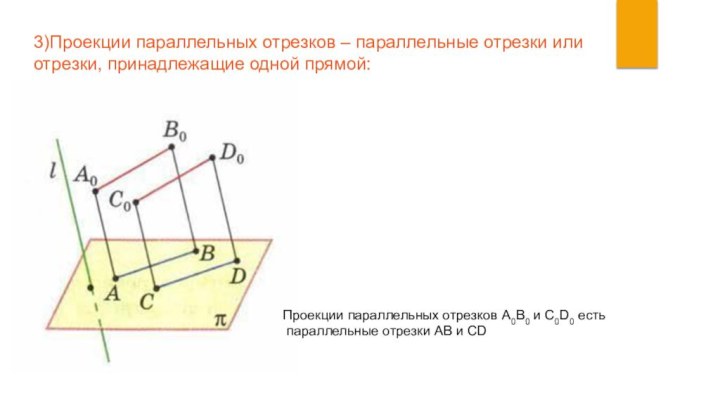

2) Проекция отрезка есть отрезок:
Проекция отрезка А0В0 есть отрезок АВ
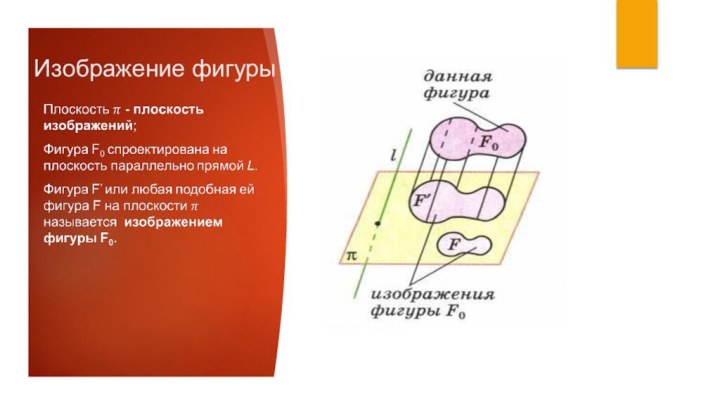
Изображение
плоских фигур
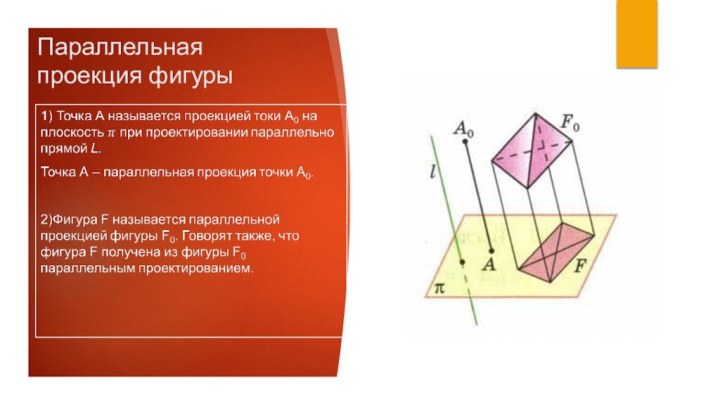
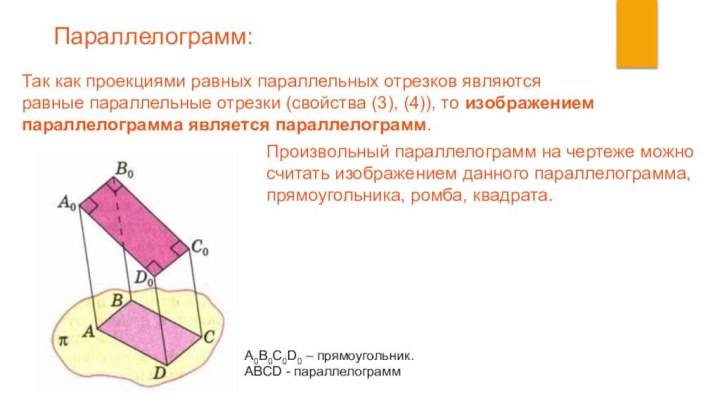
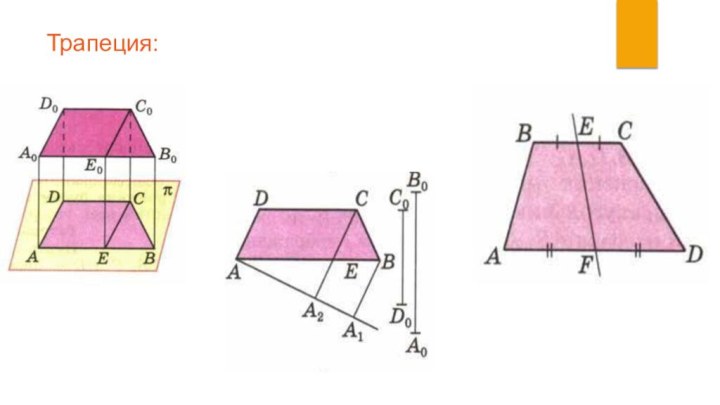
Произвольный параллелограмм на чертеже можно
считать изображением данного параллелограмма,
прямоугольника, ромба, квадрата.
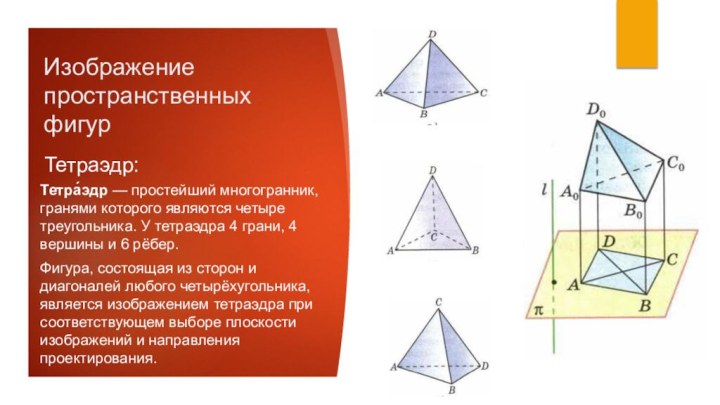
Фигура, состоящая из сторон и диагоналей любого четырёхугольника, является изображением тетраэдра при соответствующем выборе плоскости изображений и направления проектирования.
Изображения остальных рёбер строятся однозначно, т.к. Все грани параллелепипеда являются параллелограммами, и, следовательно, их изображения также будут параллелограммами.