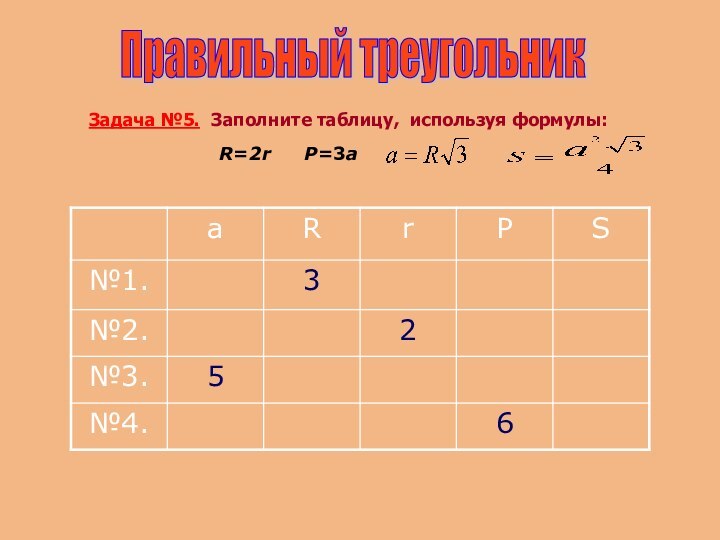
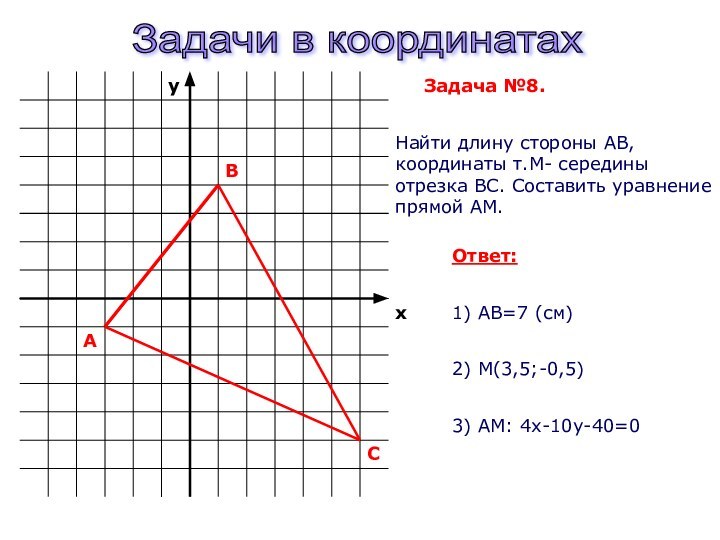
темы : «Треугольник»
Задачи :
1) Рассмотреть различные виды
треугольникаи их свойства.
2) Взаимное расположение треугольника и
окружности.
3) Различные формулы нахождения
элементов треугольника.