Слайд 2
Главная ценность архитектурных сооружений в их красоте. Сооружение
может быть прочным и удобным, но если оно не
привлекает глаз, то оно воспринимается нами как обычное строение, а не как памятник архитектуры.
Задачи работы:
Проанализировать основные особенности использования различных геометрических фигур в нашем городе.
Цель данной работы:
выявить основные геометрические фигуры, используемые в современной архитектуре, и выяснить их происхождение (найти их в объектах).
Слайд 3
Оказывается, играя в «Кубики» мы играем в строителей
и архитекторов, придумываем проекты зданий и строим их. А
куб, параллелепипед, конус и цилиндр чаще всего используются в строительстве. В форме первых двух делают кирпичи и бетонные блоки, из которых возводятся здания, конусы -крыши, цилиндры - колонны.
Слайд 4
Призма
Призма — многогранник, который состоит
из двух плоских равных многоугольников с соответственно параллельными сторонами,
и из отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники называются основаниями призмы, а отрезки, соединяющие соответствующие вершины, — боковыми рёбрами призмы. Все боковые грани призмы — параллелограммы. Объём призмы равен произведению её высоты на площадь основания: V= S * h
Слайд 5
Пирамида
Пирамида - многогранник, основание которого-многоугольник, а остальные грани
— треугольники, имеющие общую вершину. По числу углов основания
различают пирамиды треугольные, четырехугольные и т. д. Объем пирамиды V = 1/3 S * h. Треугольная пирамида является тетраэдром ( четырёхгранником ), четырёхугольная – пятигранником и т.д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани называется апофемой правильной пирамиды.
Слайд 6
Куб
Куб или правильный гексаэдр — правильный многогранник, каждая
грань которого представляет собой квадрат. Частный случай параллелепипеда и
призмы. Куб. -правильный многогранник, у которого грани – квадраты и в каждой вершине сходится по три ребра и три грани. У него: 6 граней, 8 вершин и 12 ребер.
Слайд 7
Параллелепипед
Параллелепипед — призма, основанием которой служит параллелограмм, Различается
несколько типов параллелепипедов. Прямоугольный параллелепипед — это параллелепипед, у
которого все грани прямоугольники; Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники . Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям. Куб — это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба — равные квадраты.
Слайд 8
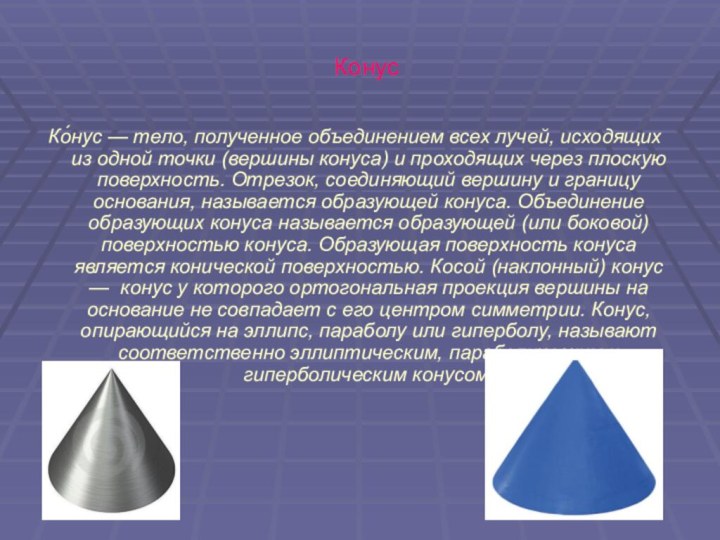
Конус
Ко́нус — тело, полученное объединением всех лучей, исходящих
из одной точки (вершины конуса) и проходящих через плоскую
поверхность. Отрезок, соединяющий вершину и границу основания, называется образующей конуса. Объединение образующих конуса называется образующей (или боковой) поверхностью конуса. Образующая поверхность конуса является конической поверхностью. Косой (наклонный) конус — конус у которого ортогональная проекция вершины на основание не совпадает с его центром симметрии. Конус, опирающийся на эллипс, параболу или гиперболу, называют соответственно эллиптическим, параболическим и гиперболическим конусом.
Слайд 9
Шар
Шар — геометрическое тело; совокупность всех точек пространства,
которые находятся на расстоянии не большем заданного от центра.
Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра. Этот диаметр называется осью шара, а оба конца указанного диаметра — полюсами шара. Поверхность шара называется сферой.
Слайд 10
Цилиндр
Цили́ндр — геометрическое тело, ограниченное цилиндрической поверхностью и
двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность,
получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра. Другая часть, ограниченная параллельными плоскостями, это основания цилиндра. Таким образом граница основания будет по форме совпадать с направляющей.
Слайд 11
Гуляя по городу, рассматривая фотографии из семейного архива,
я искала знакомые фигуры. Обратим внимание, что чаще взгляд
останавливается на зданиях, сочетающих различные геометрические формы
В Самаре это здания драматического театра, филармонии, железнодорожного вокзала, католического костела, православных храмов. В здании Петропавловской церкви Самары, построенной в 1865г. в основании можно увидеть прямой параллелепипед, переходящий в средней части в фигуру, приближающуюся к цилиндру, завершается же она пирамидой. Очень разнообразные фигуры можно встретить в строение различных торговых центрах! А посмотрите на карту нашего города, сколько там параллельных и пересекающихся прямых, окружностей.
Слайд 12
Драматический театр
В этом строении можно встретить усеченные пирамиды,
арки, треугольник, прямоугольники, а также параллельные прямые, которыми украшен
фасад здания
Слайд 13
Филармония
Филармония, на мой взгляд, одно
из самых прекрасных зданий в нашем городе. В его
строении можно встретить геометрические фигуры. Это и окружность, и прямоугольники. Очень много параллельных линий можно встретить на фасаде здания.
Слайд 14
Железнодорожный вокзал
Самарский железнодорожный вокзал является
самым большим в Европе. В нем встречаются самые разнообразные
фигуры. Это и усеченный цилиндр, и пирамиды, и квадраты, и прямоугольники, шаровой сегмент, параллельные и пересекающиеся прямые, различные окружности.
Слайд 15
ТРК Московский
Один из самых посещаемых
торгово-развлекательных центров это, бесспорно, Московский. Шаровой сегмент великолепно смотрится
как украшение для популярного магазина, кроме этого в фасаде здания можно наблюдать прямоугольники, параллельные прямые.