- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойство срединного перпендикуляра
Содержание
- 2. Этапы урока: организационный;этап проверки домашнего задания;актуализация знаний учащихся;объяснение нового материала;закрепление;проверка усвоения.Тип урока: усвоение новых знаний
- 3. Рассмотреть теорему о серединном перпендикуляре и
- 4. Признаки равенства треугольниковПризнаки равенства прямоугольных треугольниковРасстояние от точки до прямойПовторение (устный опрос ):
- 5. • точка пересечения медиан; • точка пересечения
- 6. Серединным перпендикуляром к отрезку называется прямая, проходящая
- 7. Каждая точка серединного перпендикуляра к
- 8. Каждая точка, равноудаленная от концов
- 9. Следствие: Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке
- 10. ДоказательствоДано: mAB, nBC, AM=MB, CN=NB. Прямые m
- 11. Проверка первичного усвоения (решение задач по готовым
- 12. Домашнее задание П. 75 (стр. 174)Задачи 682, 684
- 13. Скачать презентацию
- 14. Похожие презентации
Этапы урока: организационный;этап проверки домашнего задания;актуализация знаний учащихся;объяснение нового материала;закрепление;проверка усвоения.Тип урока: усвоение новых знаний












Слайд 2
Этапы урока:
организационный;
этап проверки домашнего задания;
актуализация знаний учащихся;
объяснение
нового материала;
Слайд 3 Рассмотреть теорему о серединном перпендикуляре и её
следствие.
Ввести понятие серединного перпендикуляра к отрезку.
Формировать умения применять
известные знания в незнакомой ситуации, сравнивать, анализировать, обобщать.Цели урока:
Слайд 4
Признаки равенства треугольников
Признаки равенства прямоугольных треугольников
Расстояние от точки
до прямой
Повторение (устный опрос ):
Слайд 5
• точка пересечения медиан;
• точка пересечения биссектрис;
• точка пересечения серединных перпендикуляров;
• точка пересечения высот.
C каждым треугольником связаны четыре точки):
Эти четыре точки называют замечательными точками треугольника.
Слайд 6 Серединным перпендикуляром к отрезку называется прямая, проходящая через
середину данного отрезка и перпендикулярная к нему
Серединный перпендикуляр
A
a
B
O
Слайд 7 Каждая точка серединного перпендикуляра к отрезку
равноудалена от концов этого отрезка
Теорема
Дано: М - произвольная
точка на а, где а - серединный перпендикуляр к отрезку АВ.Доказать: МА=МВ
Доказательство:
Если М АВ, то М совпадает с
точкой О, значит МА=МВ.
2) Если М АВ, то АМО= ВМО по двум катетам (АО=ВО, МО- общий катет), откуда получаем МА=МВ
Слайд 8 Каждая точка, равноудаленная от концов этого
отрезка, лежит на серединном перпендикуляре к нему
Обратно
Дано: N равноудалена
от концов отрезка AB, NА=NВ, прямая m – серединный перпендикуляр к отрезку АВДоказать: N – лежит на прямой m
Доказательство:
1) Пусть N АВ, тогда N совпадает с O, и N лежит на прямой m.
2) Пусть N АВ, тогда АNО равнобедренный, т.к. AN=BN. Отрезок NO – медиана этого треугольника, а значит, и высота. Тогда NOAB. Через точку О к прямой АВ можно провести только один серединный перпендикуляр, т.е. NO и m совпадают и N – точка на m.
А
N
B
O
m
Слайд 10
Доказательство
Дано:
mAB, nBC, AM=MB, CN=NB. Прямые m и
n пересекаются в некоторой точке О
Доказать: Точка O
является точкой пересечения прямых m, n и p.Доказательство:
1) Предположим: m║n, тогда: ABm и ABn, что невозможно.
2) По доказанной теореме:
OB=OA и OC=OB, откуда
OA=OС, т.е. точка O равноудалена от концов отрезка AC и, значит, лежит на срединном перпендикуляре p к этому отрезку.
Следовательно: O= m n p.
Слайд 11
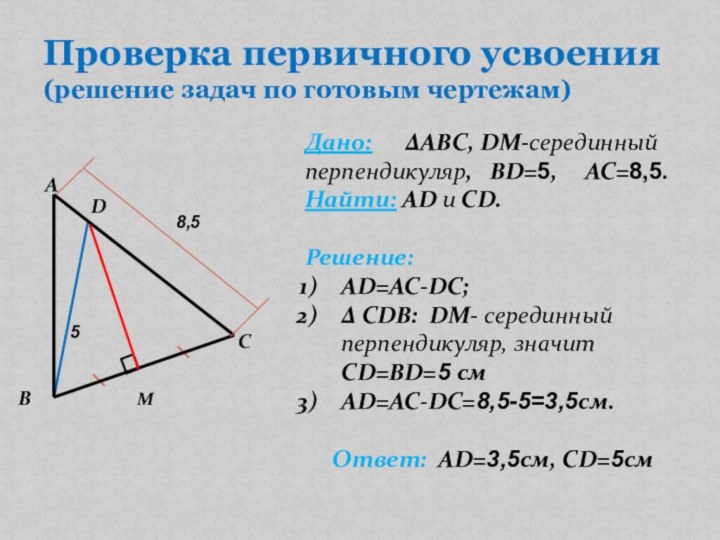
Проверка первичного усвоения
(решение задач по готовым чертежам)
Дано:
ΔABC, DM-серединный перпендикуляр, BD=5,
AC=8,5.Найти: AD и CD.
Решение:
АD=AC-DС;
Δ CDB: DM- серединный перпендикуляр, значит CD=BD=5 см
АD=AC-DС=8,5-5=3,5см.
Ответ: АD=3,5см, CD=5см