- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Признаки параллелограмма
Содержание
- 2. Задачи урока:
- 3. АBCDAB CD, AC BD ОпределениеЧетырехугольник, у которого противоположные стороны попарно параллельны, называется параллелограммом
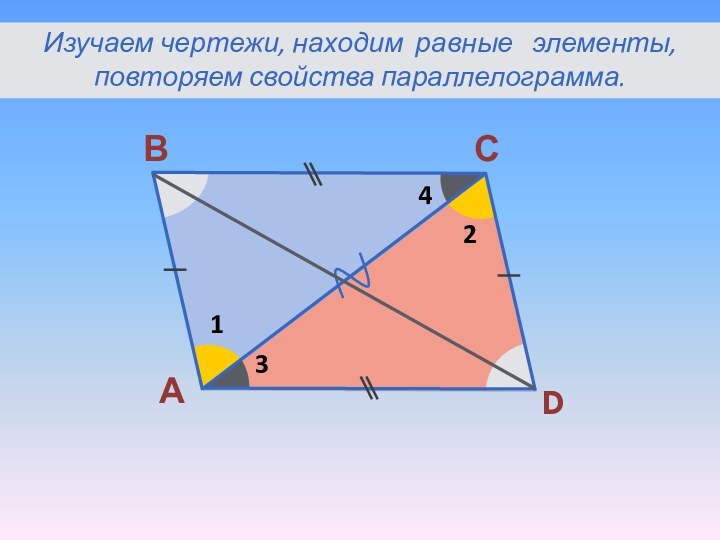
- 4. АВСD1234Изучаем чертежи, находим равные элементы, повторяем свойства параллелограмма.
- 5. Среди четырехугольников есть параллелограммы?
- 6. АВСАВ, ВС - боковые стороны равнобедренного треугольникаА,
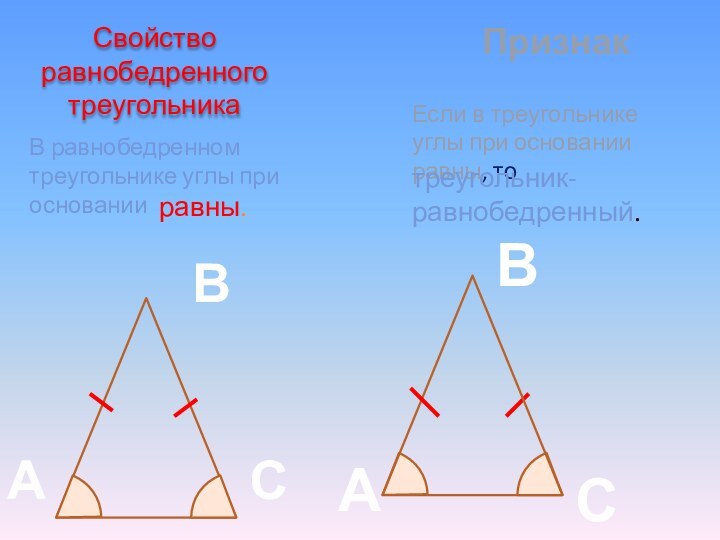
- 7. Свойство равнобедренного треугольникаВСВ равнобедренном треугольнике углы при
- 8. СвойствоПризнак?Обратная теоремаОпределение
- 9. Сумма смежных углов180˚Сумма углов 180 ˚ -Прямое утверждение:Обратное утверждение: углы смежные
- 10. В параллелограмме противоположные стороны равны.Если в четырехугольнике противоположные стороны равны, то этот четырехугольник параллелограмм.
- 11. 2°. Если AB=CD и BC=AD, то ABCD-параллелограмм. АBCДано:ABCD –четырехугольник. AB=CD и BC=AD.Доказать, что ABCD-параллелограмм.D
- 12. В параллелограмме диагонали точкой пересечения делятся
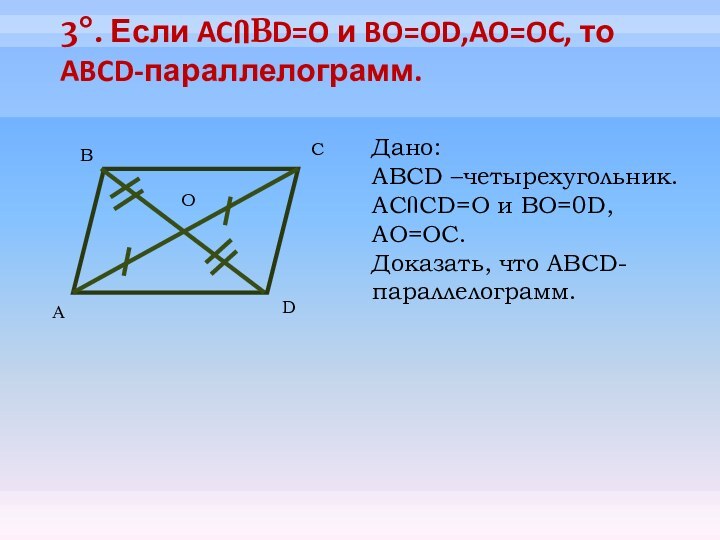
- 13. 3°. Если ACՈBD=O и BO=OD,AO=OC, то ABCD-параллелограмм. АBCDДано:ABCD –четырехугольник. ACՈCD=O и BO=0D, AO=OC.Доказать, что ABCD-параллелограмм.O
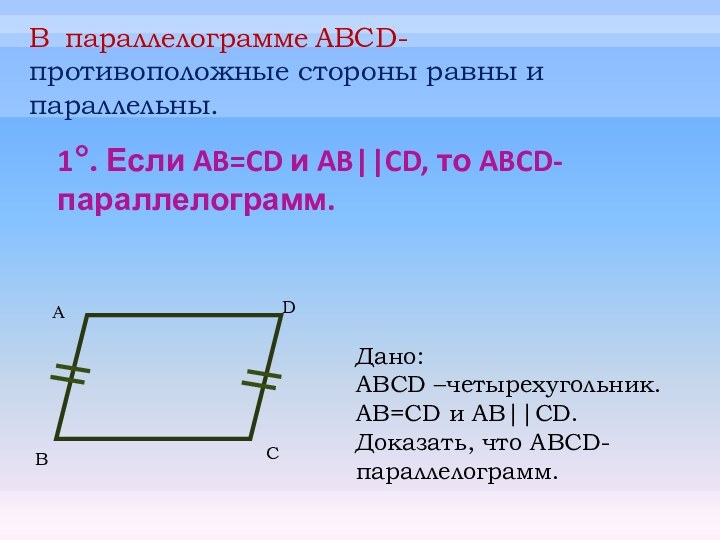
- 14. 1°. Если AB=CD и AB||CD, то ABCD-параллелограмм.
- 15. Признаки параллелограммаПротивоположные стороны равныПротивоположные стороны параллельныДиагонали параллелограмма точкой пересечения делятся пополам
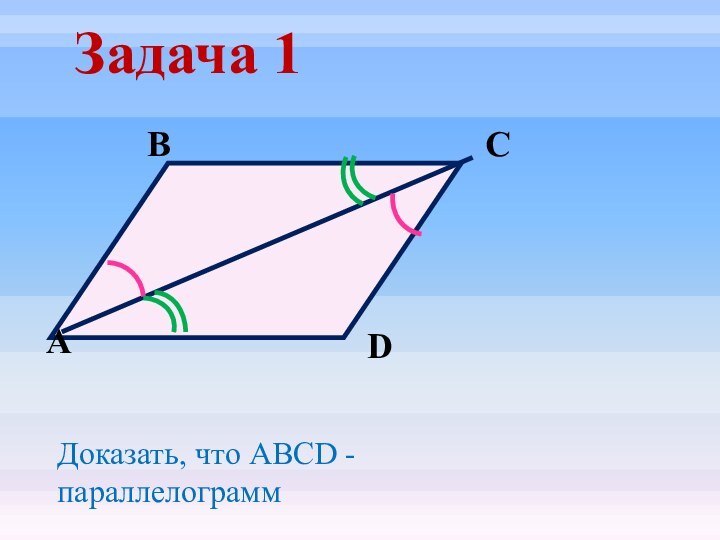
- 16. Задача 1DСВАДоказать, что ABCD - параллелограмм
- 17. Задача 1DСВАДоказать, что ABCD - параллелограмм
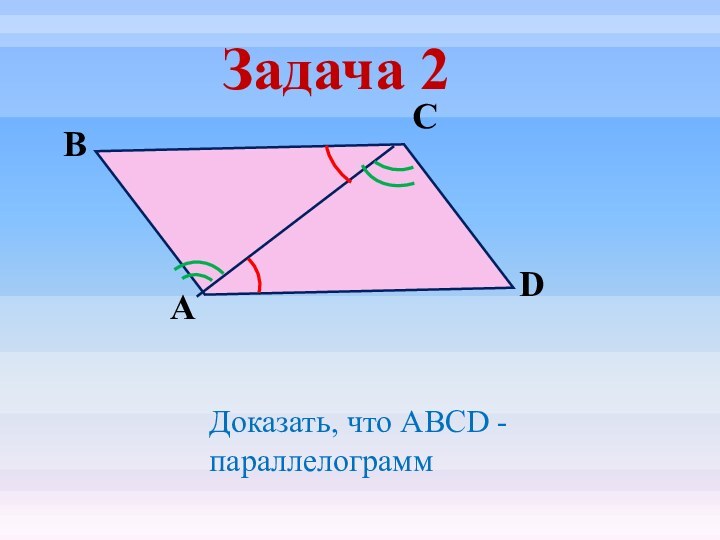
- 18. Задача 2DСВАДоказать, что ABCD - параллелограмм
- 19. Задача 2DСВАДоказать, что ABCD - параллелограмм
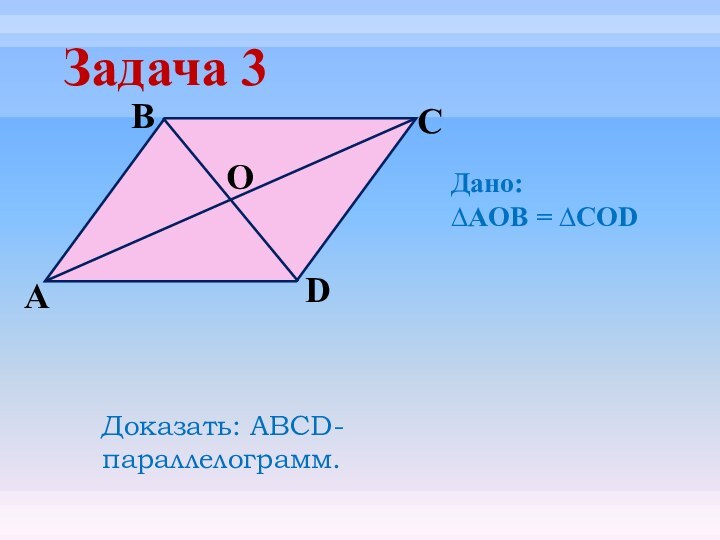
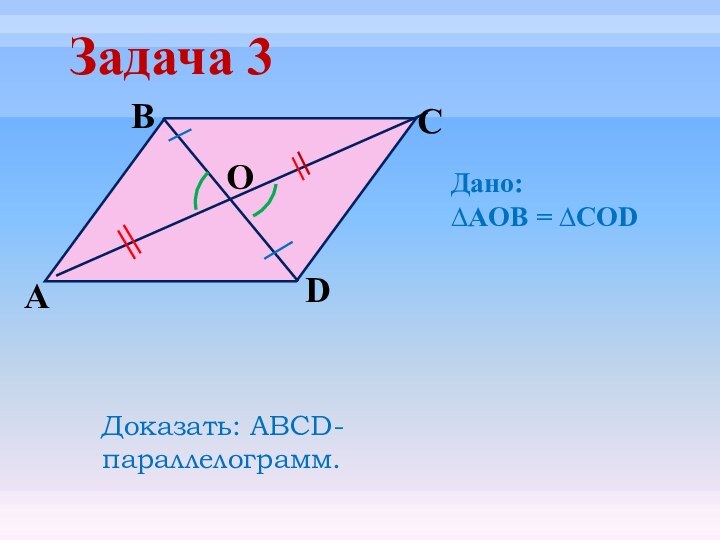
- 20. Задача 3ODCBАДоказать: АВСD- параллелограмм.Дано:∆AOB = ∆COD
- 21. Задача 3ODCBАДоказать: АВСD- параллелограмм.Дано:∆AOB = ∆COD
- 22. Посмотри, как можно построить параллелограмм, используя свойства его диагоналей.
- 23. Скачать презентацию
- 24. Похожие презентации
Задачи урока:













Слайд 3
А
B
C
D
AB CD, AC BD
Определение
Четырехугольник, у которого противоположные
стороны попарно параллельны, называется параллелограммом
Слайд 6
А
В
С
АВ, ВС - боковые стороны равнобедренного треугольника
А, С
– углы при основании равнобедренного треугольника
АС - основание равнобедренного
треугольникаТреугольник называется
равнобедренным,
если две его стороны равны





























