- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Элементарные процессы роста кристаллов (лекция 2)
Содержание
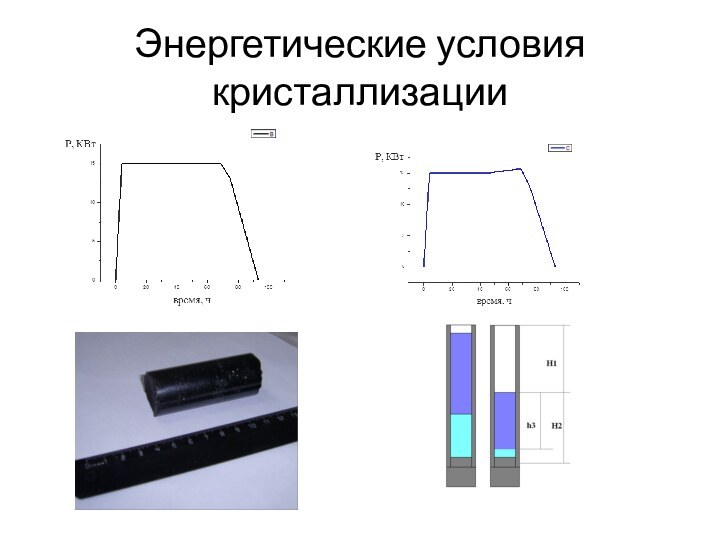
- 2. Энергетические условия кристаллизацииΔТ = Т0 – Т
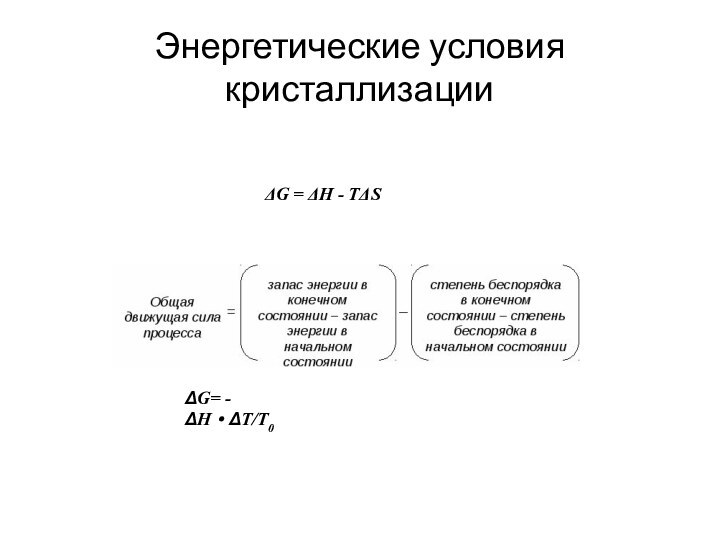
- 3. Энергетические условия кристаллизацииΔG = ΔH - TΔSΔG= - ΔH·ΔT/T0
- 4. Энергетические условия кристаллизацииGж=Gкр → Tпл ∆G=Gж-тв∆T=Tпл–T кр - степень переохлажденияΔG= - ΔH·ΔT/T0
- 5. Энергетические условия кристаллизацииΔT=T-T0 - переохлаждениеΔP=P-P0 – пересыщениеΔс=с-с0 - пересыщение
- 6. Энергетические условия кристаллизацииФазовая диаграмма кристалл-пар(кристалл-раствор) P – T(C-T) диаграмма
- 7. Энергетические условия кристаллизацииФаза – однородная часть,
- 8. Эвтектика греч. éutektos — легкоплавящийся) — нонвариантная
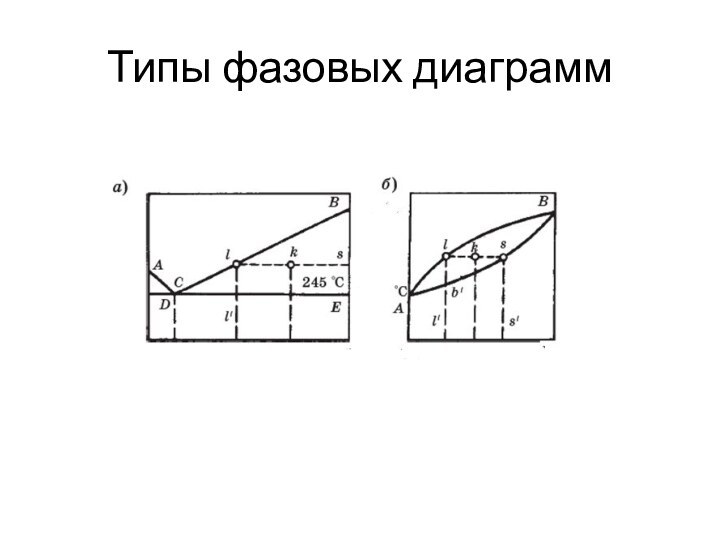
- 9. Типы фазовых диаграмм
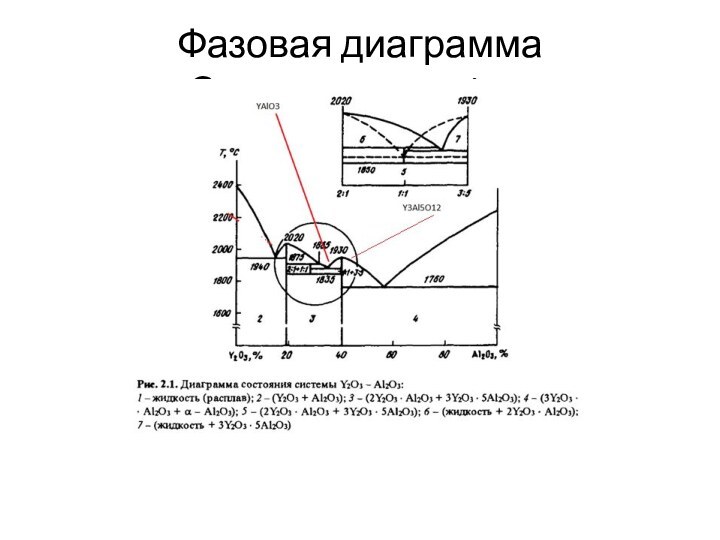
- 10. Фазовая диаграмма Системы Y2O3-Al2O3
- 11. Кинетика кристаллизацииГиббс – теория зарождения центров кристаллизации.
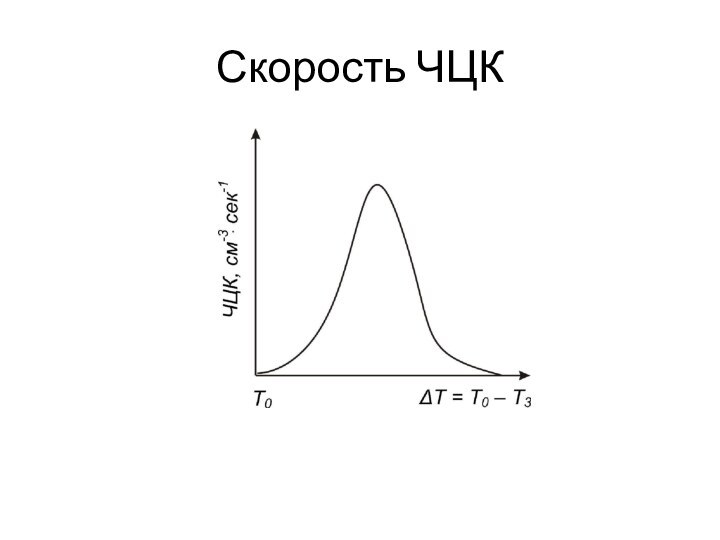
- 12. Скорость ЧЦК
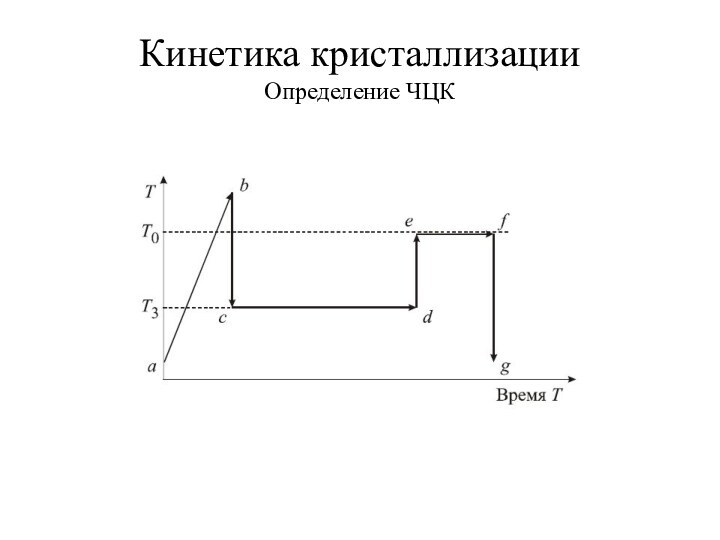
- 13. Кинетика кристаллизации Определение ЧЦК
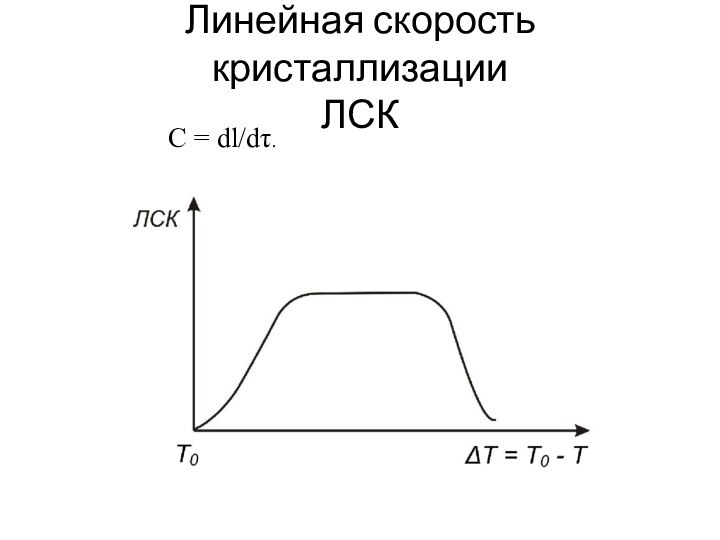
- 14. Линейная скорость кристаллизации ЛСКС = dl/dτ.
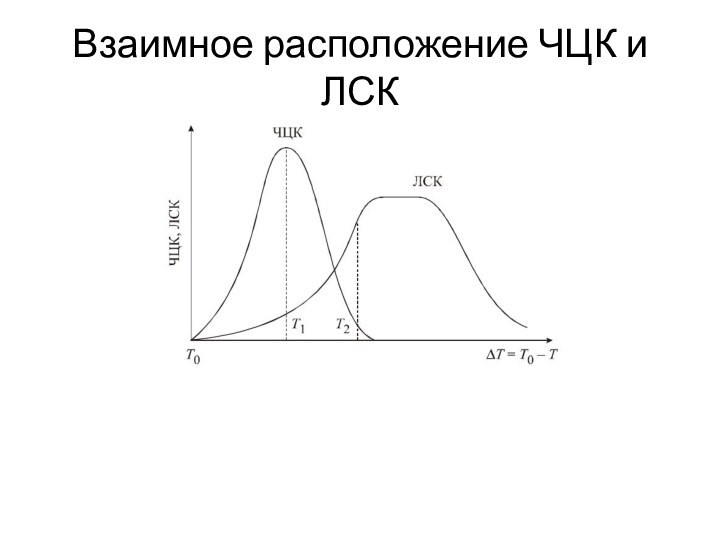
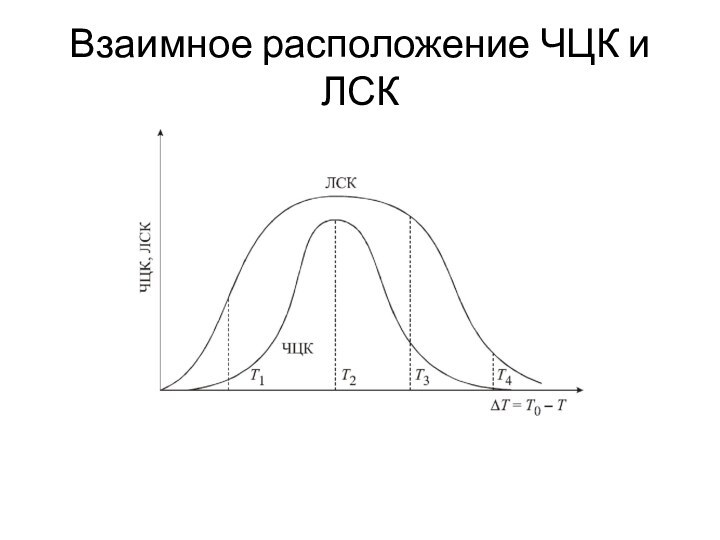
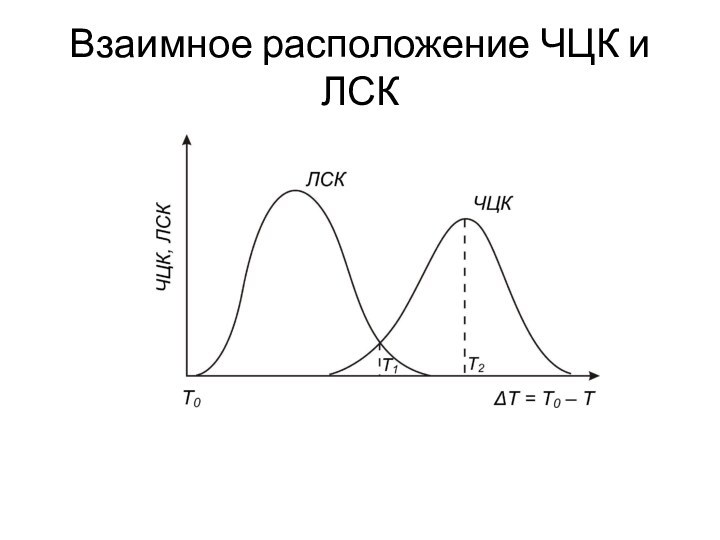
- 15. Взаимное расположение ЧЦК и ЛСК
- 16. Взаимное расположение ЧЦК и ЛСК
- 17. Взаимное расположение ЧЦК и ЛСК
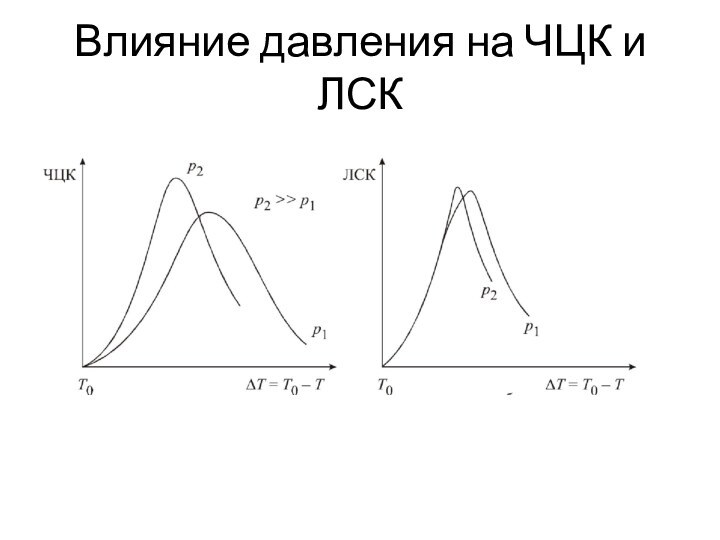
- 18. Влияние давления на ЧЦК и ЛСК
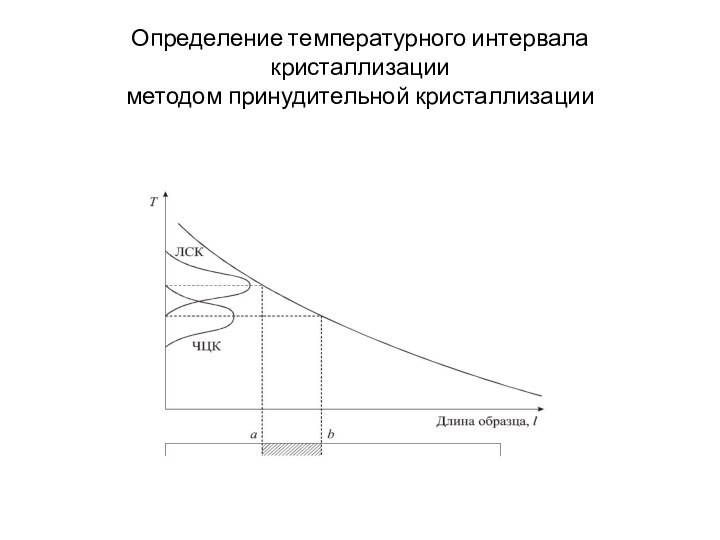
- 19. Определение температурного интервала кристаллизации методом принудительной кристаллизации
- 20. Суммарная(объемная) скорость кристаллизации v =f(τ,T,c,J,b)V=8l3При c = dl/dτ =l/τ= const, T=constv = dV/dτ = 24 c3τ2
- 21. Огранка кристалла и скорость роста граней Vc>Vb>VaVc
- 22. Огранка кристалла и скорость роста граней Геометрический отбор Методы Бриджмана, Обреимова-Шубникова, Стокбаргера
- 23. Огранка свободно растущего кристаллаV11/V01≥√¯2V11/V01≤√¯2/2√¯2/2
- 24. Огранка свободно растущего кристалла
- 25. Огранка свободно растущего кристалла
- 26. Огранка кристалловРеальный кристалл сложен пирамидами роста. Пирамиды
- 27. Огранка кристалловГрани реальные физически возможные физически невозможные
- 28. Огранка кристалловОбъемноцентрированая решетка. Максимальная ретикулярная плотность для грани [110]
- 29. Огранка кристалловГранецентрированная решетка . Максимальная ретикулярная плотность для грани [110]
- 30. Огранка кристалловФорм роста много Равновесная форма кристалла
- 31. Огранка кристаллов Принцип Гиббса-Вульфа- КюриПринцип Гиббса-Вульфа-Кюри. Равновесная
- 32. Теорема Вульфаσi/hi = constВ равновесном кристалле расстояния
- 33. Метод Шубникова определения равновесной формы кристаллаС медленно
- 34. Элементарные процессы роста кристалловГрань не являющаяся плотноупакованной
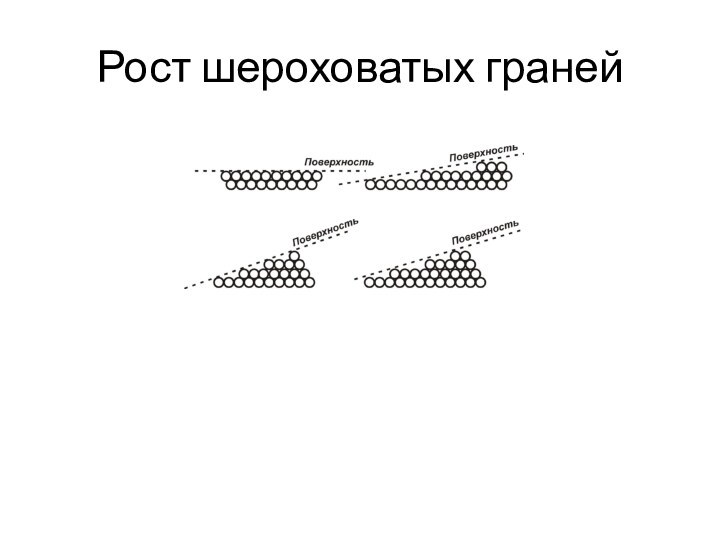
- 35. Рост шероховатых граней
- 36. Элементарные процессы роста кристалловF- гладкие граниK,S –
- 37. Рост атомарно гладких гранейКонцепция образовании двумерных зародышейГиббсом,
- 38. Дислокационный механизм роста гладких гранейВинтовые дислокации Франк,
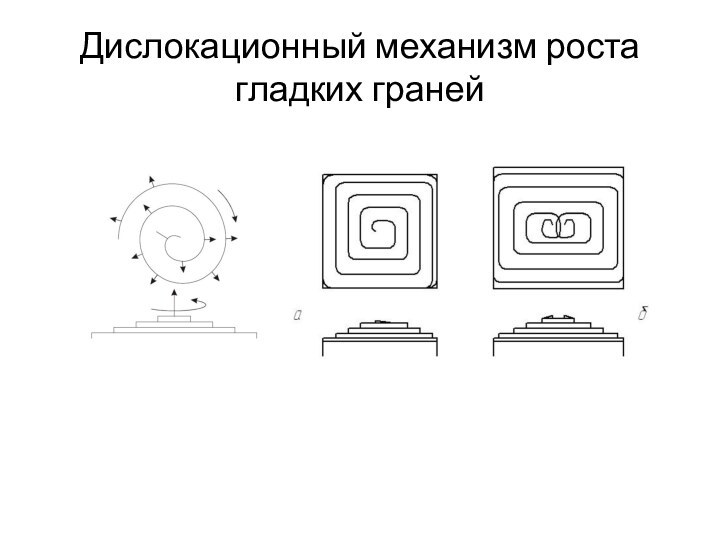
- 39. Дислокационный механизм роста гладких граней
- 40. Установка «Гранат-2», компоненты теплового узла и Компоненты
- 41. Монокристалл алюмо-иттриевого граната, легированного ванадием
- 42. Срезы були алюмоиттриевого граната с ванадием а,б,в
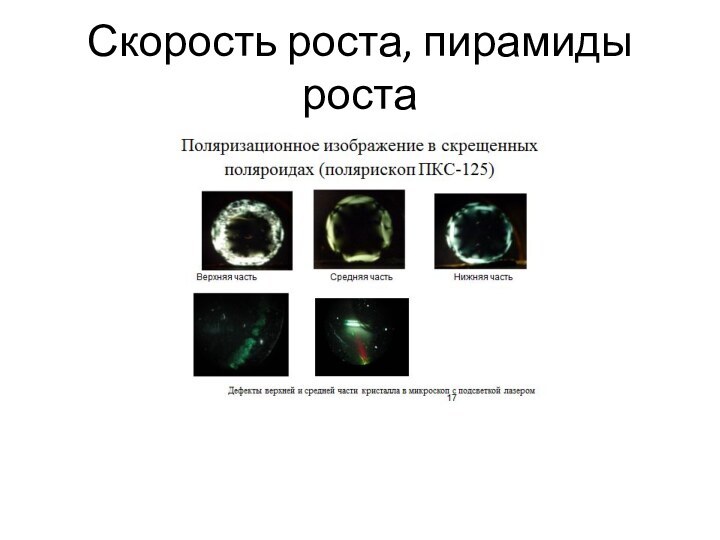
- 43. Скорость роста, пирамиды роста
- 44. Свойства кристаллов соединений Al2O3-Y2O3
- 45. Скачать презентацию
- 46. Похожие презентации
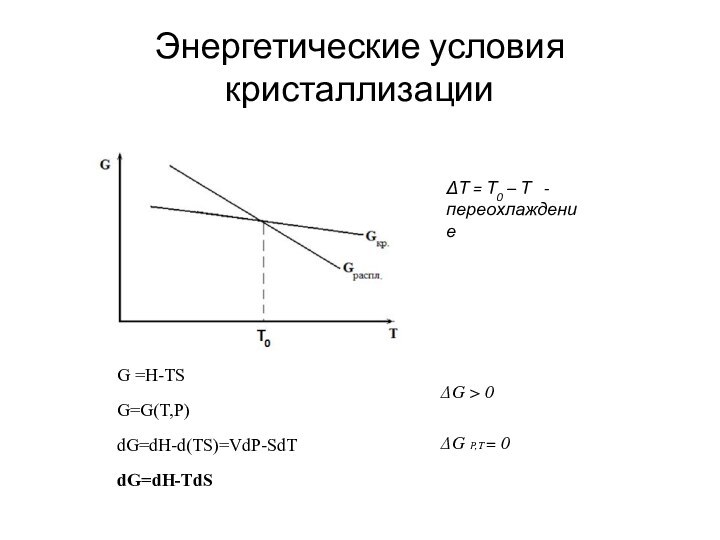
Энергетические условия кристаллизацииΔТ = Т0 – Т - переохлаждение G =H-TS G=G(T,P) dG=dH-d(TS)=VdP-SdTdG=dH-TdSΔG > 0ΔG P,T = 0







![Элементарные процессы роста кристаллов (лекция 2) Огранка кристалловОбъемноцентрированая решетка. Максимальная ретикулярная плотность для грани [110]](/img/tmb/15/1442897/120d082efad36be71e7407c039b9e25a-720x.jpg)
![Элементарные процессы роста кристаллов (лекция 2) Огранка кристалловГранецентрированная решетка . Максимальная ретикулярная плотность для грани [110]](/img/tmb/15/1442897/f205ef06ed6230aec5d67b80e68f56f9-720x.jpg)








Слайд 4
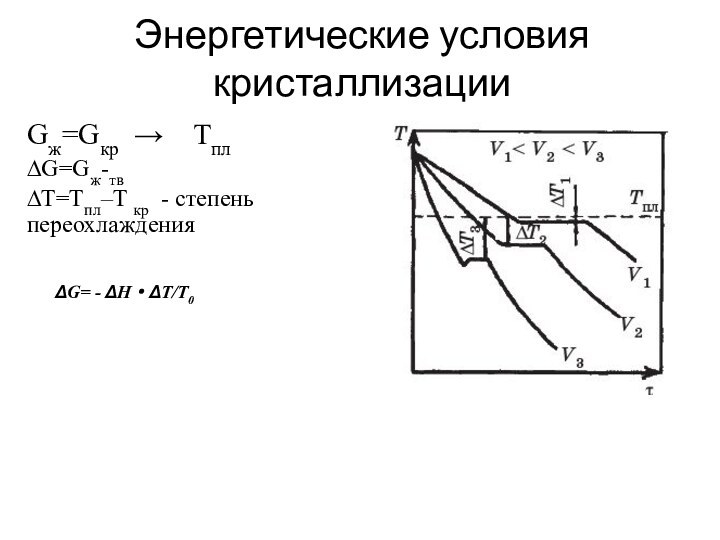
Энергетические условия кристаллизации
Gж=Gкр → Tпл
∆G=Gж-тв
∆T=Tпл–T кр
- степень переохлаждения
ΔG= - ΔH·ΔT/T0
Слайд 5
Энергетические условия кристаллизации
ΔT=T-T0 - переохлаждение
ΔP=P-P0 – пересыщение
Δс=с-с0 -
пересыщение
Слайд 6
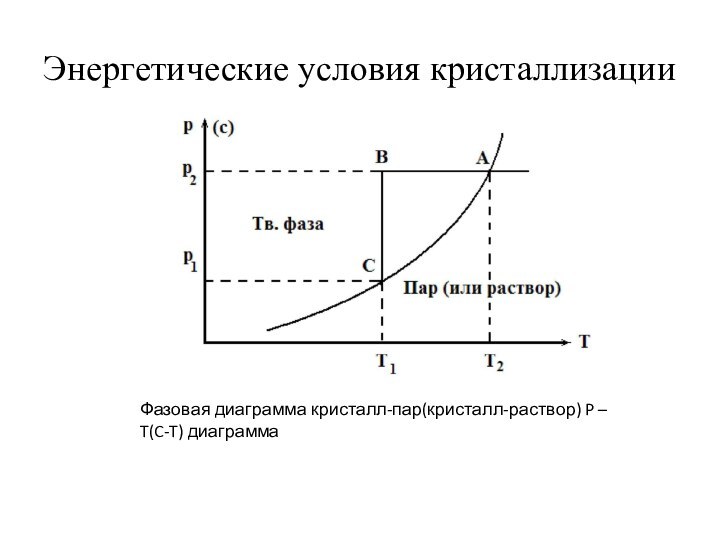
Энергетические условия кристаллизации
Фазовая диаграмма кристалл-пар(кристалл-раствор) P – T(C-T)
диаграмма
Слайд 7
Энергетические условия кристаллизации
Фаза – однородная часть, характеризующаяся
определенным составом, кристаллической решеткой и отделенная от других частей
поверхностью разделаТермодинамическая степень свободы - число переменных - С (T, P, концентрация компонентов)
Правило фаз Гиббса :
с=n+p-f
P=1 (T)
Для двойных систем f=3 – максимально возможное кол. Фаз.
Слайд 8
Эвтектика греч. éutektos — легкоплавящийся) — нонвариантная (при
постоянном давлении) точка в системе из n компонентов, в
которой находятся в равновесии n твердых фаз и жидкая фазаЭвтектическая точка
Слайд 11
Кинетика кристаллизации
Гиббс – теория зарождения центров кристаллизации.
Переход
из неравновесного(метастабильного) состояния
Метастабильное состояние – появление зародышей.
Создание
поверхности раздела фаз. Требует затрат свободной энергии до достижении зародышей определенного размера.Скорость зарождения центров кристаллизации (ЧЦК)
2. Линейная скорость кристаллизации (ЛСК)
3. Объемная скорость кристаллизации
J=C·exp (-ΔGc/RT)
Слайд 20
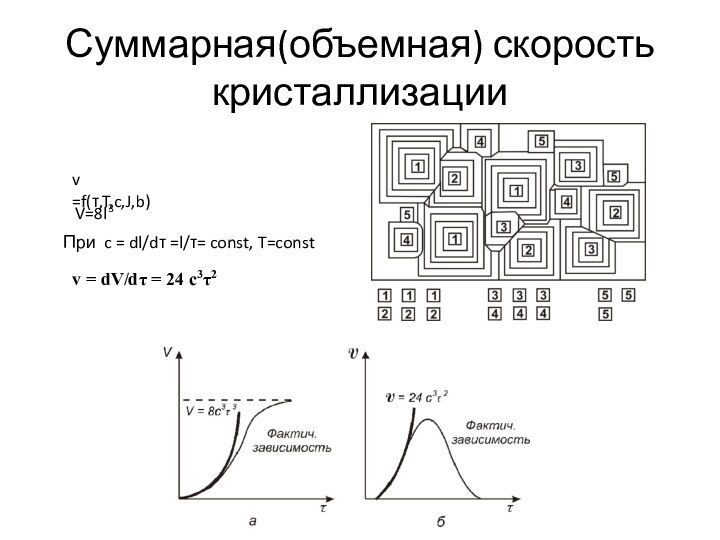
Суммарная(объемная) скорость кристаллизации
v =f(τ,T,c,J,b)
V=8l3
При c = dl/dτ
=l/τ= const, T=const
v = dV/dτ = 24 c3τ2
Слайд 21
Огранка кристалла и скорость роста граней
Vc>Vb>Va
Vc : Va
= 3
Анизотропия скорости роста кристалла в различных кристаллографических направлениях
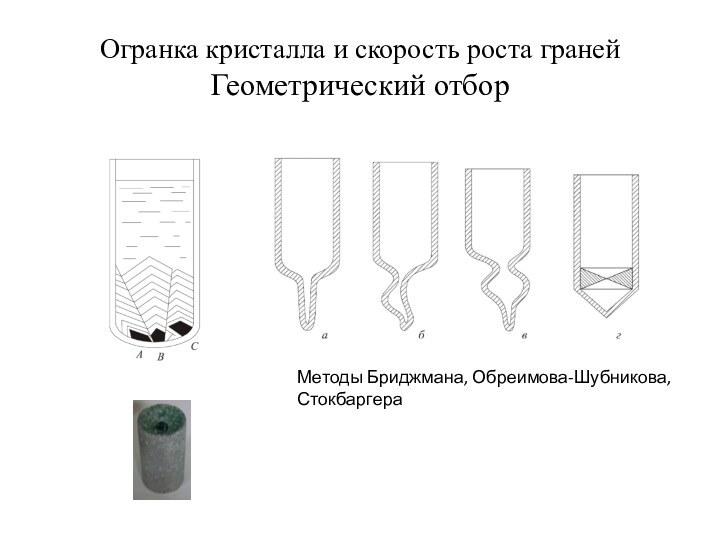
лежит в основе явления геометрического отбора (конкурирующего роста). Слайд 22 Огранка кристалла и скорость роста граней Геометрический отбор
Методы Бриджмана, Обреимова-Шубникова, Стокбаргера
Слайд 23
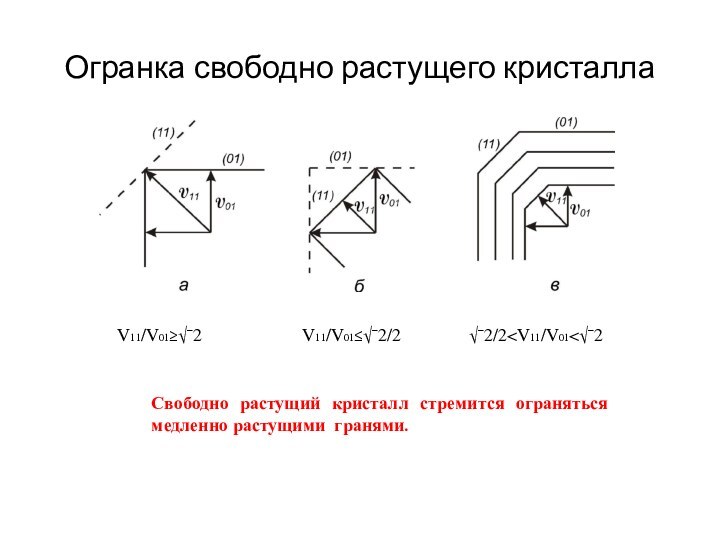
Огранка свободно растущего кристалла
V11/V01≥√¯2
V11/V01≤√¯2/2
√¯2/2
медленно растущими гранями.
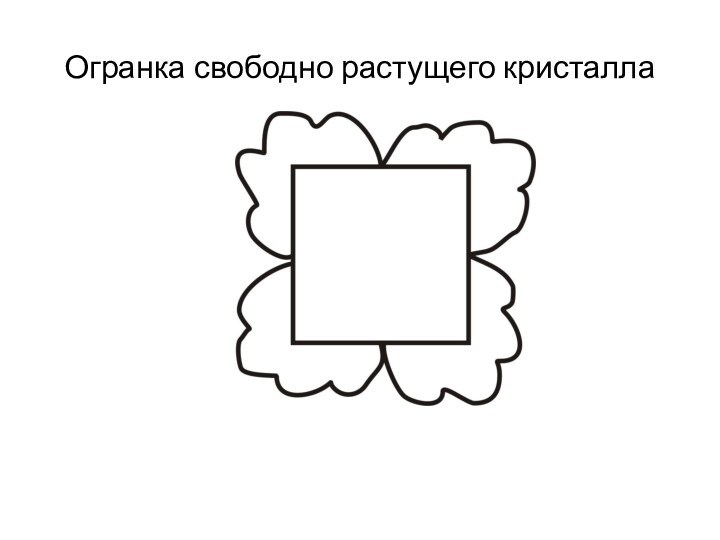
Слайд 26
Огранка кристаллов
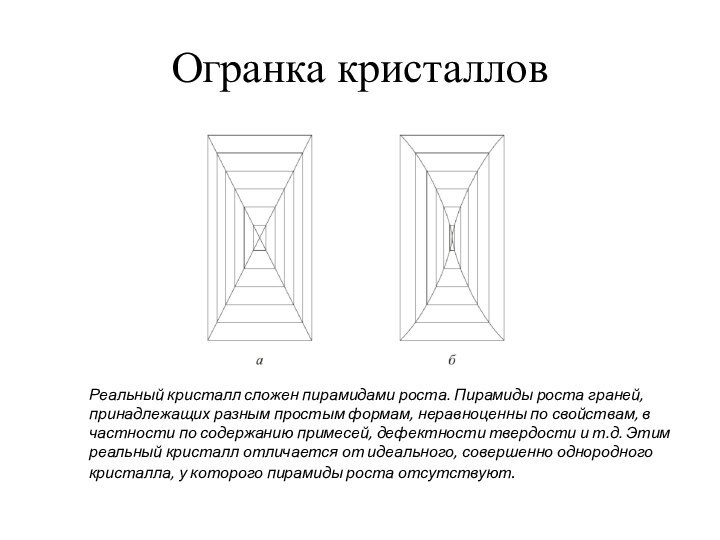
Реальный кристалл сложен пирамидами роста. Пирамиды роста
граней,
принадлежащих разным простым формам, неравноценны по свойствам, в
частности по
содержанию примесей, дефектности твердости и т.д. Этимреальный кристалл отличается от идеального, совершенно однородного
кристалла, у которого пирамиды роста отсутствуют.
Слайд 27
Огранка кристаллов
Грани реальные
физически возможные
физически невозможные
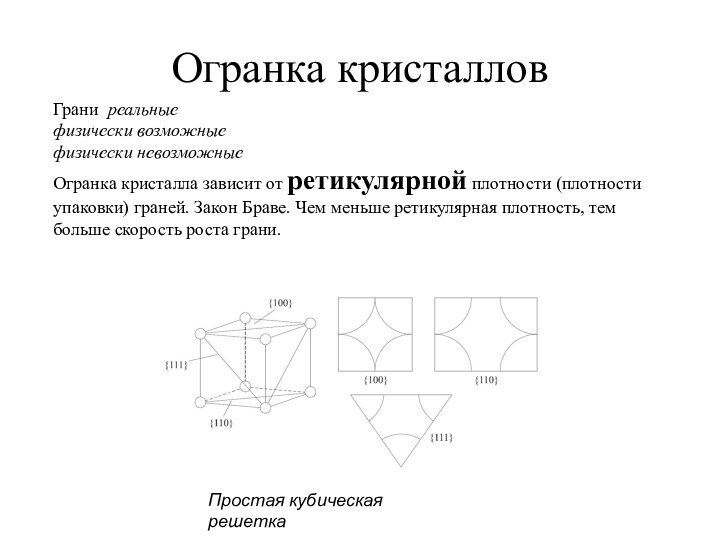
Огранка
кристалла зависит от ретикулярной плотности (плотности упаковки) граней. Закон
Браве. Чем меньше ретикулярная плотность, тем больше скорость роста грани.Простая кубическая решетка
Слайд 28
Огранка кристаллов
Объемноцентрированая решетка.
Максимальная ретикулярная плотность для грани
[110]
Слайд 29
Огранка кристаллов
Гранецентрированная решетка . Максимальная ретикулярная плотность для
грани [110]
Слайд 30
Огранка кристаллов
Форм роста много
Равновесная форма кристалла одна
. Образована плотноупакованным гранями
Пример. Алмаз.Равновесная форма - октаэдр
Формы
роста - I) октаэдр, 2) ромбододекаэдр,3) куб, 4) комбинации (октаэдра, куба, додекаэдра)
Слайд 31
Огранка кристаллов
Принцип Гиббса-Вульфа- Кюри
Принцип Гиббса-Вульфа-Кюри. Равновесная форма кристалла
соответствует минимуму свободной объемной и поверхностной энергиией
ΣσiSi=min (V=const)
Для реальных
кристаллов объемная энергия не является постоянной и зависит от дефектности кристалла
Слайд 32
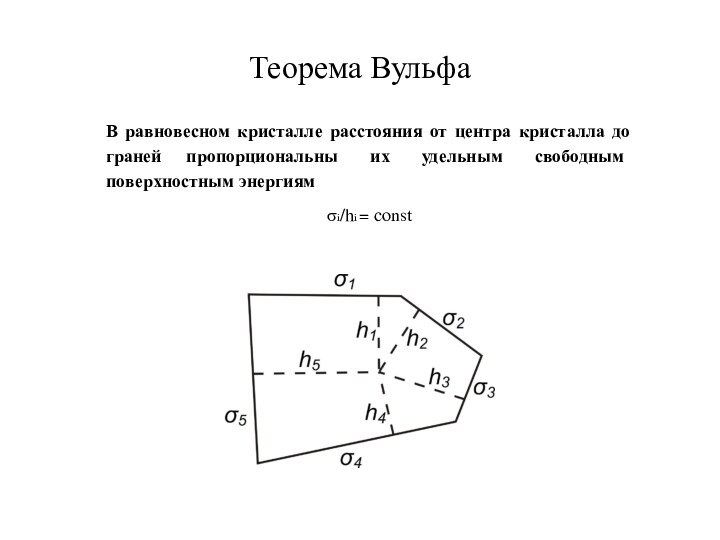
Теорема Вульфа
σi/hi = const
В равновесном кристалле расстояния от
центра кристалла до граней пропорциональны их удельным свободным поверхностным
энергиям
Слайд 33
Метод Шубникова определения равновесной формы кристалла
С медленно растущих
граней, принадлежащих равновесной, форме, при растворении удаляется больше вещества,
чем возвращается обратно при охлаждении раствора. Избыток осаждается на остальных гранях, которые в результате растут быстрее и зарастают, исчезая из огранки кристалла.Равновесная форма кристалла не изменяется при колебаниях температуры
Слайд 34
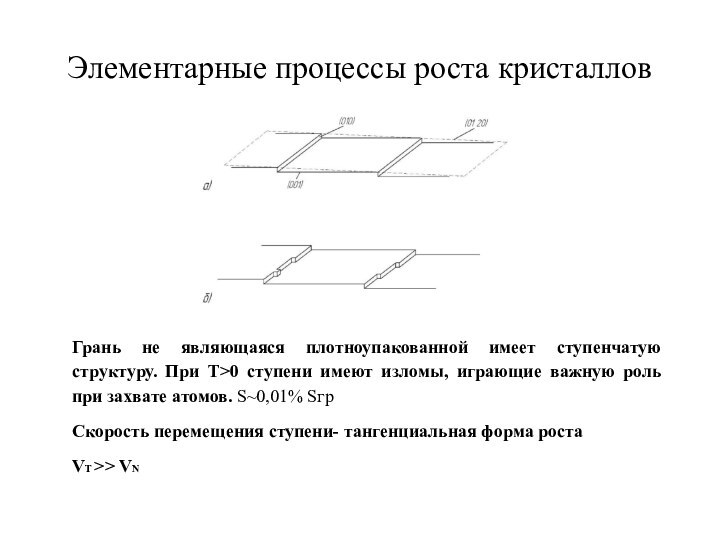
Элементарные процессы роста кристаллов
Грань не являющаяся плотноупакованной имеет
ступенчатую структуру. При T>0 ступени имеют изломы, играющие важную
роль при захвате атомов. S~0,01% SгрСкорость перемещения ступени- тангенциальная форма роста
VT >> VN
Слайд 36
Элементарные процессы роста кристаллов
F- гладкие грани
K,S – шероховатые
грани
Скорость роста для шероховатых граней существенно больше чем гладких(плотноупаковочных)
Слайд 37
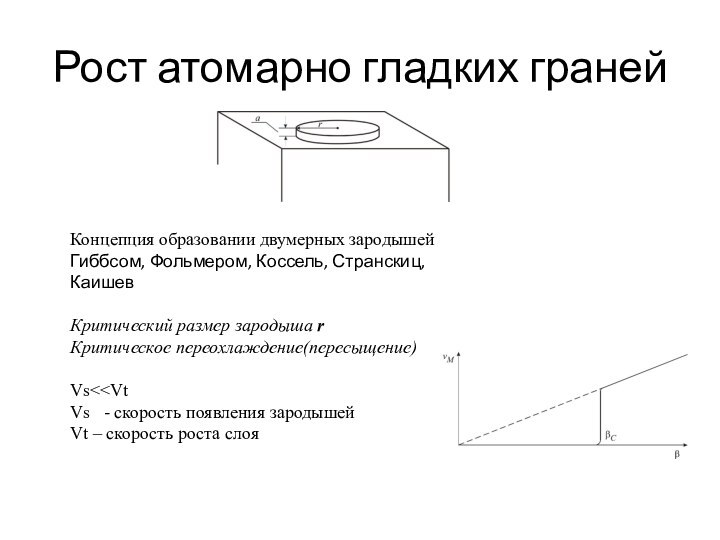
Рост атомарно гладких граней
Концепция образовании двумерных зародышей
Гиббсом, Фольмером,
Коссель, Странскиц, Каишев
Критический размер зародыша r
Критическое переохлаждение(пересыщение) βc
Vs
Vs - скорость появления зародышей
Vt – скорость роста слоя
Слайд 38
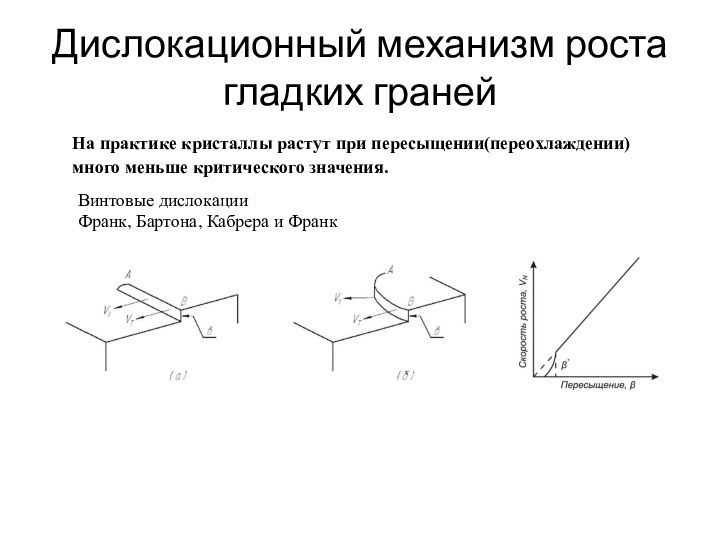
Дислокационный механизм роста гладких граней
Винтовые дислокации
Франк, Бартона,
Кабрера и Франк
На практике кристаллы растут при пересыщении(переохлаждении) много
меньше критического значения.
Слайд 40
Установка «Гранат-2», компоненты теплового узла и
Компоненты теплового
узла: 1 — нагревательный элемент, 2 — блок экранов,
3 — токоввод (левый)Установка «Гранат-2»: 1 — кристаллизационная
камера, 2 — механизм перемещения контейнера
с веществом, 3 — блок управления
Молибденовые трубки
для отжига и роста
Коническая
затравка