Слайд 3
ВВЕДЕНИЕ
Большинство современных конструкционных материалов, в том числе и

композиционных — это кристаллические вещества. Кристалл представляет собой совокупность
правильно расположенных атомов, образующих закономерную структуру, возникшую самопроизвольно из окружающей его неупорядоченной среды.
Причиной, вызывающей симметричное расположение атомов является стремление кристалла к минимуму свободной энергии.
Кристаллизация (возникновение порядка из хаоса, то есть из раствора, пара) происходит с такой же неизбежностью, как, например, процесс падения тел. В свою очередь минимум свободной энергии достигается при наименьшей доле поверхностных атомов в структуре, поэтому внешним проявлением правильного внутреннего атомного строения кристаллических тел является огранение кристаллов.
В 1669 г. датский ученый Н. Стенон обнаружил закон постоянства углов: углы между соответствующими гранями кристалла постоянны и характерны для данного вещества. Любое твердое тело состоит из взаимодействующих частиц. Этими частицами, в зависимости от природы вещества, могут быть отдельные атомы, группы атомов, молекулы, ионы и т.п. Соответственно связь между ними бывает: атомная (ковалентная), молекулярная (связь Ван – дер – Вальса), ионная (полярная) и металлическая.
Слайд 4
В современной кристаллографии можно выделить четыре направления, которые
в известной мере связаны одно с другим:
- геометрическую
кристаллографию, изучающую различные формы кристаллов и законы их симметрии;
- структурную кристаллографию и кристаллохимию, которые изучают пространственное расположение атомов в кристаллах и зависимость его от химического состава и условий образования кристаллов;
- кристаллофизику, изучающую влияние внутреннего строения кристаллов на их физические свойства;
- физико-химическую кристаллографию, которая изучает вопросы образования искусственных кристаллов.
Слайд 5
АНАЛИЗ ПРОСТРАНСТВЕННЫХ РЕШЕТОК
Понятие о пространственной решетке и элементарной
ячейке
При изучении вопроса кристаллического строения тел прежде всего
необходимо иметь четкое представление о терминах: «пространственная решетка» и «элементарная ячейка». Эти понятия используются не только в кристаллографии, но и в целом ряде смежных наук для описания того, как расположены в пространстве материальные частицы в кристаллических телах.
Как известно, в кристаллических телах, в отличие oт аморфных, материальные частицы (атомы, молекулы, ионы) располагаются в определенном порядке, на определенном расстоянии друг от друга.
Слайд 6
Пространственная решетка — это схема, которая показывает расположение
материальных частиц в пространстве. Пространственная решетка (рис.) фактически состоит
из множества одинаковых параллелепипедов, которые целиком, без промежутков, заполняют пространство. Материальные частицы обычно располагаются в узлах решетки — точках пересечения ее ребер.
Пространственная решетка
Слайд 7
Элементарная ячейка — это наименьший параллелепипед, с помощью
которого можно построить всю пространственную решетку путем непрерывных параллельных
переносов (трансляций) в трех направлениях пространства. Вид элементарной ячейки представлен на рис.
Три вектора a, b, c являющиеся ребрами элементарной ячейки, называют векторами трансляции. Их абсолютная величина (a, b, c) — это периоды решетки, или осевые единицы. Вводят в рассмотрение и углы между векторами трансляций — α ( между векторами b, c), β (между a, c) и γ (между a, b). Таким образом, элементарную ячейку определяют шесть величин: три значения периодов (а, в, c ) и три значения углов между ними (α, β, γ ).
Слайд 8
Правила выбора элементарной ячейки
При изучении представлений об элементарной
ячейке следует обратить внимание на то, что величину и
направление трансляций в пространственной решетке можно выбрать по-разному, поэтому форма и размеры элементарной ячейки будут различны.
На рис. рассмотрен двумерный случай. Показана плоская сетка решетки и разные способы выбора плоской элементарной ячейки.
Способы выбора элементарной ячейки
Слайд 9
В середине XIX в. французский кристаллограф О. Браве
предложил следующие условия выбора элементарной ячейки:
1) симметрия элементарной
ячейки должна соответствовать симметрии пространственной решетки;
2) число равных ребер и равных углов между ребрами должно быть максимальным;
3) при наличии прямых углов между ребрами их число должно быть максимальным;
4) при соблюдении этих трех условий объем элементарной ячейки должен быть минимальным.
На основании этих правил Браве доказал, что существует только 14 типов элементарных ячеек, которые получили название трансляционных, поскольку строятся они путем трансляции — переноса. Эти решетки отличаются друг от друга величиной и направлением трансляций, а отсюда вытекает различие в форме элементарной ячейки и в числе узлов с материальными частицами.
Слайд 10
Примитивные и сложные элементарные ячейки
По числу узлов
с материальными частицами элементарные ячейки подразделяется на примитивные и
сложные. В примитивных ячейках Браве материальные частицы находятся только в вершинах, в сложных — в вершинах и дополнительно внутри или на поверхности ячейки.
К числу сложных ячеек относятся объемноцентрированная I , гранецентрированная F и базоцентрированная С. На рис. показаны элементарные ячейки Браве.
Элементарные ячейки Браве: а – примитивная, б – базоцентрированная, в – объемноцентрированная, г – гранецентрированная
Слайд 11
В объемноцентрированной ячейке имеется дополнительный узел в центре

ячейки, принадлежащий только данной ячейке, поэтому здесь имеется два
узла (1/8х8+1 = 2).
В гранецентрированной ячейке узлы с материальными частицами находятся, кроме вершин ячейки, еще в центрах всех шести граней. Такие узлы принадлежат одновременно двум ячейкам: данной и другой, смежной с ней. На долю данной ячейки каждый из таких узлов принадлежит 1/2 часть. Поэтому в гранецентрированной ячейке будет четыре узла (1/8х8+1/2х6 = 4).
Аналогично в базоцентрированной ячейке находятся 2 узла (1/8х8+1/2х2 = 2) с материальными частицами. Основные сведения об элементарных ячейках Браве приведены ниже в табл. 1.1.
Примитивная ячейка Браве содержит трансляции a,b,c только вдоль координатных осей. В объемноцентрированной ячейке добавляется еще трансляция вдоль пространственной диагонали — к узлу, расположенному в центре ячейки. В гранецентрированной, кроме осевых трансляций a,b,c имеются дополнительная трансляция вдоль диагоналей граней, а в базоцентрированной — вдоль диагонали грани, перпендикулярной оси Z.
Слайд 12
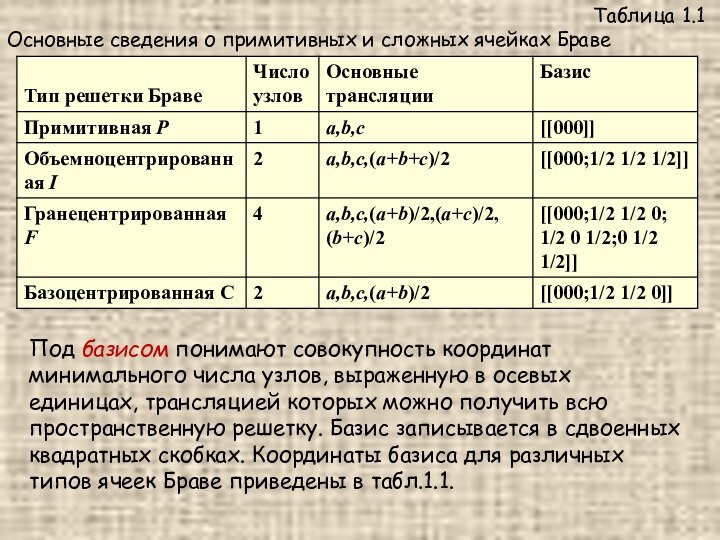
Таблица 1.1
Основные сведения о примитивных и сложных ячейках
Браве
Под базисом понимают совокупность координат минимального числа узлов, выраженную
в осевых единицах, трансляцией которых можно получить всю пространственную решетку. Базис записывается в сдвоенных квадратных скобках. Координаты базиса для различных типов ячеек Браве приведены в табл.1.1.
Слайд 13
Элементарные ячейки Браве
В зависимости от формы все ячейки
Браве распределяются между семью кристаллическими системами (сингониями). Слово «сингонИя»
означает сходноугольность (от греч. σύν - «согласно, вместе, рядом», и γωνία - «угол»). Каждой сингонии соответствуют определенные элементы симметрии. В табл. указаны соотношения между периодами решетки а, в, с и осевыми углами α, β, γ для каждой сингонии
Слайд 14
На рис. представлены все четырнадцать типов элементарных ячеек
Браве, распределенные по сингониям. Гексагональная ячейка Браве представляет собой
базоцентрированную шестигранную призму. Однако очень часто ее изображают иначе — в виде четырехгранной призмы с ромбом в основании, которая представляет одну из трех призм, составляющих шестигранную (на рис. она представлена сплошными линиями). Такое изображение проще и удобнее, хотя связано с нарушением принципа соответствия симметрии (первый принцип выбора элементарной ячейки по Браве).
Слайд 15
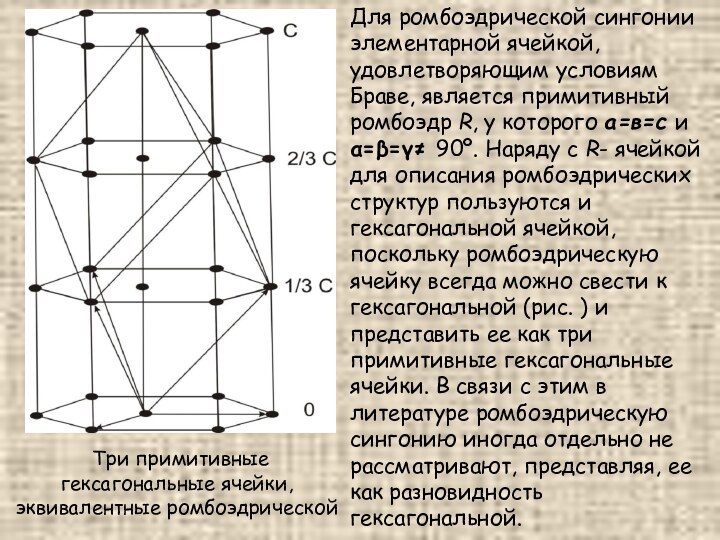
Для ромбоэдрической сингонии элементарной ячейкой, удовлетворяющим условиям Браве,
является примитивный ромбоэдр R, у которого а=в=с и α=β=γ≠
90º. Наряду с R- ячейкой для описания ромбоэдрических структур пользуются и гексагональной ячейкой, поскольку ромбоэдрическую ячейку всегда можно свести к гексагональной (рис. ) и представить ее как три примитивные гексагональные ячейки. В связи с этим в литературе ромбоэдрическую сингонию иногда отдельно не рассматривают, представляя, ее как разновидность гексагональной.
Три примитивные гексагональные ячейки, эквивалентные ромбоэдрической
Слайд 16
Понятие о координационном числе
В сложных ячейках материальные
частицы уложены более плотно, чем в примитивных, более полно
заполняют объем ячейки, больше связаны друг с другом. Для характеристики этого вводят понятие о координационном числе.
Под координационным числом данного атома понимают число ближайших соседних атомов. Если речь идет о координационном числе иона, то подразумевается число ближайших к нему ионов противоположного знака. Чем больше координационное число, тем с большим числом атомов или ионов связан данный, тем больше места занято частицами, тем компактнее решетка.
Принято сингонии с одинаковыми соотношениями между осевыми единицами объединять в одну категории. Поэтому триклинную, моноклинную и ромбическую сингонии объединяют в низшую категорию (а≠в≠с), тетрагональную, гексагональную (и производную от нее ромбоэдрическую) – в среднюю (а=в≠с), к высшей категории (а=в=с) относится кубическая сингония.
Слайд 17
Пространственные решетки металлов
Наиболее распространенные среди металлов пространственные

решетки относительно просты. Они большей частью совпадают с трансляционными
решетками Браве: кубической объемноцентрированной и гранецентрированной. В узлах этих решеток располагаются атомы металлов. В решетке объемноцентрированного куба (ОЦК - решетки) каждый атом окружен восемью ближайшими соседями, и координационное число КЧ = 8. Решетку ОЦК имеют металлы: α-Fe, Li, Na, K, V, Cr, Ta, W, Mo, Nb и др.
В решетке гранецентрированного куба (ГЦК - решетки) КЧ = 12: любой атом, расположенный в вершине ячейки имеет двенадцать ближайших соседей, которыми является атомы, находящиеся в центрах граней. Решетку ГЦК имеют металлы: Al, Ni, Cu, Pd, Ag, Ir, Pt, Pb и др.
Наряду с этими двумя, среди металлов (Be, Mg, Sc, α-Ti, α-Co, Zn, Y, Zr, Re, Os, Tl, Cd и др.) встречается еще гексагональная компактная. Эта решетка не является трансляционной решеткой Браве, так как простыми трансляциями ее нельзя описать.
Слайд 18
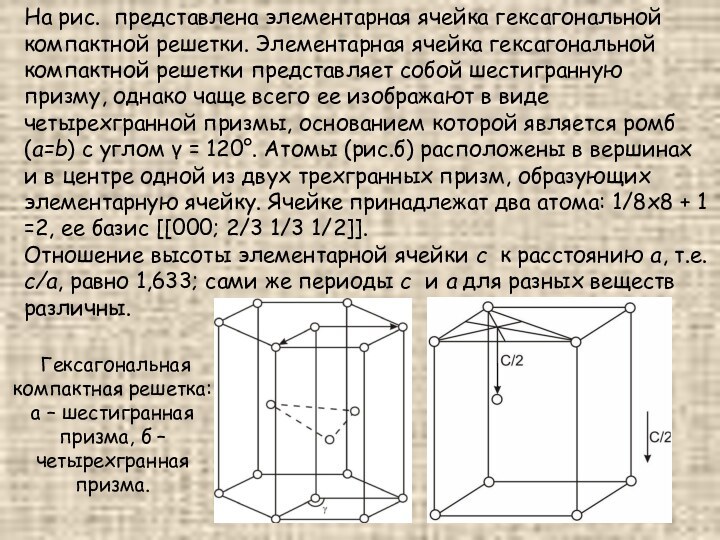
На рис. представлена элементарная ячейка гексагональной компактной решетки.
Элементарная ячейка гексагональной компактной решетки представляет собой шестигранную призму,
однако чаще всего ее изображают в виде четырехгранной призмы, основанием которой является ромб (a=b) c углом γ = 120°. Атомы (рис.б) расположены в вершинах и в центре одной из двух трехгранных призм, образующих элементарную ячейку. Ячейке принадлежат два атома: 1/8х8 + 1 =2, ее базис [[000; 2/3 1/3 1/2]].
Отношение высоты элементарной ячейки c к расстоянию a, т.е. c/a, равно 1,633; сами же периоды c и a для разных веществ различны.
Гексагональная компактная решетка: а – шестигранная призма, б – четырехгранная призма.
Слайд 19
КРИСТАЛЛОГРАФИЧЕСКИЕ ИНДЕКСЫ
Кристаллографические индексы плоскости
В
кристаллографии часто приходится описывать взаимное расположение отдельных плоскостей кристалла,
его направлений, для чего удобно пользоваться кристаллографическими индексами. Кристаллографические индексы дают представление о расположении плоскости или направления относительно системы координат. При этом не имеет значения, прямоугольная или косоугольная система координат, одинаковые или разные масштабные отрезки по координатным осям. Представим себе ряд параллельных плоскостей, проходящих через одинаковые узлы пространственной решетки. Эти плоскости расположены на одинаковом расстоянии друг от друга и составляют семейство параллельных плоскостей. Они одинаково ориентированы в пространстве и потому характеризуются одинаковыми индексами.
Слайд 20
Выберем из этого семейства какую-либо плоскость и введем
в рассмотрение отрезки, которые плоскость отсекает по координатным осям
(координатные оси x, y, z обычно совмещают с ребрами элементарной ячейки, масштаб по каждой оси равняется соответствующей осевой единице — периоду a, или b, или c). Величины отрезков выражают в осевых единицах.
Кристаллографические индексы плоскости (индексы Миллера) — это три наименьших целых числа, которые обратно пропорциональны числу осевых единиц, отсекаемых плоскостью на координатных осях.
Индексы плоскости обозначаются буквами h, k, l, записываются подряд и заключаются в круглые скобки—(hkl).
Слайд 21
Индексами (hkl) характеризуются все плоскости семейства параллельных плоскостей.
Этот символ означает, что семейство параллельных плоскостей рассекает осевую
единицу вдоль оси x на h частей, вдоль оси y на k частей и вдоль оси z на l частей.
При этом плоскость ближайшая к началу координат, отсекает на координатных осях отрезки 1/h (по оси x), 1/k (по оси y), 1/l (по оси z).
Порядок нахождения кристаллографических индексов плоскости.
Находим отрезки, отсекаемые плоскостью на координатных осях, измеряя их в осевых единицах.
2. Берем обратные значения этих величин.
3. Приводим отношение полученных чисел к отношению трех наименьших целых чисел.
4. Полученные три числа заключаем в круглые скобки.
Слайд 22
Пример. Найти индексы плоскости, которая отсекает на координатных
осях следующие отрезки: 1/2; 1/4; 1/4. Поскольку длины отрезков
выражены в осевых единицах, имеем 1/h=1/2; 1/k=1/4; 1/l=1/4.
Находим обратные значения и берем их отношение
h : k : l = 2 : 4 : 4.
Сократив на два, приведем отношение полученных величин к отношению трех целых наименьших чисел: h : k : l = 1 : 2 : 2. Индексы плоскости записываем в круглых скобках подряд, без запятых — (122). Они читаются порознь — "один, два, два".
Если плоскость пересекает кристаллографическую ось в отрицательном направлении, над соответствующим индексом сверху ставится знак "минус". Если плоскость параллельна какой-либо координатной оси, то в символе плоскости индекс, соответствующий этой оси, равен нулю. Например, символ (hko) означает, что плоскость пересекается с осью z в бесконечности и индекс плоскости по этой оси будет 1/∞ = 0.
Слайд 23
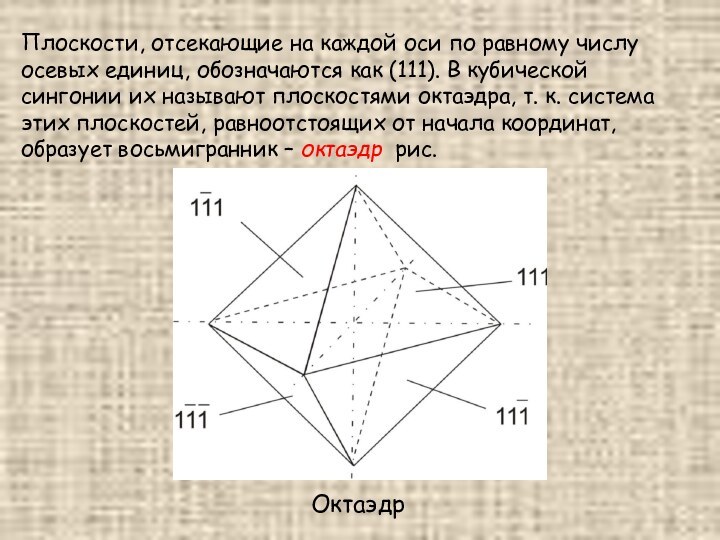
Плоскости, отсекающие на каждой оси по равному числу
осевых единиц, обозначаются как (111). В кубической сингонии их
называют плоскостями октаэдра, т. к. система этих плоскостей, равноотстоящих от начала координат, образует восьмигранник – октаэдр рис.
Октаэдр
Слайд 24
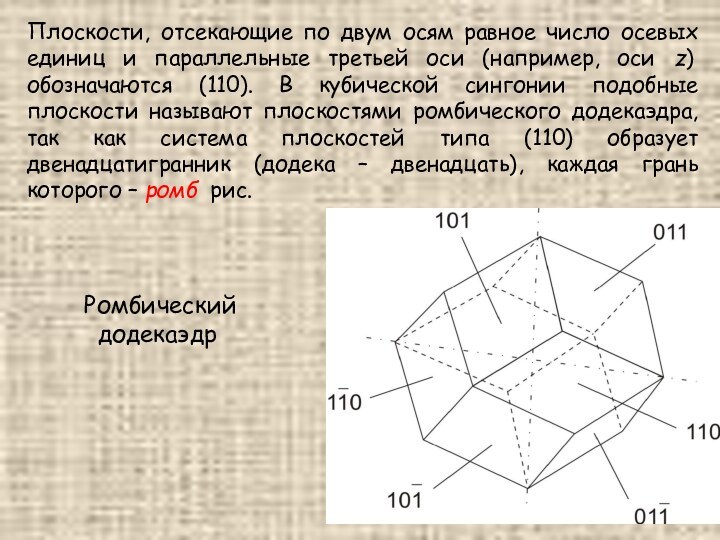
Плоскости, отсекающие по двум осям равное число осевых
единиц и параллельные третьей оси (например, оси z) обозначаются
(110). В кубической сингонии подобные плоскости называют плоскостями ромбического додекаэдра, так как система плоскостей типа (110) образует двенадцатигранник (додека – двенадцать), каждая грань которого – ромб рис.
Ромбический додекаэдр
Слайд 25
Плоскости, пересекающие одну ось и параллельные двум другим
(например, осям y и z), обозначают — (100) и
называют в кубической сингонии плоскостями куба, то есть система подобных плоскостей образует куб.
При решений различных задач, связанных с построением в элементарной ячейке плоскостей, систему координат целесообразно выбрать так, чтобы искомая плоскость располагалась в заданной элементарной ячейке. Например, при построении плоскости (211) в кубической ячейке начало координат удобно перенести из узла О в узел О’ .
Плоскость куба (211 )
Слайд 27
Иногда индексы плоскости записывают в фигурных скобках {hkl}.Эта
запись означает символ совокупности идентичных плоскостей. Такие плоскости проходят
через одинаковые узлы в пространственной решетке, симметрично расположены в пространстве и характеризуются одинаковым межплоскостным расстоянием.
Плоскости октаэдра в кубической сингонии принадлежат к одной совокупности {111}, они представляют грани октаэдра и имеют следующие индексы: {111} →(111), (111), (111), (111), (111), (111), (111 ), (111 ).
Символы всех плоскостей совокупности находят путем перестановки местами и изменения знаков отдельных индексов.
Для плоскостей ромбического додекаэдра обозначение совокупности: {110} → (110), (110), (110),
(110), (101), (101), (101), (101), (011), (011), (011), (011).
Слайд 30
КРИСТАЛЛОГРАФИЧЕСКИЕ ИНДЕКСЫ УЗЛА
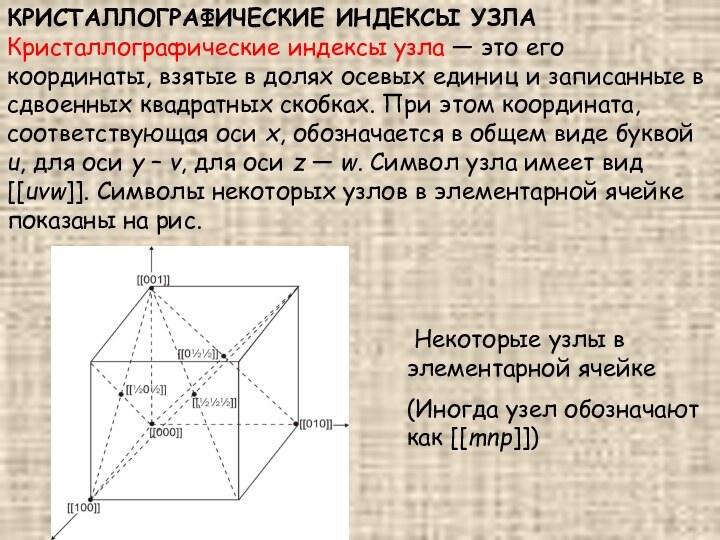
Кристаллографические индексы узла — это
его координаты, взятые в долях осевых единиц и записанные
в сдвоенных квадратных скобках. При этом координата, соответствующая оси x, обозначается в общем виде буквой u, для оси y – v, для оси z — w. Символ узла имеет вид [[uvw]]. Символы некоторых узлов в элементарной ячейке показаны на рис.
Некоторые узлы в элементарной ячейке
(Иногда узел обозначают как [[mnp]])
Слайд 31
Кристаллографические индексы направления
В кристалле, где все
параллельные направления идентичны друг другу, направление, проходящее через начало
координат, характеризует все данное семейство параллельных направлений.
Положение в пространстве направления, проходящего через начало координат, определяется координатами любого узла, лежащего на этом направлении.
Координаты любого узла, принадлежащего направлению, выраженные в долях осевых единиц и приведенные к отношению трех целых наименьших чисел, и есть кристаллографические индексы направления. Они обозначаются целыми числам u, v, w и записываются слитно в квадратных скобках [uvw].
Слайд 32
Порядок нахождения индексов направления
1. Из семейства
параллельных направлений выбрать такое, которое проходит через начало координат,
или перенести данное направление параллельно самому себе в начало координат, или перенести начало координат в узел, лежащий на данном направлении.
2. Найти координаты любого узла, принадлежащего данному направлению, выразив их в осевых единицах.
3. Взять отношение координат узла и привести его к отношению трех целых наименьших чисел.
4. Полученные три числа заключить в квадратные скобки.
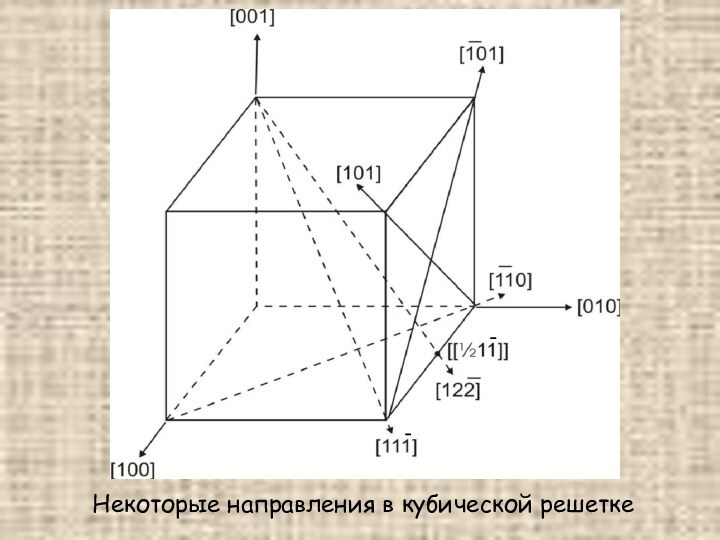
Важнейшие направления в кубической решетке и их индексы представлены на рис.
Слайд 33
Некоторые направления в кубической решетке
Слайд 34
ПОНЯТИЕ О КРИСТАЛЛИЧЕСКОМ И ПОЛЯРНОМ КОМПЛЕКСЕ
Метод кристаллографических
проекций основан на одной из характерных особенностей кристаллов —
законе постоянства углов: углы между определенными гранями и ребрами кристалла всегда постоянны.
Так, когда кристалл растет, меняются размеры граней, их форма, но углы остаются неизменными. Поэтому в кристалле можно перенести все ребра и грани параллельно самим себе в одну точку пространства; угловые соотношения при этом сохраняется.
Такая совокупность плоскостей и направлений, параллельных плоскостям и направлениям в кристалле и проходящая через одну точку, получила название кристаллического комплекса, а сама точка называется центром комплекса. При построении кристаллографических проекций кристалл всегда заменяют кристаллическим комплексом.
Слайд 35
Чаще рассматривают не кристаллический комплекс, а полярный (обратный).
Полярный комплекс, получают из кристаллического (прямого) путем замены плоскостей
нормалями к ним, а направлений - перпендикулярными к ним плоскостями.
а б в
Куб (а), его кристаллический (б) и
полярный комплекс (в)
Слайд 36
СИММЕТРИЯ КРИСТАЛЛИЧЕСКИХ МНОГОГРАННИКОВ (СИММЕТРИЯ КОНТИНУУМА)
ПОНЯТИЕ О
СИММЕТРИИ
Кристаллы существуют в природе в виде кристаллических многогранников.
Кристаллы разных веществ отличаются друг от друга по своим формам. Каменная соль — это кубики; горный хрусталь — шестигранные призмы, заостренные на концах; алмаз — чаще всего правильные восьмигранники (октаэдры); кристаллы граната — двенадцатигранники (рис. ).
Такие кристаллы обладают симметрией.
Слайд 37
Характерной особенностью кристаллов является анизотропия их свойств: в
различных направлениях они разные, но в параллельных направлениях одинаковы,
а также одинаковы и в симметричных направлениях.
Не всегда кристаллы имеют форму правильных многогранников. В реальных условиях роста, при затруднении в свободном росте симметричные грани могут развиваться неравномерно и правильная внешняя форма может не получиться, однако правильное внутреннее строение при этом полностью сохраняется, а также сохраняется симметрия физических свойств.
Греческое слово "симметрия" означает соразмерность. Симметричная фигура состоит из равных, одинаковых частей. Под симметрией понимают свойство тел или геометрических фигур совмещать отдельные части друг с другом при некоторых симметрических преобразованиях. Геометрические образы, с помощью которых задаются и осуществляются симметрические преобразования, называют элементами симметрии.
Слайд 38
Рассматривая симметрию внешней огранки кристалла, кристаллическую среду представляют
себе как непрерывную, сплошную, так называемый континуум (в переводе
с латинского на русский - означает непрерывный, сплошной). Все точки такой среде совершенно одинаковы.
Элементы симметрии континуума описывают внешнюю форму кристаллического многогранника, поэтому их еще называют макроскопическими элементами симметрии.
Фактически же кристаллическая среда является дискретной. Кристаллы состоят из отдельных частиц (атомов, ионов, молекул), которые расположены в пространстве в виде бесконечно простирающихся пространственных решеток. Симметрия в расположении этих частиц сложнее и богаче, чем симметрия внешних форм кристаллических многогранников. Поэтому наряду с континуумом рассматривается и дисконтинуум — дискретная, реальная структура материальных частиц со своими элементами симметрии, получившими название микроскопических элементов симметрии.
Слайд 39
Элементы симметрии
В кристаллических многогранниках встречаются простые элементы
симметрии (центр симметрии, плоскость симметрии, поворотная ось) и сложный
элемент симметрии (инверсионная ось).
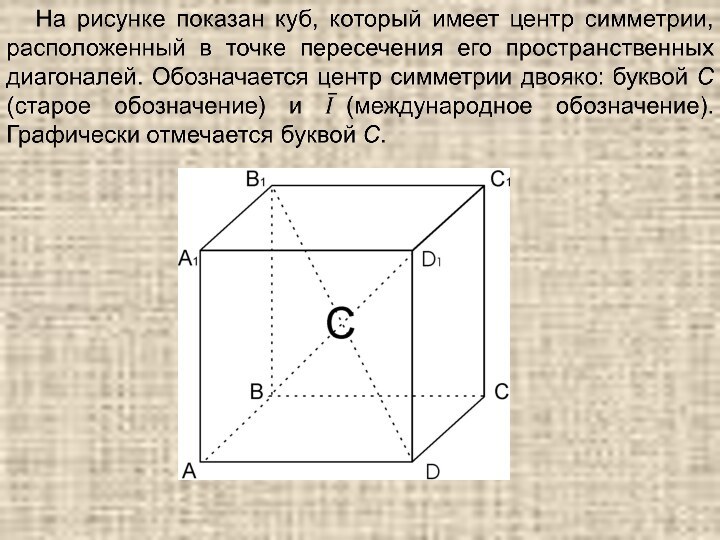
Центр симметрии (или центр инверсии) — особая точка внутри фигуры, при отражении в которой любая точка фигуры имеет эквивалентную себе, то есть обе точки (например, пара вершин) расположены на одной прямой, проходящей через центр симметрии, и равноудалены от него. При наличии центра симметрии каждая грань пространственной фигуры имеет параллельную и противоположно направленную грань, каждому ребру соответствует равноудаленное, равное, параллельное, но противоположно направленное ребро. Поэтому центр симметрии представляет собой как бы зеркальную точку.
Слайд 41
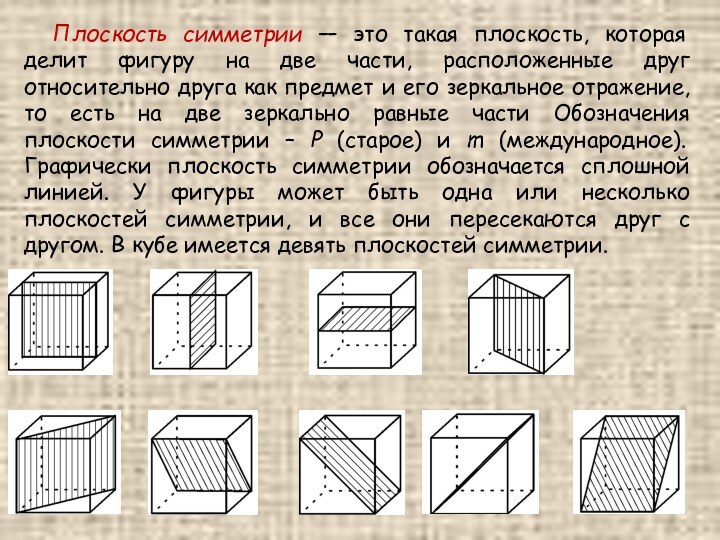
Плоскость симметрии — это такая плоскость, которая делит
фигуру на две части, расположенные друг относительно друга как
предмет и его зеркальное отражение, то есть на две зеркально равные части Обозначения плоскости симметрии – Р (старое) и m (международное). Графически плоскость симметрии обозначается сплошной линией. У фигуры может быть одна или несколько плоскостей симметрии, и все они пересекаются друг с другом. В кубе имеется девять плоскостей симметрии.
Слайд 42
Поворотная ось — это такая прямая, при повороте
вокруг которой на некоторый определенный угол α фигура совмещается
сама с собой. Величина угла поворота α определяет порядок поворотной оси n, который показывает, сколько раз фигура совместится сама с собой при полном обороте вокруг этой оси (на 360°):
В изолированных геометрических фигурах возможны оси симметрии любых порядков, но в кристаллических многогранниках порядок оси ограничен, он может иметь только следующие значения: n= 1, 2, 3, 4, 6. В кристаллических многогранниках невозможны оси симметрии пятого и выше шестого порядков. Это вытекает из принципа непрерывности кристаллической среды. Обозначения осей симметрии: старые - Ln (L1, L2, L3, L4, L6) и международные - арабскими цифрами, соответствующими порядку поворотной оси (1, 2, 3, 4, 6).
Слайд 43
Графически поворотные оси изображаются многоугольниками:
Слайд 45
Понятие о классе симметрии
Каждый кристаллический многогранник обладает
набором элементов симметрии. Сочетаясь друг с другом, элементы симметрии
кристалла обязательно пересекаются, и при этом возможно появление новых элементов симметрии.
В кристаллографии доказываются следующие теоремы сложения элементов симметрии:
Линия пересечения двух плоскостей симметрии есть ось симметрии, для которой угол поворота вдвое больше угла между плоскостями.
Через точку пересечения двух осей симметрии проходит третья ось симметрии.
В точке пересечения плоскости симметрии с перпендикулярной к ней осью симметрии четного порядка возникает центр симметрии.
Число осей второго порядка, перпендикулярных главной оси симметрии высшего порядка (третьего, четвертого, шестого), равно порядку главной оси.
Слайд 46
5. Число плоскостей симметрии, пересекающихся по главной оси
высшего порядка, равно порядку этой оси.
Число сочетаний элементов
симметрии друг с другом в кристаллах строго ограничено. Все возможные сочетания элементов симметрии в кристаллах выводятся строго математически, принимая во внимание теоремы сложения элементов симметрии.
Полный набор элементов симметрии, присущих данному кристаллу, называется его классом симметрии. Строгий математический вывод показывает, что все возможные для кристаллических многогранников сочетания элементов симметрии исчерпываются тридцатью двумя классами симметрии.
Слайд 48
Связь между пространственной решеткой и элементами симметрии
Наличие
тех или иных элементов симметрии определяет геометрию пространственной решетки,
накладывая определенные условия на взаимное расположение координатных осей и равенство осевых единиц.
Существуют общие правила выбора координатных осей, учитывающие набор элементов симметрии кристалла.
Координатные оси совмещают с особыми или единичными направлениями, неповторяющимися в кристалле - поворотными или инверсионными осями, для которых порядок оси больше единицы, и нормалями к плоскости симметрии.
Если в кристалле только одно особое направление, с ним совмещают одну из координатных осей, обычно ось Z. Две другие оси располагают в плоскости, перпендикулярной особому направлению параллельно ребрам кристалла.
При отсутствии особых направлений координатные оси выбирают параллельно трем не лежащим в одной плоскости ребрам кристалла.
Слайд 49
Исходя из этих правил, можно получить все
семь кристаллических систем, или сингоний. Они отличаются друг от
друга соотношением масштабных единиц а, b, c и осевыми углами α, β, γ. Три возможности: а≠b≠c, а=b≠c, а=b=c позволяют распределить все кристаллографические координатные системы (сингонии) по трем категориям - низшей, средней и высшей.
Каждая категория характеризуется наличием определенных элементов симметрии. Так, у кристаллов низшей категории нет осей высшего порядка, то есть осей 3, 4 и 6, а могут быть оси второго порядка, плоскости и центр симметрии.
У кристаллов средней категории имеется ось высшего порядка, а также могут быть оси второго порядка, плоскости симметрии, центр симметрии.
Самые симметричные кристаллы относятся к высшей категории. У них имеется несколько осей высшего порядка (третьего и четвертого), могут быть оси второго порядка, плоскости и центр симметрии. Однако отсутствуют оси шестого порядка.
Слайд 51
Понятие о симметрии дисконтинуума и пространственной группе
Наличие
32 классов симметрии кристаллических многогранников показывает, что все многообразие
внешних форм кристалла подчиняется законам симметрии.
Симметрия внутренней структуру кристаллов, расположения частиц (атомов, ионов, молекул) внутри кристаллов должна быть сложнее, поскольку внешняя форма кристаллов ограничена, а кристаллическая решетка простирается бесконечно во все стороны пространства.
Законы расположения частиц в кристаллах были установлены великим русским кристаллографом Е. С. Федоровым в 1891 г. Им было найдено 230 способов расположения частиц в пространственной решетке — 230 пространственных групп симметрии.
Слайд 52
Элементы симметрии пространственных решеток
Помимо описанных выше элементов
симметрии (центр симметрии, плоскость симметрии, поворотные и инверсионные оси),
в дискретной среде возможны и другие элементы симметрии, связанные с бесконечностью пространственной решетки и периодической повторяемостью в расположении частиц.
Рассмотрим новые виды симметрии, присущие только дисконтинууму. Их три: трансляция, плоскость скользящего отражения и винтовая ось.
Трансляция — это перенос всех частиц по параллельным направлениям в одну и ту же сторону на одинаковую величину.
Трансляция является простым элементом симметрии, присущим каждой пространственной решетке.
Слайд 53
Комбинация трансляции с плоскостью симметрии приводит к появлению
плоскости скользящего отражения, сочетание трансляции с поворотной осью создает
винтовую ось.
Плоскость скользящего отражения, или плоскость скольжения — это такая плоскость, при отражении в которой как в зеркале с последующей трансляцией вдоль направления, лежащего в данной плоскости, на величину, равную половине периода идентичности для данного направления, совмещаются все точки тела. Под периодом идентичности, как и ранее, будем понимать расстояние между точками вдоль какого-то направления (например, периоды а, b, с в элементарной ячейке — это периоды идентичности вдоль координатных осей X, Y, Z).
Слайд 54
Винтовая ось — это прямая, поворот вокруг которой
на некоторый угол, соответствующий порядку оси, с последующей трансляцией
вдоль оси на величину, кратную периоду идентичности t, совмещает точки тела.
Обозначение винтовой оси в общем виде nS ,где n характеризует порядок поворотной оси (n=1, 2, 3, 4, 6), а St/n- величину трансляции вдоль оси. При этом SОбозначение винтовой оси второго порядка будет 21. Совмещение частиц произойдет после поворота вокруг оси на 180° с последующей трансляцией вдоль направления, параллельного оси, на t/2.
Обозначение винтовой оси третьего порядка будет 31. Однако возможны оси с переносом, кратным наименьшему. Поэтому возможна винтовая ось 32 с трансляцией 2t/3.
Слайд 55
Оси 31 и 32 означают поворот вокруг оси
на 120° по часовой стрелке с последующим переносом. Эти
винтовые оси называются правыми. Если же поворот производить против часовой стрелки, то центровые оси симметрии называются левыми. При этом действие оси 31 правой тождественно действию оси 32 левой и 32 правой — 31 левой.
Так же могут рассматриваться винтовые оси симметрии четвертого и шестого порядков: оси 41 и 43 оси 61 и 65, 62 и 64. могут быть правам и левыми. Действие осей 21, 42 и 63 не зависит от выбора направления вращения вокруг оси. Поэтому они являются нейтральными. Условные обозначения винтовых осей симметрии:
Слайд 57
Обозначение пространственной группы симметрии
Символ пространственной группы содержит
полную информацию о симметрии кристаллической структуры. На первом месте
в символе пространственной группы ставится буква, характеризующая тип решетки Браве: Р - примитивная, С - базоцентрированная, I - обьемноцентрированная, F - гранецентрированная. В ромбоэдрической сингонии на первом месте ставят букву R.
Далее следуют одно, два или три числа или буквы, указывающие элементы симметрии в главных направлениях, аналогично тому, как это делается при составлении обозначения класса симметрии.
Если в структуре в каком-нибудь из главных направлений одновременно располагаются и плоскости симметрии и оси симметрии, предпочтение отдается плоскостям симметрии, и в символ пространственной группы записываются плоскости симметрии.
Слайд 58
При наличии нескольких осей предпочтение отдается простым осям
— поворотным и инверсионным, поскольку их симметрия является более
высокой, чем симметрия винтовых осей.
Имея символ пространственной группы, легко можно определить тип решетки Браве, сингонию ячейки, элементы симметрии в главных направлениях. Так, пространственная группа P42/mnm ( Федоровские группы дитетрагонально-дипирамидального вида симметрии, 135 группа) характеризует примитивную ячейку Браве в тетрагональной сингонии (винтовая ось четвертого порядка 42 определяет тетрагональную сингонию).
В главных направлениях расположены следующие элементы симметрии. С направлением [001] — оси Z совпадает винтовая ось 42 ,которая перпендикулярна симметрии m. В направлениях [100] и [010] (оси Х и Y) расположена плоскость скользящего отражения типа n, в направлении [110] проходит плоскость симметрии m.
Слайд 59
Дефекты в строении кристаллических тел
Дефекты тел делят на
динамические (временные) и статические (постоянные).
1. Динамические дефекты возникают при
механических, тепловых, электромагнитных воздействиях на кристалл.
К ним относятся фононы – временные искажения регулярности решетки, вызванные тепловым движением атомов.
2. Статические дефекты
Различают точечные и протяженные несовершенства структуры тел.
Слайд 60
Точечные дефекты: незанятые узлы решетки (вакансии); смещения
атома из узла в междоузлие; внедрения в решетку чужеродного
атома или иона.
Протяженные дефекты: дислокации (краевая и винтовая), поры, трещины, границы зерен, микровключения другой фазы. Часть дефектов показана на рисунке.
Слайд 62
К основным свойствам относятся: механические, тепловые, электрические, магнитные
и технологические, а также их сопротивление коррозии.
Механические свойства материалов
характеризуют возможность их использования в изделиях, эксплуатируемых при воздействии механи-ческих нагрузок. Основными показателями таких свойств служат параметры прочности и твердость. Они зависят не только от природы мате-риалов, но и от формы, размеров и состояния поверхности образцов, а также режимов испытаний, прежде всего, от скорости нагружения, температуры, воздействия сред и других факторов.
Прочность – свойство материалов сопротивляться разрушению, а также необратимому изменению формы образца под действием внешних нагрузок.
Предел прочности – напряжение, соответствующее максимальному (в момент разрушения образца) значению нагрузки. Отношение наибольшей силы, действующей на образец, к исходной площади его поперечного сечения называют разрушающим напряжением и обозначают σв.
Слайд 63
Деформирование – изменение относительного расположения частиц в материале.

Наиболее простые его виды – растяжение, сжатие, изгиб, кручение,
сдвиг. Деформация – изменение формы и размеров образца в результате деформирования.
Параметры деформирования – относительное удлинение ε = (l– l0)/l0 (где l0 и l – длина образца исходная и после деформирования), угол сдвига – изменение прямого угла между лучами, исходящими из одной точки в образце, при его деформировании. Деформацию называют упругой, если она исчезает после снятия нагрузки, или пластической, если она не исчезает (необратима). Пластическими свойствами материалов при малых деформациях часто пренебрегают.
Предел упругости – напряжение, при котором остаточные деформации (т. е. деформации, обнаруживаемые при разгрузке образца) достигают значения, установленного техническими условиями. Обычно допуск на остаточную деформацию составляет 10–3 ÷10–2 %. Предел упругости σу ограничивает область упругих деформаций материала.
Понятие о модуле как о характеристике упругости материалов возникло при рассмотрении идеально упругих тел, деформация которых линейно зависит от напряжения. При простом растяжении (сжатии)
σ = Еε
где Е – модуль Юнга, или модуль продольной упругости, который характеризует сопротивление материалов упругой деформации (растя-жению, сжатию); ε − относительная деформация.
Слайд 64
При сдвиге в материале по направлению сдвига и
по нормали к нему действуют только касательные напряжения
где G
– модуль сдвига, характеризующий упругость материала при изменении формы образца, объем которого остается постоянным; γ − угол сдвига.
При всестороннем сжатии в материале по всем направлениям действует нормальное напряжение
где К − модуль объемной упругости, который характеризует сопротивление материала изменению объема образца, не сопровождающемуся изменением его формы; ∆ – относительное объемное сжатие.
Постоянной величиной, характеризующей упругость материалов при одноосном растяжении, является коэффициент Пуассона:
где ε′ – относительное поперечное сжатие; ε – относительное продольное удлинение образца.
Слайд 65
Твердость является механической характеристикой материалов, комплексно отражающей их
прочность, пластичность, а также свойства поверхностного слоя образцов. Она
выражается сопротивлением материала местному пластическому деформированию, возникающему при внедрении в образец более твердого тела – индентора. Вдавливание индентора в образец с последующим измерением размеров отпечатка является основным технологическим приемом при оценке твердости материалов. В зависимости от особенностей приложения нагрузки, конструкции инденторов и определения чисел твердости различают методы Бринелля, Роквелла, Виккерса, Шора. При измерении микротвердости по ГОСТ 9450–76 на поверхности образца остаются отпечатки незначительной глубины, поэтому такой метод используют, когда образцы выполнены в виде фольги, пленок, покрытий малой толщины. Метод определения пластической твердости заключается во вдавливании в образец сферического наконечника путем последовательного приложения различных нагрузок.
Слайд 66
Коррозия – физико-химический процесс изменения свойств, повреждения структуры

и разрушения материалов вследствие перехода их компонентов в химические
соединения с компонентами окружающей среды. Под коррозионным повреждением понимают любой дефект структуры материала, возникший в результате коррозии. Если механические воздействия ускоряют коррозию материалов, а коррозия облегчает их механическое разрушение, имеет место коррозионно-механическое повреждение материалов. Потери материалов из-за коррозии и затраты на защиту от нее машин и оборудования непрерывно увеличиваются вследствие активизации производственной деятельности человека и загрязнения окружающей среды отходами производства.
Наиболее часто сопротивление материалов коррозии характеризуют с помощью параметра коррозионной стойкости – величины, обратной технической скорости коррозии материала в данной коррозионной системе. Условность этой характеристики заключается в том, что она относится не к материалу, а к коррозионной системе. Коррозионную стойкость материала нельзя изменить, не изменив других параметров коррозионной системы. Противокоррозионная защита – это модифицирование коррозионной системы, ведущее к снижению скорости коррозии материала.
Слайд 67
Температурные характеристики.
Жаростойкость – свойство материалов сохранять или незначительно

изменять механические параметры при высоких температурах. Свойство металлов противостоять
коррозионному воздействию газов при высоких температурах называют жароупорностью. В качестве характеристики жаростойкости легкоплавких материалов используют температуру размягчения.
Жаропрочность – свойство материалов длительное время сопротивляться деформированию и разрушению при высоких температурах. Это важнейшая характеристика материалов, эксплуатируемых при температурах Т > 0,3 Тпл. Такие условия имеют место в двигателях внутреннего сгорания, паросиловых установках, газовых турбинах, металлургических печах и др.
При низких температурах (в технике – от 0 до –269 °С) увеличивается статическая и циклическая прочность материалов, снижаются их пластичность и вязкость, повышается склонность к хрупкому разрушению.
Хладноломкость – возрастание хрупкости материалов при понижении температуры. Склонность материала к хрупкому разрушению определяют по результатам ударных испытаний образцов с надрезом при понижении температуры.
Слайд 68
Тепловое расширение материалов регистрируют по изменению размеров и

формы образцов при изменении температуры. У газов оно обусловлено
увеличением кинетической энергии частиц при нагревании, у жидкостей и твердых материалов связано с несимметричностью тепловых колебаний атомов, благодаря чему межатомные расстояния с ростом температуры увеличиваются.
Количественно тепловое расширение материалов характеризуют температурным коэффициентом объемного расширения:
а твердых материалов – и температурным коэффициентом линейного расширения (ТКЛР):
– изменения линейного размера, объема образцов и температуры (соответственно).
Индекс ξ служит для обозначения условий теплового расширения (обычно – при постоянном давлении).
Экспериментально αV и αl определяют методами дилатометрии, изучающей зависимость изменения размеров тел при воздействии внешних факторов. Специальные измерительные приборы – дилатометры – различаются устройством датчиков и чувствительностью систем регистрации размеров образцов.
Слайд 69
Теплоемкость – отношение количества теплоты, полученной телом при

бесконечно малом изменении его состояния в каком-либо процессе, к
вызванному последним приращению температуры:
По признакам термодинамического процесса, в котором определяют теплоемкость материала, различают теплоемкость при постоянном объеме и при постоянном давлении. В процессе нагревания при постоянном давлении (изобарный процесс) часть теплоты расходуется на расширение образца, а часть – на увеличение внутренней энергии материала. Теплота, сообщенная тому же образцу при постоянном объеме (изохорный процесс), расходуется только на увеличение внутренней энергии материала.
Удельная теплоемкость, Дж/(кг·К)], – отношение теплоемкости к массе тела. Различают удельную теплоемкость при постоянном давлении (ср) и при постоянном объеме (сv). Отношение теплоемкости к количеству вещества называют молярной теплоемкостью (сm), Дж/(моль⋅К). Для всех веществ ср > сv, для разреженных (близких к идеальным) газов сmp – сmv = R (где R = 8,314 Дж/(моль⋅К) – универсальная газовая постоянная).
Слайд 70
Теплопроводность – перенос энергии от более нагретых участков
тела к менее нагретым в результате теплового движения и
взаимодействия микрочастиц. Эта величина характеризует самопроизвольное выравнивание температуры твердых тел.
Для изотропных материалов справедлив закон Фурье, согласно которому вектор плотности теплового потока q пропорционален и противоположен по направлению градиенту температуры Т:
где λ – коэффициент теплопроводности [Вт/(м·К)], зависящий от агрегатного состояния, атомно-молекулярного строения, структуры, температуры и других параметров материала.
Коэффициент температуропроводности (м2/с) является мерой теплоизоляционных свойств материала:
где ρ – плотность; ср – удельная теплоемкость материала при
постоянном давлении.
Слайд 71
Технологические свойства материалов характеризуют податливость материалов технологическим воздействиям

при переработке в изделия. Знание этих свойств позволяет обоснованно
и рационально проектировать и осуществлять технологические процессы изготовления изделий. Основными технологическими характеристиками материалов являются обрабатываемость резанием и давлением, литейные параметры, свариваемость, склонность к деформации и короблению при тепловой обработке и др.
Обрабатываемость резанием характеризуют следующими показателями: качеством обработки материалов − шероховатостью обработанной поверхности и точностью размеров образца, стойкостью инструмента, сопротивлением резанию − скоростью и силой резания, видом стружко-образования. Значения показателей определяют при обтачивании образцов и сравнивают с параметрами материала, принятого за эталон.
Обрабатываемость давлением определяют в процессе технологических испытаний материалов на пластическую деформацию. Методы оценки обрабатываемости давлением зависят от вида материалов и технологии их переработки. Например, технологические испытания металлов на изгиб проводят, изгибая образцы до заданного угла. Считают, что образец выдержал испытания, если в нем не появилось излома, расслоений, надрывов, трещин. Листы и ленты испытывают на выдавливание с помощью специального пресса. В образце формируют сферическую лунку, прекращая вытяжку в момент достижения текучести материала. Результат определяют по наибольшей глубине лунки в неразрушенных образцах.
Слайд 72
Обрабатываемость давлением порошковых материалов характеризуют их текучестью, уплотняемостью

и формуемостью. Метод определения текучести основан на регистрации времени
истечения навески порошка в процессе его самопроизвольного просыпания через калиброванное отверстие воронки. От этого параметра зависит скорость заполнения порошковыми материалами форм для обработки давлением. Уплотняемость порошка характеризуют зависимостью объема навески порошка от давления − диаграммой прессования. Формуемость − свойство порошкового материала сохранять форму, полученную в процессе прессования.
Литейные характеристики материалов − совокупность технологических показателей, характеризующих формирование отливок путем заливки расплавленных материалов в литейную форму. Жидкотекучесть − свойство расплавленного материала заполнять литейную форму, зависит от вязкости расплава, температур расплава и литейной формы, степени смачивания расплавом стенок формы и т. д. Ее оценивают по длине заполнения расплавом прямолинейного или спирального канала в специальной литейной форме. Усадка литейная − уменьшение объема расплава при переходе из жидкого состояния в твердое. Практически усадку определяют как отношение соответствующих линейных размеров формы и отливки в виде безразмерного коэффициента усадки, индивидуального для каждого материала.