Слайд 2
Исполнитель Робот
Исполнитель Робот умеет перемещаться по лабиринту, начерченному
на плоскости, разбитой на клетки. Между соседними (по сторонам)
клетками может стоять стена, через которую Робот пройти не может.
У Робота есть девять команд. Четыре команды – это команды-приказы: вверх вниз влево вправо
При выполнении любой из этих команд Робот перемещается на одну клетку соответственно:
вверх ↑, вниз ↓, влево ←, вправо →. Если Робот получит команду передвижения сквозь стену, то он разрушится.
Слайд 3
Исполнитель Робот
Также у Робота есть команда закрасить, при
которой закрашивается клетка, в которой Робот находится в настоящий
момент.
Еще четыре команды – это команды проверки условий. Эти команды проверяют, свободен ли путь для Робота в каждом из четырех возможных направлений: сверху свободно снизу свободно слева свободно справа свободно
Эти команды можно использовать вместе с условием «если».
Слайд 4
Исполнитель Робот
Условие «если» имеет следующий вид:
если условие то
последовательность команд
все
Здесь условие – одна из команд проверки условия.
Последовательность команд – это одна или несколько любых команд-приказов.
Слайд 5
Исполнитель Робот
Например, для передвижения на одну клетку вправо,
если справа нет стенки и закрашивания клетки, можно использовать
такой алгоритм:
если справа свободно то
вправо
закрасить
все
В одном условии можно использовать несколько команд проверки условий, применяя логические связки и, или, не, например:
если (справа свободно) и (не снизу свободно) то
вправо
все
Слайд 6
Исполнитель Робот
Для повторения последовательности команд можно использовать цикл
«пока», имеющий следующий вид:
нц пока условие
последовательность команд
кц
Например, для движения вправо, пока это возможно, можно использовать следующий алгоритм:
нц пока справа свободно
вправо
кц
Слайд 7
Задание 1
20.1 Робот находится в левом верхнем углу
огороженного пространства, имеющего прямоугольника. Размеры прямоугольника неизвестны. Где-то посередине
прямоугольника есть вертикальная стена, разделяющая прямоугольник на две части. В этой стене есть проход, при этом проход не является самой верхней или самой нижней клеткой стены. Точное расположение прохода также неизвестно. Одно из возможных расположений стены и прохода в ней приведено на рисунке.
Слайд 8
Задание 1
Напишите для Робота алгоритм, перемещающий Робота в
правый нижний угол прямоугольника.
Алгоритм должен решать задачу для произвольного
размера поля и любого допустимого расположения стены внутри прямоугольного поля. При исполнении алгоритма робот не должен разрушиться.
Слайд 9
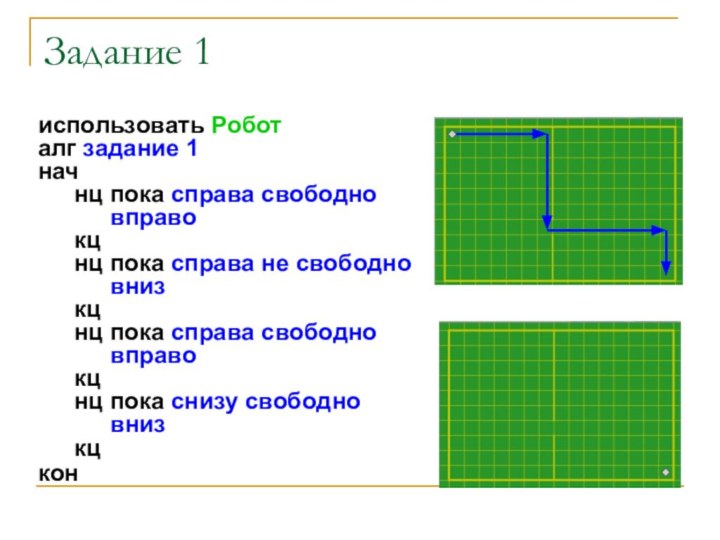
Задание 1
использовать Робот
алг задание 1
нач
нц пока справа свободно
вправо
кц
нц
пока справа не свободно
вниз
кц
нц пока справа свободно
вправо
кц
нц пока снизу
свободно
вниз
кц
кон
Слайд 10
Задание 2
20.1 На бесконечном поле имеется длинная горизонтальная
стена. Длина стены неизвестна. Робот находится в одной из
клеток непосредственно сверху от стены. Начальное положение робота также неизвестно. Одно из возможных положений робота приведено на рисунке.
Слайд 11
Задание 2
Напишите алгоритм для Робота, закрашивающий все клетки,
расположенные выше стены и прилегающие к ней, независимо от
размера стены и начального расположения Робота. Например, для приведенного ранее рисунка Робот должен закрасить следующие клетки:
Конечное расположение Робота может быть произвольным. При исполнении алгоритма Робот не должен разрушиться.
Слайд 12
Задание 2
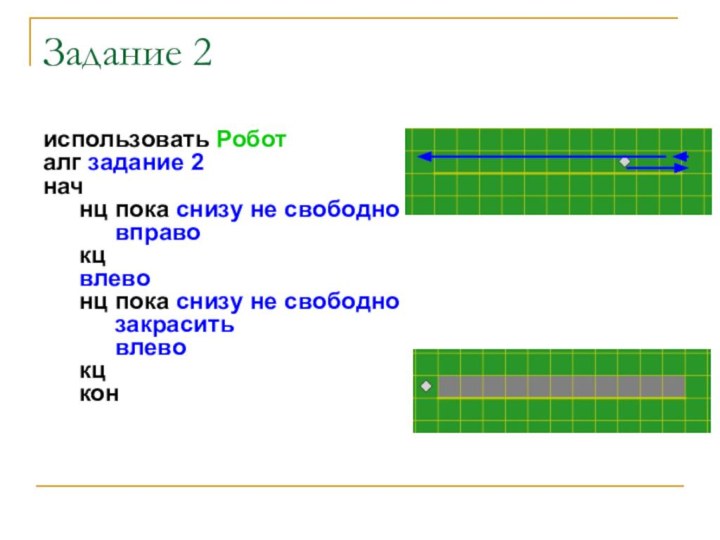
использовать Робот
алг задание 2
нач
нц пока снизу не
свободно
вправо
кц
влево
нц пока снизу не свободно
закрасить
влево
кц
кон
Слайд 13
Задание 3
20.1 На бесконечном поле имеется горизонтальная стена.
Длина стены неизвестна. От правого конца стены вверх отходит
вертикальная стена также неизвестной длины. Робот находится в углу между вертикальной и горизонтальной стеной. На рисунке указан один из возможных способов расположения стен и Робота.
Слайд 14
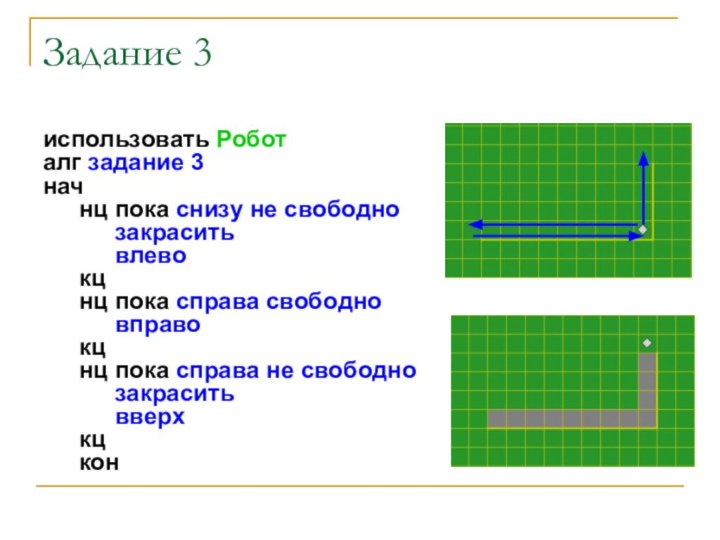
Задание 3
Напишите алгоритм для Робота, закрашивающий все клетки,
расположенные выше горизонтальной стены и левее вертикальной стены и
прилегающие к ним. Робот должен закрасить только клетки, удовлетворяющие заданному условию. Например, для приведенного рисунка Робот должен закрасить следующие клетки:
Конечное расположение
Робота может быть произвольным. При исполнении алгоритма Робот не должен разрушиться.