- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Bridges and Cut Vertices
Содержание
- 2. DefinitionsBridge – an edge of a graph
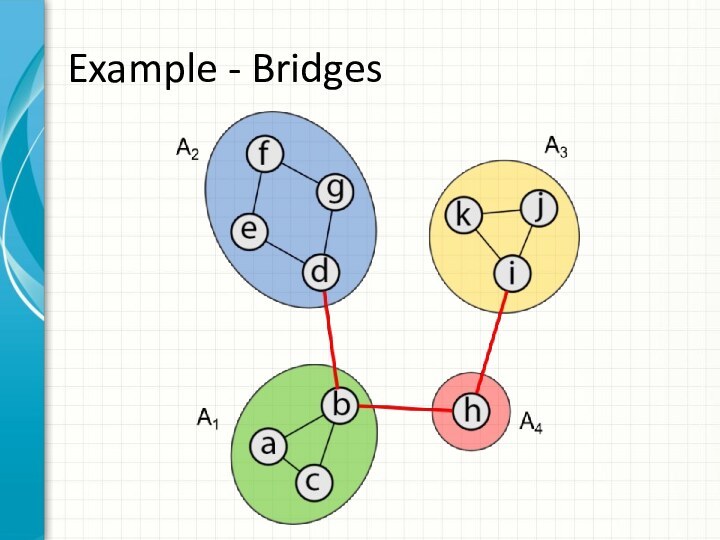
- 3. Example - Bridges
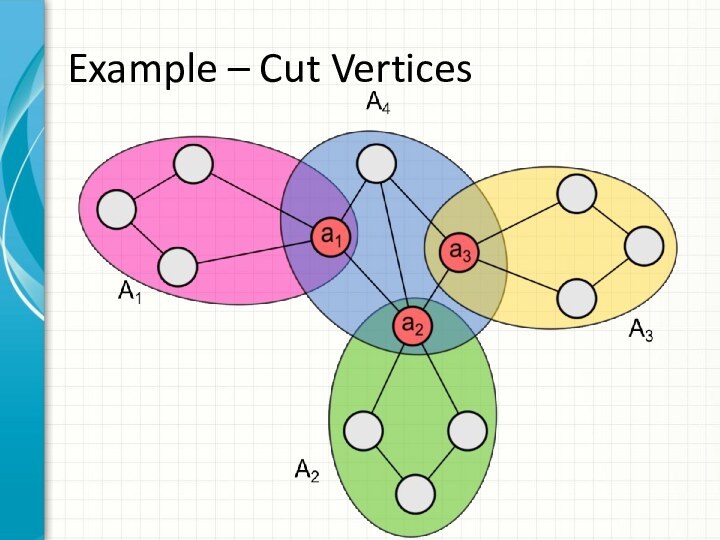
- 4. Example – Cut Vertices
- 5. Definitions for Depth-First-Search in undirected graphTree edge
- 6. Algorithm - Bridges
- 7. Implementation - Bridgesvoid dfs(int v, int p
- 8. Algorithm – Cut Vertices
- 9. Implementation – Cut Verticesvoid dfs(int v, int
- 10. Скачать презентацию
- 11. Похожие презентации
DefinitionsBridge – an edge of a graph whose deletion increases the number of connected components. Cut vertex – a vertex whose deletion increases the number of connected components.



![Bridges and Cut Vertices Implementation - Bridgesvoid dfs(int v, int p = -1) {used[v] = true;tin[v]](/img/tmb/15/1481856/dd4c4332032f22d6f9f819aecd701da2-720x.jpg)

![Bridges and Cut Vertices Implementation – Cut Verticesvoid dfs(int v, int p = -1) {used[v] =](/img/tmb/15/1481856/da266870904a0d776a3a798c1725f4f9-720x.jpg)

Слайд 2
Definitions
Bridge – an edge of a graph whose
deletion increases the number of connected components.
– a vertex whose deletion increases the number of connected components.
Слайд 5
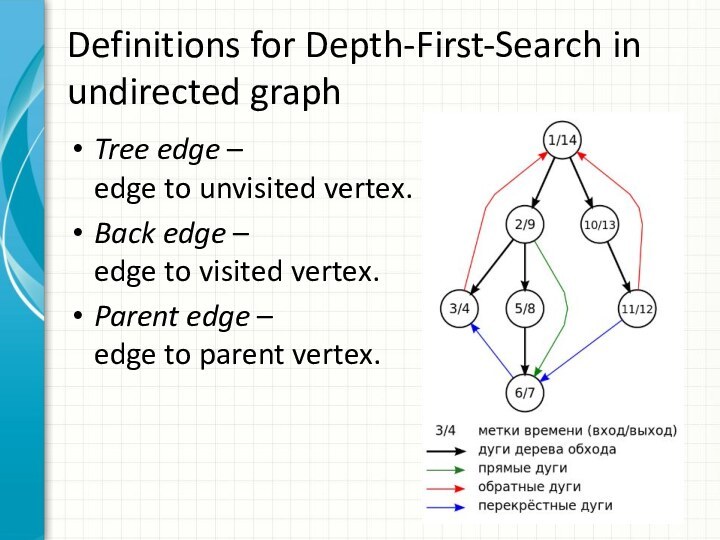
Definitions for Depth-First-Search in undirected graph
Tree edge –
edge to unvisited vertex.
Back edge –
edge to visited
vertex.Parent edge – edge to parent vertex.
Слайд 7
Implementation - Bridges
void dfs(int v, int p =
-1) {
used[v] = true;
tin[v] = fup[v] = timer++;
for (size_t
i = 0; iif (to == p) continue; // Parent edge
if (used[to]) // Back edge
fup[v] = min(fup[v], tin[to]);
else { // Tree edge
dfs(to, v);
fup[v] = min(fup[v], fup[to]);
if (fup[to] > tin[v])
IS_BRIDGE(v, to);
}
}
}
Слайд 9
Implementation – Cut Vertices
void dfs(int v, int p
= -1) {
used[v] = true;
tin[v] = fup[v] = timer++;
int
children = 0; // Number of childrenfor (size_t i = 0; i
if (to == p) continue; // Parent edge
if (used[to]) // Back edge
fup[v] = min(fup[v], tin[to]);
else { // Tree edge
dfs(to, v);
fup[v] = min(fup[v], fup[to]);
if (fup[to] >= tin[v] && p != -1)
IS_CUTPOINT(v);
++children;
}
}
if (p == -1 && children > 1) // If root
IS_CUTPOINT(v);
}