Слайд 2
Основные понятия.
Событие - явление, которое происходит в результате
осуществления какого-либо определенного комплекса условий.
Эксперимент (или
опыт) заключается в наблюдении за объектами или явлениями в строго определенных условиях и измерении значений заранее определенных признаков этих объектов (явлений).
Исходом называется один из взаимоисключающих друг друга вариантов, которым может завершиться случайный эксперимент.
Слайд 3
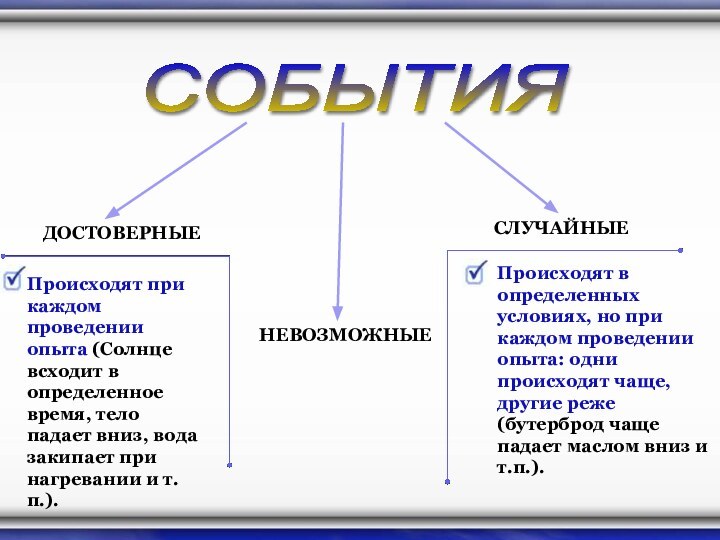
СОБЫТИЯ
ДОСТОВЕРНЫЕ
СЛУЧАЙНЫЕ
Происходят при каждом проведении опыта (Солнце всходит
в определенное время, тело падает вниз, вода закипает при
нагревании и т.п.).
Происходят в определенных условиях, но при каждом проведении опыта: одни происходят чаще, другие реже (бутерброд чаще падает маслом вниз и т.п.).
НЕВОЗМОЖНЫЕ
Слайд 4
Тест 1.
О каком событии идёт речь?
Из 25 учащихся класса двое справляют день рождения 30
февраля.
А) достоверное;
В)невозможное;
С) случайное.
Ответ. В
Слайд 5
Тест 2.
Это событие является
случайным:
А) слово начинается с буквы
«ь»;
В) ученику 8 класса 14 месяцев;
С) бросили две игральные кости: сумма выпавших на них очков равна 8.
Ответ. С
Слайд 6
Тест 3.
Найдите достоверное событие:
А) На уроке математики ученики делали
физические упражнения;
В) Сборная России по футболу не станет чемпионом мира 2006 года;
С) Подкинули монету и она упала на «Орла».
Ответ. В
Слайд 7
Определение
Вероятность события (Р(А)) – это численная мера объективной
возможности его появления.
Вероятностью Р наступления случайного события А
называется отношение m/n, где n – число всех возможных исходов эксперимента, а m – число всех благоприятных исходов:
Р(А)= m/n.
Слайд 8
Классическое определение вероятности было впервые дано в работах
французского математика Лапласа.
Пьер-Симо́н Лапла́с
Слайд 9
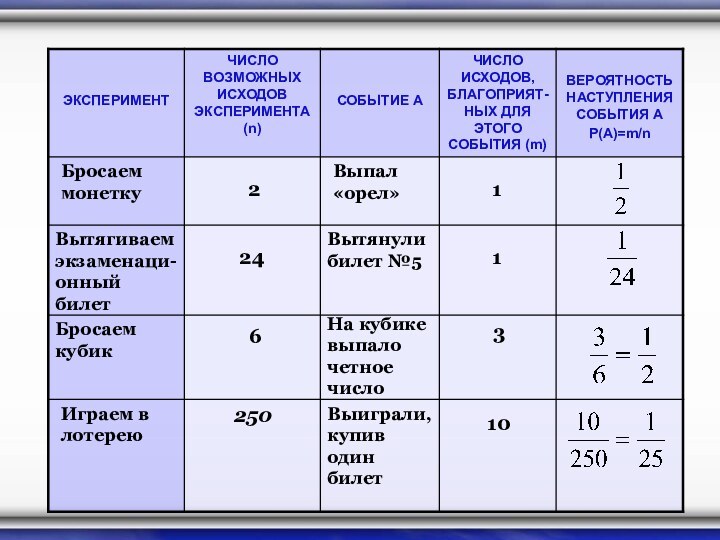
Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем
кубик
На кубике выпало четное число
6
3
Играем в лотерею
Выиграли, купив один
билет
250
10
Слайд 10
Задача 1.
В коробке 4 синих, 3 белых и
2 желтых фишки. Они тщательно перемешиваются, и наудачу извлекается
одна из них. Найдите вероятность того, что она окажется: а) белой; б) желтой; в) не желтой.
Решение.
а) Мы имеем всевозможных случаев 9. Благоприятствующих событий 3. Вероятность равна:P=3:9=1/3=0,33(3)
б) Мы имеем всевозможных случаев 9. Благоприятствующих событий 2. Вероятность равна P=2:9=0,2(2)
в) Мы имеем всевозможных случаев 9. Благоприятствующих событий 7 (4+3). Вероятность равна P=7:9=0,7(7)
Слайд 11
Задача 2.
В коробке лежат 10 одинаковых шаров, на
каждом из которых написан его номер от 1 до
10. Найдите вероятность следующих событий:
а) извлекли шар № 7;
б) номер извлеченного шара – четное число;
в) номер извлеченного шара кратен 3.
Решение. Мы имеем всевозможных случаев 10.
а) Благоприятных 1. Вероятность P=1:10=0,1
б) Шаров с четными номерами 5 (2,4,6,8,10). Вероятность равна P=5:10=0,5
в) Благоприятных 3.(3,6,9). Вероятность равна P=3:10=0,3
Слайд 12
Задача 3.
В урне находятся 3 синих, 8
красных и 9 белых шаров одинакового размера и веса,
неразличимых на ощупь. Шары тщательно перемешаны. Какова вероятность появления синего, красного и белого шаров при одном вынимании шара из урны?
Решение. Так как появление любого шара можно считать равновозможным, то мы имеем всего n=3+8+9=20 элементарных событий. Если через А, В, С обозначить события, состоящие в появлении соответственно синего, красного и белого шаров, а через m1, m2, m3 -числа благоприятствующих этим событиям случаев, то ясно, что m1=3, m2=8, m3=9. Поэтому P(A)=3/20=0,15; P(B)=8/20=0,40; P(C)=9/20=0,45.
Слайд 13
Задача 4.
Таня забыла последнюю цифру номера телефона знакомой
девочки и набрала ее наугад. Какова вероятность того, что
Таня попала к своей знакомой?
Решение. На последнем месте может стоять одна из 10 цифр: от 0 до 9. Значит,
n = 10, m = 1. P (A) = 1/10
Слайд 14
Задача 5.
На четырех карточках написаны буквы О, Т,
К, Р. Карточки перевернули и перемешали. Затем открыли наугад
последовательно эти карточки и положили в ряд. Какова вероятность того, что получится слово «КРОТ»?
Решение. Исходы – все возможные перестановки из четырех элементов. По правилу умножения
n = 4 * 3 * 2 *1 = 24.
Событие А - после открытия карточек получится слово «КРОТ»;
m = 1. (только один вариант расположения букв – «КРОТ»)
P (A) = 1/24.
Слайд 15
Свойства вероятности.
Вероятность достоверного события равна 1
Вероятность невозможного
события равна 0.
Вероятность события А не меньше 0
, но не больше 1.
Слайд 16
Статистическая вероятность
Относительной частотой события А в данной серии
испытаний называют отношение числа испытаний М, в которых это
событие произошло, к числу всех проведённых испытаний N.
Под статистической вероятностью понимают число, около которого колеблется относительная частота события при большом числе испытаний.
Слайд 17
Задача №1
По статистике, на каждые 1000
лампочек приходится 3 бракованные. Какова вероятность купить исправную лампочку?
Решение: Событие А- купить неисправную лампочку
P(A)=3/1000 = 0,003
Вероятность купить исправную лампочку равна 1 – 0,003 = 0,997
Слайд 18
Задача №2.
Демографы утверждают, что вероятность рождения близнецов
равна 0,012. В скольких случаях из 10 000 рождений можно
ожидать появление близнецов?
Решение:
Ответ: в 120 случаях.
Слайд 19
Задача 3.
В классе 20 мальчиков и 10 девочек.
Учитель истории знает, что 3 девочки и 5 мальчиков
из класса были накануне в кино, поэтому не выучили домашнее задание. К сожалению, он не знает их фамилий, но очень хочет поставить кому-нибудь двойку. Кого ему лучше вызвать к доске – мальчика или девочку?
Решение: Общее число исходов для девочек равно 10, для мальчиков – 20. Благоприятных исходов для девочек – 3, для мальчиков – 5, значит для девочек Р(А)=3/10 , для мальчиков-5/20=1/4 .
Так как 3/10 >1/4 , поэтому лучше вызвать девочку.