- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему: Отношение величин (6 класс)
Содержание
- 2. ЦельПознакомиться с понятием отношения величин и его применением на практике.
- 3. Задачи.Изучить использование отношений величин в :математике;географии;физике;искусстве;живой природе; практической деятельности людей.
- 4. ГипотезаПредположим, отношение величин - это только математическое понятие. И в жизни мы его не используем.
- 5. Что такое отношение ?Частное двух чисел
- 6. Как используется отношения ? Учение об
- 7. Что такое число π?Число π –
- 8. Практическое вычисление числа πДля вычисления числа π
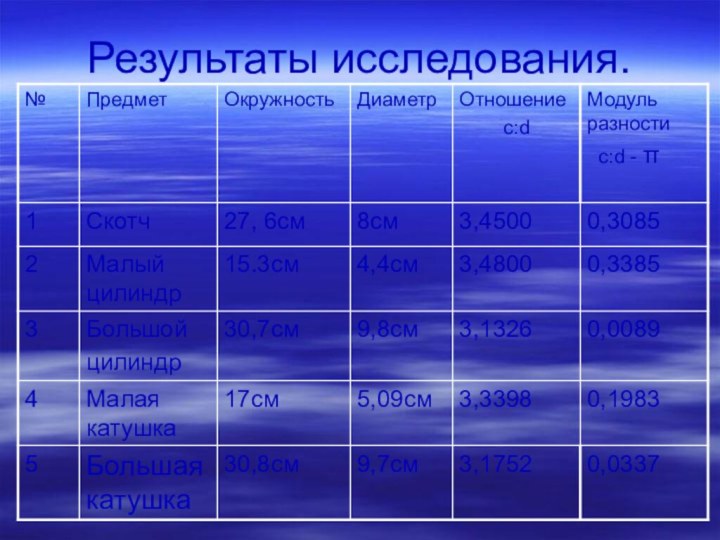
- 9. Практическая работа Мы измерили диаметры и
- 10. Результаты исследования.
- 11. Диаграмма
- 12. Анализ результатовИз диаграммы видно , что ближе
- 13. Метод Бюффона.Наш способ вычисления числа π очень
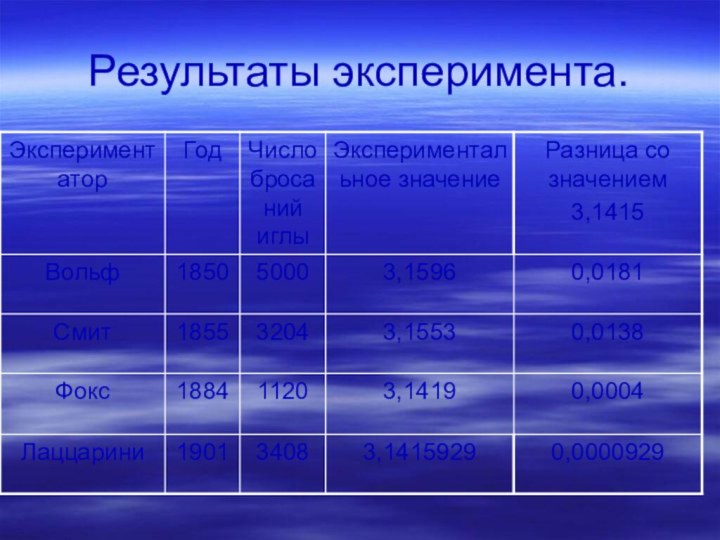
- 14. Результаты эксперимента.
- 15. Ошибки при вычислении числа пи
- 16. Из диаграммы видно , что ближе всего к числу π=3,1415…оказался итальянец Лаццарини.
- 17. Что такое прямая пропорциональная зависимость? Две величины
- 18. МасштабПонятие масштаба тоже связанно с отношением величин.Масштаб
- 19. Для чего используется масштаб?Все мы пользуемся картами
- 20. Практическая работа.Нам нужно нарисовать на обычном
- 21. Итог работыВ итоге нашей работы мы получили план комнаты размером 15x15cм
- 22. Что такое обратная пропорциональная зависимость?Две величины называют
- 23. Практическая работаДля нашей практической работы нам понадобился
- 24. Как мы работаем с рычагом?Кратчайшее расстояние между
- 25. Результат работыРычаг находится в равновесии тогда, когда
- 26. Выводы Применяя правило рычага, можно большей силой
- 27. «Золотое сечение» «Золотое сечение»- это такое
- 28. Где наблюдается «золотое сечение»?Принцип золотого сечения
- 29. Золотое сечение в природе.Расположение листьев на некоторых
- 30. Золотое сечение в архитектуре и искусстве.Храм Парфенон,
- 31. Отношение в фотографияхВсе мы когда-нибудь фотографировались. В
- 32. Отношение и проценты. Отношение одной величины к
- 33. Заключение Наша гипотеза, выдвинутая в начале проекта,
- 34. ЛитератураМатематика 6 класс Виленкин Н.Я. Изд.МНЕМОЗИНА; Журнал
- 35. Спасибо за внимание!
- 36. Скачать презентацию
- 37. Похожие презентации
ЦельПознакомиться с понятием отношения величин и его применением на практике.

































Слайд 3
Задачи.
Изучить использование отношений величин в :
математике;
географии;
физике;
искусстве;
живой природе;
практической
деятельности людей.
Слайд 4
Гипотеза
Предположим, отношение величин - это только математическое понятие.
И в жизни мы его не используем.
Слайд 5
Что такое отношение ?
Частное двух чисел называют
отношением этих чисел.
Отношение показывает, во сколько раз первое
число больше второго, или какую часть первое число составляет от второго.
Слайд 6
Как используется отношения ?
Учение об отношениях появилось
в
IV в. до н.э. в Древней Греции и
дошло до наших дней. Сейчас оно продолжает развиваться, и чаще используется в жизни и практике людей. Теперь рассмотрим использование отношений в математике на примере числа π.
Слайд 7
Что такое число π?
Число π – математическая
константа, выражающая отношение длины окружности к длине её диаметра
c:d
= π. В цифровом выражении начинается как 3,141592… и имеет бесконечную математическую продолжительность.
Как считают специалисты, это число было открыто вавилонскими магами.. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона.
Слайд 8
Практическое вычисление числа π
Для вычисления числа π мы
выполнили практическую работу.
Для этого взяли несколько предметов цилиндрической
формы: скотч, 2 цилиндра,
2 катушки.
Инструменты для измерения и вычисления:
мерная лента, штангенциркуль, калькулятор.
Слайд 9
Практическая работа
Мы измерили диаметры и длины окружностей
выбранных нами предметов. Потом поделили длину окружности на диаметр.
c:d=πРезультаты измерений и вычислений занесли в таблицу.
Слайд 12
Анализ результатов
Из диаграммы видно , что ближе всего
к числу π=3,1415… мы подошли, когда измеряли длины окружностей
и диаметры большого цилиндра и большой катушки
Слайд 13
Метод Бюффона.
Наш способ вычисления числа π очень приближенный
и далеко не единственный. Еще в далеком 1777 году
французский ученый Жорж Бюффон(1707- 1788) опубликовал работу, в которой предложил оценить число π, бросая иголку на специально разрисованную поверхность. Если при бросании обыкновенной иголки на разлинованную доску замечать сколько раз она попадет на одну из прямых, затем результаты подставить в открытую Бюффоном формулур=2L:aπ,
можно вычислить число π с большой точностью.
Слайд 17
Что такое прямая пропорциональная зависимость?
Две величины называют
прямо пропорциональными, если при увеличении (уменьшении) одной из них
в несколько раз другая увеличивается (уменьшается) во столько же раз.Т.е. отношение двух значений одной величины равно отношению двух соответствующих значений другой величины
Примером прямой пропорциональной зависимости является масштаб.
Слайд 18
Масштаб
Понятие масштаба тоже связанно с отношением величин.
Масштаб это
– отношение длины отрезка на карте к длине соответствующего
отрезка на местности.
Слайд 19
Для чего используется масштаб?
Все мы пользуемся картами местности,
но на ней невозможно отобразить натуральную величину объектов. Для
этого нам нужен масштаб. С его помощью мы можем уменьшить величину в нужное нам количество раз.
Слайд 20
Практическая работа.
Нам нужно нарисовать на обычном листе
комнату площадью 3мx3м. Но мы не сможем передать точную
величину комнаты 3мx3м, поэтому ее нужно уменьшить, т.е. мы воспользуемся масштабом 1:20. Чтобы воспользоваться масштабом, уменьшим длину и ширину комнаты в 20 раз, т.е. 3м:20=15см. 3м:20=15см
Слайд 22
Что такое обратная пропорциональная зависимость?
Две величины называют обратно
пропорциональными, если при увеличении (уменьшении) одной из них другая
уменьшается (увеличивается) во столько же раз.Иначе, две величины называют обратно пропорциональными, если отношение двух значений одной величины равно обратному отношению двух соответствующих значений другой величины
Примером обратной пропорциональной зависимости является правило равновесия рычага.
Слайд 23
Практическая работа
Для нашей практической работы нам понадобился рычаг.
Рычаг представляет собой твердое тело, которое может вращаться вокруг
неподвижной опоры.
Слайд 24
Как мы работаем с рычагом?
Кратчайшее расстояние между точкой
опоры и прямой, вдоль которой действует на рычаг сила,
называют плечом силы. Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.
Слайд 25
Результат работы
Рычаг находится в равновесии тогда, когда силы
действующие на него, обратно пропорциональны плечам этих сил. Так
это правило можно записать в виде формулы: F1:F2=L2:L1
Слайд 26
Выводы
Применяя правило рычага, можно большей силой уравновесить
меньшую силу. При этом плечо меньшей силы должно быть
длиннее плеча большей силы (в нашем случае - в 2 раза)
Слайд 27
«Золотое сечение»
«Золотое сечение»- это такое пропорциональное
деление отрезка на неравные части, при котором весь отрезок
так относится к большей части, как сама большая часть относится к меньшей c:b=b:а
Слайд 28
Где наблюдается
«золотое сечение»?
Принцип золотого сечения находит свое
отражение в природе, искусстве, науке, архитектуре, технике, в пропорциях
человеческого тела.
Слайд 29
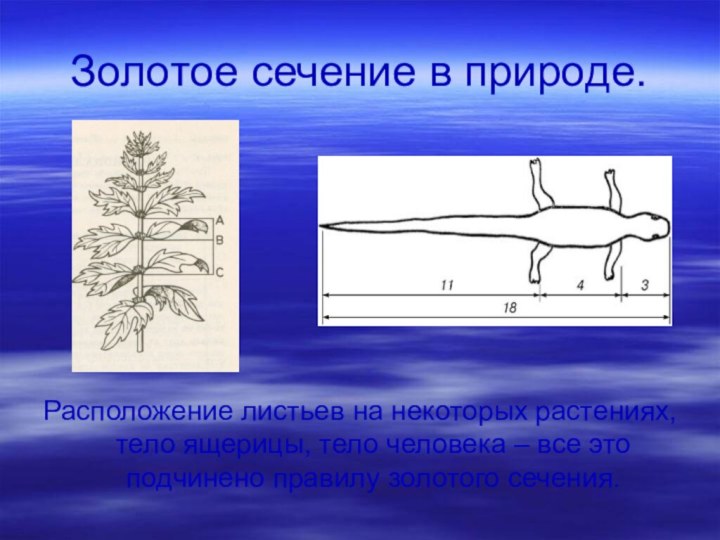
Золотое сечение в природе.
Расположение листьев на некоторых растениях,
тело ящерицы, тело человека – все это подчинено правилу
золотого сечения.
Слайд 30
Золотое сечение в архитектуре и искусстве.
Храм Парфенон,
храм
Василия Блаженного, Смольной собор в Санкт -Петербурге построены по
правилам «золотого сечения». То же самое мы видим в картинах «Корабельная роща», «Пушкин на акте в Лицее», «Пушкин в селе Михайловском».
Слайд 31
Отношение в фотографиях
Все мы когда-нибудь фотографировались. В процессе
фотографирования объекта происходит изменение его размеров в отношении
k=Ro:Rф
,где Ro-размеры объекта , а Rф- соответствующие размеры фотографии. Учитель математики нам сказал , что k называется коэффициентом подобия фигур.