Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему исследовательской работы Закон Бенфорда

Содержание

Мы познаём природы тайны, Что скрыты множеством личин; Явленья жизни не случайны, А цепью связаны причин. Но мы должны признаться честно: В чём жизни суть - нам неизвестно, Хоть повинуется она Давно нам ведомым законам... О,
МБОУ Средняя Общеобразовательная Школа № 41Закон БенфордаНижний Новгород 2014 год Мы познаём природы тайны, Что скрыты множеством личин; Явленья жизни не случайны, История открытия закона.Саймон Ньюкомб (1835-1909 г.) астроном, математик – впервые в 1881г, В 1938 г Френк Бенфорд , аналогичным образом что С. Ньюкомб, обнаружил Числа, начинающиеся с единицы, встречаются гораздо чаще, чем числа, начинающиеся с любой Бенфорд определил вероятность, встретить первую цифру в данных, основанных на Пытаясь выразить обнаруженную закономерность математически, Фрэнк Бенфорд вывел формулу, описывающую вероятность (p) Закон Бенфорда вокруг насДон Лемонс 1986 год: «Луж больше чем озер, озер маленьких вещей в окружающем нас мире всегда больше, чем больших В 1990-е годы Марк Нигрини, поняв, что закону Бенфорда подчиняются бухгалтерские числа, Типы анализа данных по закону БенфордаАнализ частоты первой цифры.Анализ частоты первой и Условия соответствия данных закону Бенфордаданные должны «стремиться» к геометрическому распределениюданные должны относиться Данные соответствующие закону Бенфорда-        номера платежных поручений; -        суммы в авансовых отчетах; Данные не соответствующие закону Бенфорда-        почтовые индексы; -        номера телефонов (первые цифры удивительноПоведение нашей планеты соответствует закону БенфордаПромежуток времени между геомагнитными разворотами Земли, массы Этому закону подчиняется весь мир.Закон Бенфорда – удивительный, прошедший путьот математического курьеза СПАСИБО ЗА ВНИМАНИЕРаботу подготовила:Акимова Ксения6 «А» класс,Руководитель:Данилина М.Ю.
Слайды презентации

Слайд 2 Мы познаём природы тайны,
Что скрыты множеством личин;

Мы познаём природы тайны, Что скрыты множеством личин; Явленья жизни не


Явленья жизни не случайны,
А цепью связаны причин.
Но

мы должны признаться честно:
В чём жизни суть - нам неизвестно,
Хоть повинуется она
Давно нам ведомым законам...
О, сколько надо знать ещё нам,
Чтоб кладезь вычерпать до дна!

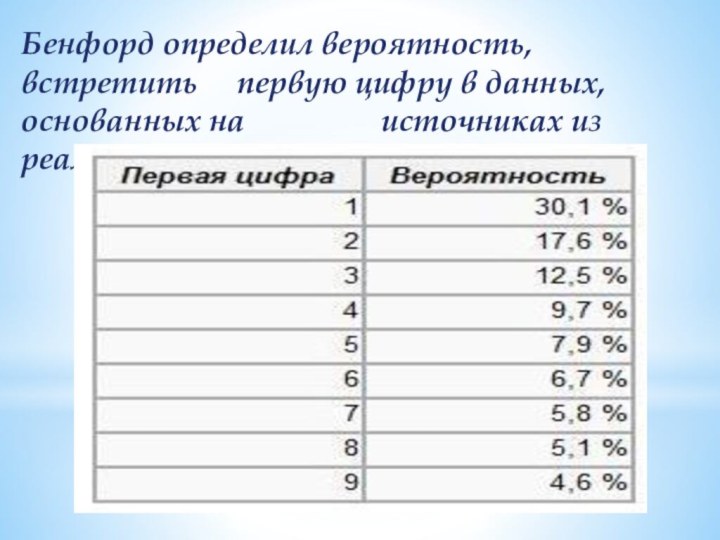
Математика – наука, глубоко проникающая во все сферы жизни человека, находящая отражение в самых заурядных вещах. Закон Бенфорда явное тому подтверждение.

Слайд 3 История открытия закона.
Саймон Ньюкомб (1835-1909 г.) астроном, математик

История открытия закона.Саймон Ньюкомб (1835-1909 г.) астроном, математик – впервые в

– впервые в 1881г, в книге с таблицами логарифмов

заметил «замусоленность» страниц на которых помещались логарифмы чисел, начинающихся с единицы.

Слайд 4 В 1938 г Френк Бенфорд , аналогичным образом

В 1938 г Френк Бенфорд , аналогичным образом что С. Ньюкомб,

что С. Ньюкомб, обнаружил закон аномальных чисел - закон

Бенфорда.

Проанализировав около 20 тысяч содержавшихся в таблицах чисел (площади поверхности 335 рек, удельной теплоемкости и молекулярном весе тысяч химических соединений и даже номера домов улиц из каталога) Бенфорд установил удивительную закономерность.

Слайд 5 Числа, начинающиеся с единицы, встречаются гораздо чаще, чем

Числа, начинающиеся с единицы, встречаются гораздо чаще, чем числа, начинающиеся с

числа, начинающиеся с любой другой цифры. Более того, чем

больше цифра, тем меньше вероятности, что она будет стоять в числе на первом месте.

Слайд 6 Бенфорд определил вероятность, встретить первую цифру в данных,

Бенфорд определил вероятность, встретить первую цифру в данных, основанных на источниках из реальной жизни.

основанных на источниках из

реальной жизни.

Слайд 7 Пытаясь выразить обнаруженную закономерность математически, Фрэнк Бенфорд вывел

Пытаясь выразить обнаруженную закономерность математически, Фрэнк Бенфорд вывел формулу, описывающую вероятность

формулу, описывающую вероятность (p) того, что случайная десятичная дробь

будет начинаться с числа n:

p = lg (n + 1) – lg (n)

Из формулы ясно: чем меньше цифра, тем больше вероятность того, что с нее будет начинаться случайная десятичная дробь.

Слайд 8 Закон Бенфорда вокруг нас
Дон Лемонс 1986 год: «Луж

Закон Бенфорда вокруг насДон Лемонс 1986 год: «Луж больше чем озер,

больше чем озер, озер больше чем морей, а морей

больше чем океанов.»

Слайд 9 маленьких вещей в окружающем нас мире всегда больше,

маленьких вещей в окружающем нас мире всегда больше, чем больших

чем больших

Слайд 10 В 1990-е годы Марк Нигрини, поняв, что закону

В 1990-е годы Марк Нигрини, поняв, что закону Бенфорда подчиняются бухгалтерские

Бенфорда подчиняются бухгалтерские числа, разработал компьютерную программу Digital Analysis

, так появился действенный метод борьбы с фальсификациями и мошенничеством.

Практическое применение закона Бенфорда

Слайд 11 Типы анализа данных по закону Бенфорда
Анализ частоты первой

Типы анализа данных по закону БенфордаАнализ частоты первой цифры.Анализ частоты первой

цифры.
Анализ частоты первой и второй цифры.
Анализ дублей.
Анализ

первой пары цифр.
Анализ первой тройки цифр
Анализ округлений.

Слайд 12 Условия соответствия данных закону Бенфорда
данные должны «стремиться» к

Условия соответствия данных закону Бенфордаданные должны «стремиться» к геометрическому распределениюданные должны

геометрическому распределению
данные должны относиться к одинаковым объектам
не должно быть

ограничений для чисел по max и min
числа не должны быть составными системами

Слайд 13 Данные соответствующие закону Бенфорда
-        номера платежных поручений; -        суммы

Данные соответствующие закону Бенфорда-        номера платежных поручений; -        суммы в авансовых

в авансовых отчетах; -        номера домов в адресах клиентов. -        суммы

бухгалтерских проводок; -        суммы страховых выплат; -        стоимость гарантийного ремонта; -        суммы в налоговых декларациях.

Слайд 14 Данные не соответствующие закону Бенфорда
-        почтовые индексы; -        номера

Данные не соответствующие закону Бенфорда-        почтовые индексы; -        номера телефонов (первые

телефонов (первые цифры – номер АТС); -        выигрышные номера в

лото (здесь цифры – лишь символы, их легко можно заменить, например, на буквы); -        любые ограниченные объемы данных.

Слайд 15 удивительно
Поведение нашей планеты соответствует закону Бенфорда
Промежуток времени между

удивительноПоведение нашей планеты соответствует закону БенфордаПромежуток времени между геомагнитными разворотами Земли,

геомагнитными разворотами Земли, массы планет, глубина землетрясений, продолжительность извержений

вулканов, выбросы парниковых газов и даже статистика инфекционных заболеваний.

Слайд 16 Этому закону подчиняется весь мир.
Закон Бенфорда – удивительный,

Этому закону подчиняется весь мир.Закон Бенфорда – удивительный, прошедший путьот математического


прошедший путь
от математического курьеза до инструмента
серьезных исследований и
ставший

математическим
законом жизненных закономерностей…

  • Имя файла: prezentatsiya-issledovatelskoy-raboty-zakon-benforda.pptx
  • Количество просмотров: 129
  • Количество скачиваний: 0
- Предыдущая Презентация по английскому языку на тему Национальности (5 класс)
Следующая - использование активных форм обучения младших школьников

Похожие презентации

Розв’язування задач на обчислення ймовірностей Розв’язування задач на обчислення ймовірностей 119
Проектная работа. Признаки делимости на 10, на 5 и на 2. Проектная работа. Признаки делимости на 10, на 5 и на 2. 101
Урок математики в 4 классе по программе школа 2000... презентация к уроку по математике (4 класс) Урок математики в 4 классе по программе школа 2000... презентация к уроку по математике (4 класс) 55
Презентация.Таблица умножения на 2 презентация урока для интерактивной доски по математике (2 класс) Презентация.Таблица умножения на 2 презентация урока для интерактивной доски по математике (2 класс) 122
Путешествие в историю чисел Путешествие в историю чисел 119
Первообразная. Правила нахождения первообразных Первообразная. Правила нахождения первообразных 105
Занимательная математика Думай, считай, отгадывай! Занимательная математика Думай, считай, отгадывай! 119
Отчёт по самообразованию Активизация познавательного интереса на уроках математики учебно-методический материал по математике Отчёт по самообразованию Активизация познавательного интереса на уроках математики учебно-методический материал по математике 162
Преобразование целого выражения в многочлен Преобразование целого выражения в многочлен 117
Урок-путешествие по математике. 3-й класс. Тема: Урок-путешествие по математике. 3-й класс. Тема: 106
Презентация к уроку математики в 4 классе презентация к уроку по математике (4 класс) по теме Презентация к уроку математики в 4 классе презентация к уроку по математике (4 класс) по теме 107
Разнообразие математических закономерностей, используемых природой Разнообразие математических закономерностей, используемых природой 186
ИЗМЕРЕНИЕ УГЛОВ. Транспортир ИЗМЕРЕНИЕ УГЛОВ. Транспортир 141
Презентация по математике на тему: Викторина по истории геометрии Презентация по математике на тему: Викторина по истории геометрии 146
Тренажёр по математике 1 класс презентация к уроку по математике (1 класс) Тренажёр по математике 1 класс презентация к уроку по математике (1 класс) 96
Интерактивные игры для детей. презентация урока для интерактивной доски по математике (средняя группа) Интерактивные игры для детей. презентация урока для интерактивной доски по математике (средняя группа) 117
Устный счет по математике Устный счет по математике 109
Дидактическая игра по теме Числовые записи Дидактическая игра по теме Числовые записи 131
Математика Математика 160
Виды часов Виды часов 119
Метод координат Метод координат 119
Презентация к муниципальному МО Система подготовки к ЕГЭ Презентация к муниципальному МО Система подготовки к ЕГЭ 145
Обобщающий урок по теме Действия с десятичными дробями Обобщающий урок по теме Действия с десятичными дробями 157
Презентация по математике Выполни вычитание целых чисел и круглых десятков. Интерактивный тренажёр Презентация по математике Выполни вычитание целых чисел и круглых десятков. Интерактивный тренажёр 105
Блок-схема для решения квадратных неравенств Блок-схема для решения квадратных неравенств 139
Тест по математике для 1го класса презентация урока для интерактивной доски по математике (1 класс) по теме Тест по математике для 1го класса презентация урока для интерактивной доски по математике (1 класс) по теме 139
Презентация Метр 2 класс презентация к уроку по математике (2 класс) Презентация Метр 2 класс презентация к уроку по математике (2 класс) 107
Устный счёт Устный счёт 126
Презентация по математике на темуИсследовательская деятельность как одно из направлений работы с учащимися в условиях реализации ФГОС. Презентация по математике на темуИсследовательская деятельность как одно из направлений работы с учащимися в условиях реализации ФГОС. 94
История развития математики История развития математики 119