- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Математические модели сложных систем
Содержание
- 2. Компьютерное моделирование – математическое моделирование формулируется в
- 4. Математические модели сложных системВебинар № 4Основные понятия сложных систем.Методы моделирования сложных систем.
- 5. Элемент
- 6. Структура
- 7. Понятие математического моделирования
- 8. Общая схема ММ функционирования системы: Множество
- 9. Задачи исследования систем: анализ – изучение свойств
- 15. Детерминированные объекты, функционирующие в дискретном времени, описываются математическими моделями, сводящимися к различным типам конечных автоматов.
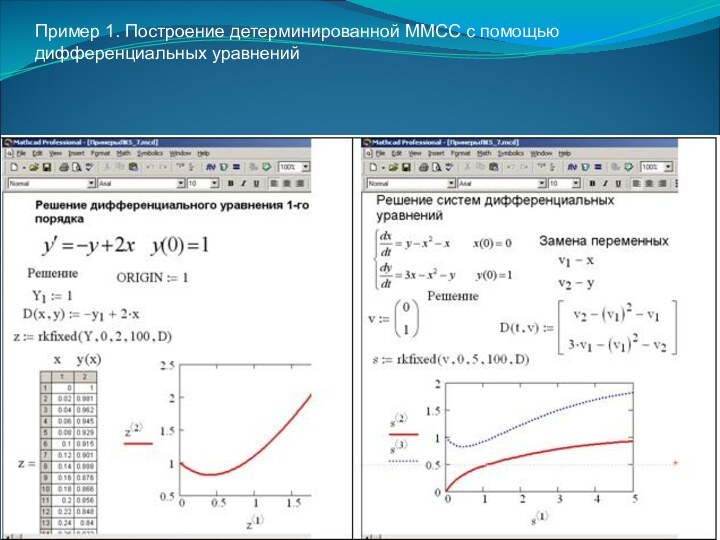
- 19. Пример 1. Построение детерминированной ММСС с помощью дифференциальных уравнений
- 20. Пример 2. Построение стохастической ММСС с применением аппарата СМО
- 22. Автор: Орлова И.В., Половников В.А. Издательство: Вузовский
- 23. Скачать презентацию
- 24. Похожие презентации
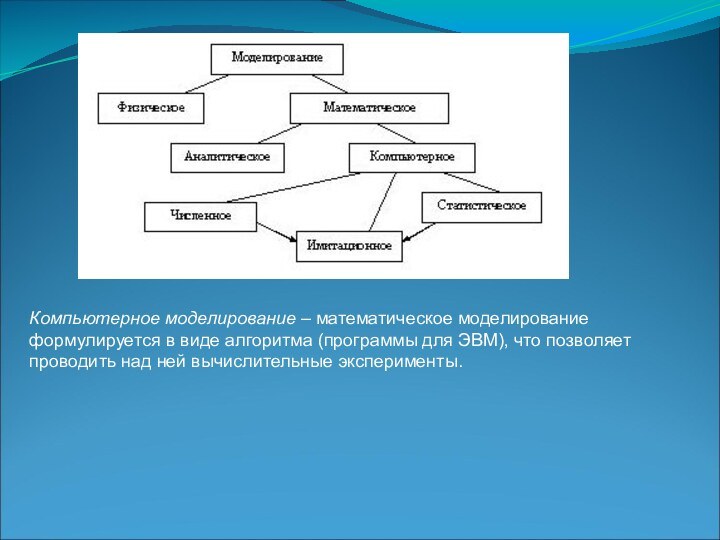
Компьютерное моделирование – математическое моделирование формулируется в виде алгоритма (программы для ЭВМ), что позволяет проводить над ней вычислительные эксперименты.
















![Математические модели сложных систем Анфилатов, В. С. Системный анализ в управлении [Текст]: учеб.пособие / В. С.](/img/tmb/15/1446784/c338b24a1ee8591980cfe45a12de66e1-720x.jpg)
Слайд 4
Математические модели сложных систем
Вебинар № 4
Основные понятия сложных
систем.
Методы моделирования сложных систем.
Слайд 5 Элемент s
– некоторый объект, обладающий определенными свойствами, внутреннее строение которого
для целей исследования не играет роли (самолет: для моделирования полета – не элемент (надсистема), а для моделирования работы аэропорта –элемент).Связь l между элементами – процесс их взаимодействия, важный для целей исследования.
Система S – совокупность элементов со связями и целью функционирования F.
Сложная система – состоящая из разнотипных элементов с разнотипными связями.
Большая система – состоящая из большого числа однотипных элементов с однотипными связями.
Система:
Автоматизированная система - сложная система с определяющей ролью элементов двух типов: технических средств (прежде всего ЭВМ) и действий человека :
здесь - остальные элементы системы.
Слайд 6 Структура системы
– ее расчленение (декомпозиция) на элементы или группы элементов
с указанием связей между ними, неизменное во время функционирования системы.Практически все системы рассматриваются функционирующими во времени, поэтому определим их динамические характеристики.
Состояние – множество характеристик элементов системы, изменяющихся во времени и важных для целей функционирования.
Процесс (динамика) – множество значений состояний системы, изменяющихся во времени.
Цель функционирования – задача получения желаемого состояния системы. Достижение цели обычно влечет целенаправленное вмешательство в процесс функционирования системы, которое называется управлением.
Слайд 7
Понятие математического моделирования
Построение модели начинается с определения параметров и переменных, определяющих процесс функционирования системы.
Параметры системы - характеристики системы, остающиеся постоянными на всем интервале T.
Если , то говорят, что имеется параметрическое семейство систем.
Переменные – зависимые и независимые.
Независимые:
входные воздействия (в т.ч. управляющие):
воздействия внешней среды (контролируемые – неконтролируемые = наблюдаемые – ненаблюдаемые и детерминированные – случайные):
состояния системы
Зависимые – выходные характеристики (сигналы)
Слайд 8
Общая схема ММ функционирования системы:
Множество переменных
вместе
с законами функционированияназывается математической моделью системы.
Если t непрерывно, то модель называется непрерывной, иначе – дискретной
Если модель не содержит случайных элементов, то она называется детерминированной, в противном случае – вероятностной.
Слайд 9
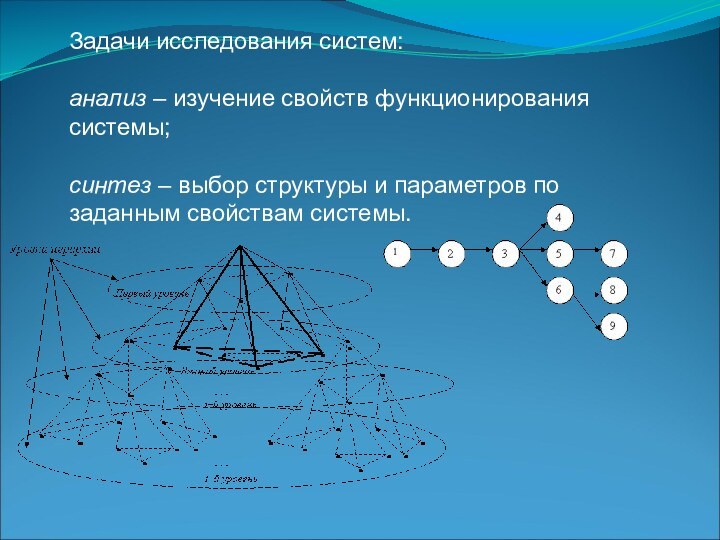
Задачи исследования систем:
анализ – изучение свойств функционирования
системы;
синтез – выбор структуры и параметров по заданным свойствам
системы.Слайд 10 При
построении математических моделей сложных технических систем эффективным оказывается их
последовательное расчленение на подсистемы (декомпозиция системы) с сохранением связей между выявленными подсистемами. Процедура декомпозиции осуществляется до получения таких подсистем, которые в условиях рассматриваемой задачи будут признаны достаточно простыми и удобными для непосредственного математического описания. Эти подсистемы, не подлежащие дальнейшей декомпозиции, называются элементами сложной системы.Таким образом, в общем случае сложная система является многоуровневой иерархической конструкцией из взаимодействующих элементов, объединяемых в подсистемы различных уровней. Представление моделируемого объекта в виде многоуровневой системы называется его структуризацией.
Математическая модель сложной системы образуется композицией (в рамках выделенной структуры) математических моделей элементов и взаимодействий между ними.
Слайд 11
При построении математической модели сложной системы необходимо учитывать взаимодействие
её с внешней средой. Внешняя среда рассматривается как некоторая совокупность объектов, воздействующих на элементы сложной системы, а также испытывающих воздействия, поступающие от элементов сложной системы. Механизм обмена сигналами и формализованная схема взаимодействия элементов сложной системы между собой и с объектами внешней среды включает наборы следующих составляющих:1. процесс формирования выходного сигнала соответствующим элементом системы;
2. определение адреса передачи для каждого выходного сигнала;
3. прохождение сигналов по каналам связи и компоновка входных сигналов для элементов системы, принимающих сигналы.
4. реагирование элементов на поступающие входные сигналы.
Первая и четвертая составляющие описываются в рамках математических моделей элементов. Третья составляющая связана с заменой реальных физических каналов идеальными. Вторая составляющая механизма обмена сигналами в сложной системе обеспечивает адресацию характеристик выходных сигналов и их компоновку во входные сигналы элементов, т.е. схему сопряжения элементов (иногда говорят структуру связности).
Слайд 12 Математическим
описанием элементов сложной системы на единой концептуальной основе и
построением соответствующей схемы сопряжения элементов исчерпывается проблема построения математической модели функционирования сложной системы.Для моделирования технических систем в настоящее время успешно применяются структурные методы, теория автоматического управления, методы электрического аналогизирования, метод графов связей, метод, использующий библиотеку моделей компонентов – элементов и связей, тензорные методы и др.
Слайд 13 При
построении математических моделей сложных технических систем эффективным оказывается их
последовательное расчленение на подсистемы (декомпозиция системы) с сохранением связей между выявленными подсистемами. Процедура декомпозиции осуществляется до получения таких подсистем, которые в условиях рассматриваемой задачи будут признаны достаточно простыми и удобными для непосредственного математического описания. Эти подсистемы, не подлежащие дальнейшей декомпозиции, называются элементами сложной системы.Таким образом, в общем случае сложная система является многоуровневой иерархической конструкцией из взаимодействующих элементов, объединяемых в подсистемы различных уровней. Представление моделируемого объекта в виде многоуровневой системы называется его структуризацией. Математическая модель сложной системы образуется композицией (в рамках выделенной структуры) математических моделей элементов и взаимодействий между ними.
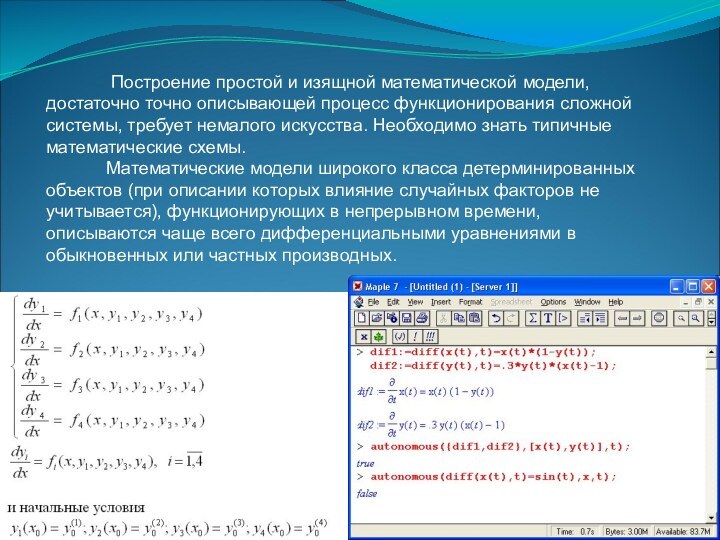
Слайд 14 Построение
простой и изящной математической модели, достаточно точно описывающей процесс
функционирования сложной системы, требует немалого искусства. Необходимо знать типичные математические схемы.Математические модели широкого класса детерминированных объектов (при описании которых влияние случайных факторов не учитывается), функционирующих в непрерывном времени, описываются чаще всего дифференциальными уравнениями в обыкновенных или частных производных.
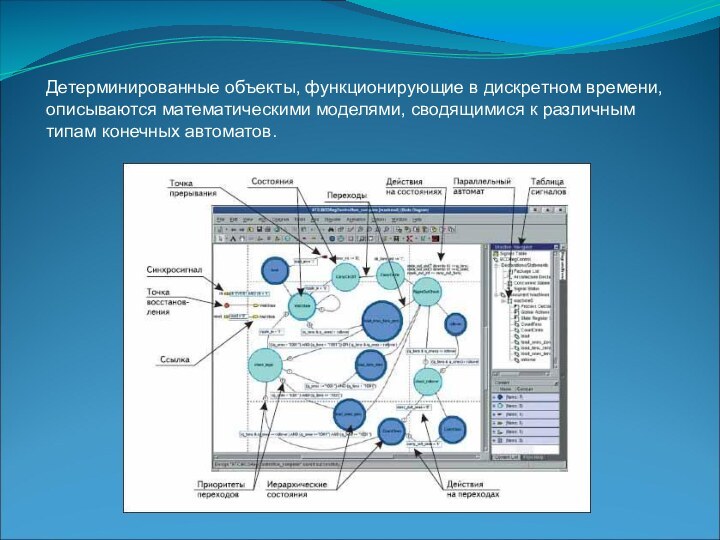
Слайд 15 Детерминированные объекты, функционирующие в дискретном времени, описываются математическими
моделями, сводящимися к различным типам конечных автоматов.
Слайд 16 Автомат
можно представить как некоторое устройство (черный ящик), на которое
подаются дискретные входные воздействия (сигналы) и с которого снимаются дискретные выходные воздействия; оно имеет также некоторые внутренние состояния. Автомат функционирует в дискретном автоматном времени, моментами которого являются такты, т.е. примыкающие друг к другу равные интервалы времени, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния. Обозначим состояние, а также входной и выходной сигналы, соответствующие t-тому такту при t = 0,1,2,… через z(t), x(t), y(t). При этом, по условию z(0) = z0, a z(t) Z, x(t)X, y(t)Y. Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент t = 0,1,2,…дискретного времени автомат находится в определенном состоянии z(t) из множества Z состояний автомата, причем в начальный момент времени t = 0 он всегда находится в начальном состоянии z(0) = z0.Слайд 17
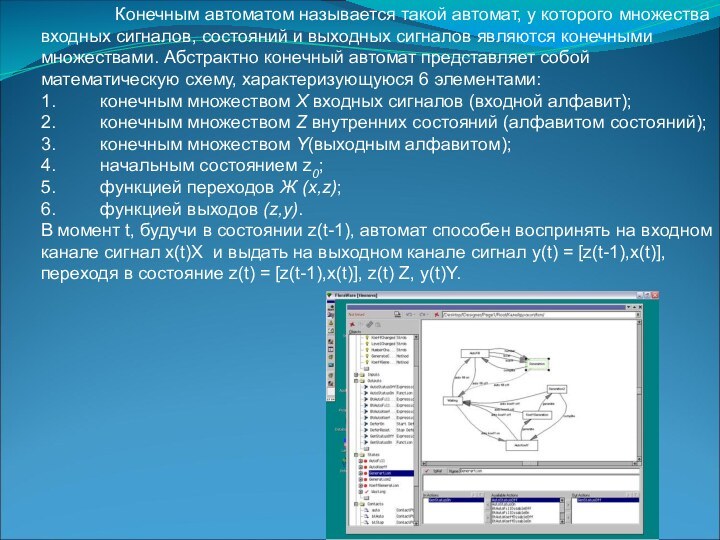
Конечным автоматом называется такой автомат, у которого множества входных
сигналов, состояний и выходных сигналов являются конечными множествами. Абстрактно конечный автомат представляет собой математическую схему, характеризующуюся 6 элементами:1. конечным множеством X входных сигналов (входной алфавит);
2. конечным множеством Z внутренних состояний (алфавитом состояний);
3. конечным множеством Y(выходным алфавитом);
4. начальным состоянием z0;
5. функцией переходов Ж (x,z);
6. функцией выходов (z,y).
В момент t, будучи в состоянии z(t-1), автомат способен воспринять на входном канале сигнал x(t)X и выдать на выходном канале сигнал y(t) = [z(t-1),x(t)], переходя в состояние z(t) = [z(t-1),x(t)], z(t) Z, y(t)Y.
Слайд 18
Стохастические объекты (при моделировании которых учитываются случайные факторы), функционирующие
в дискретном времени, можно представить вероятностными автоматами. Для такого автомата состояние z(t-1) и входной сигнал x(t) определяют не конечное состояние z(t), а распределение вероятностей Pij перехода автомата из состояния zi = z(t-1) в одно из возможных состояний zj(t) в момент времени t под воздействием входного сигнала x(t) .Функция переходов вероятностного автомата определяет не одно конкретное состояние, а лишь распределение вероятностей на множестве состояний (автомат со случайными переходами), а функция выходов – распределение вероятностей на множестве выходных сигналов (автомат со случайными выходами). Функционирование вероятностных автоматов изучается при помощи аппарата цепей Маркова.
Математическими моделями стохастических объектов с непрерывным временем являются системы массового обслуживания (представители марковских случайных процессов).
Слайд 21 Взаимодействие
элементов в процессе функционирования сложной системы рассматривается как результат
совокупности воздействий каждого элемента на другие элементы.Воздействие представленное набором своих характеристик, часто называют сигналом, т.о. взаимодействие элементов сложной системы может быть рассмотрено в рамках механизма обмена сигналами. Сигналы передаются по каналам связи между элементами. Начало данного канала – выходной полюс, конец канала – входной полюс элемента.
Идеальным каналом называется канал, в котором передача сигнала осуществляется мгновенно и без искажений. Полностью и правильно формализованная система имеет только идеальные каналы связей.
Слайд 22
Автор: Орлова И.В., Половников В.А.
Издательство: Вузовский учебник
Год: 2008
В.В.
Васильев, Л.А. Симак, А.М. Рыбникова. Математическое и компьютерное моделирование
процессов и систем в среде MATLAB/SIMULINK. Учебное пособие для студентов и аспирантов. 2008 год. 91 стр.Компьютерное моделирование физических задач в Microsoft Visual Basic. Учебник Author: Алексеев Д.В.
СОЛОН-ПРЕСС, 2009 г