- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Предел функции
Содержание
- 2. Бесконечные величины и правила работы с ними.Бесконечно
- 3. Две бесконечно малые величины называются величинами одного
- 4. Правила работы с бесконечными величинами
- 7. Предел функцииПредел функции при
- 8. Из приведенной таблицы и графика видно, что
- 9. Обозначение пределаНаправление предела (к чему стремится х)ФункцияЗначение предела
- 11. Аналогично вводится понятие предела функции в общем
- 13. Теоремы о пределахПредел постоянного равен этому постоянному.Предел
- 14. Теоремы о пределах3. Предел произведения двух функций
- 15. Следствия из теорем о пределахПостоянный множитель можно вынести за знак предела.Если n – натуральное число то:
- 16. 3. Предел многочлена (целой рациональной функции)
- 17. 4. Предел дробно-рациональной функции при
- 19. При решении задач на поиск пределов функции
- 20. Производная
- 21. Задача о скорости движенияПусть тело движется прямолинейно
- 22. За промежуток времени от t до t+∆t
- 23. Чем меньше промежуток ∆t, тем точнее средняя
- 24. Определение производнойПроизводной функции
- 25. Общее правило поиска производнойПусть дана функция f(x),
- 26. 2. Найдем приращение (изменение) функции.∆y=f(x+ ∆x)-f(x)3. Найдем
- 27. Рассмотрим пример
- 30. Таблица производных
- 31. Основные правила дифференцирования.Пусть заданы две функции u(x)
- 32. 3. Производная частного двух функций4. Производная сложной
- 33. Дифференциал функцииДифференциалом функции f(x) в точке х
- 34. Численные методы дифференцирования
- 35. f(x)f(x+Δx)
- 36. Геометрическим смыслом производной в данной точке является
- 38. Производные высших порядков
- 39. Использование производной для решения задач на экстремум
- 42. В общем случае задачи на экстремум решаются
- 43. Применение производной для исследования функции.Производные при исследовании
- 44. 1. Для определения участков возрастания, уменьшения и постоянства функции, воспользуемся следующими признаками
- 45. 2. Для поиска критических точек находят точки в которых производная функции равна нулю или не существует.
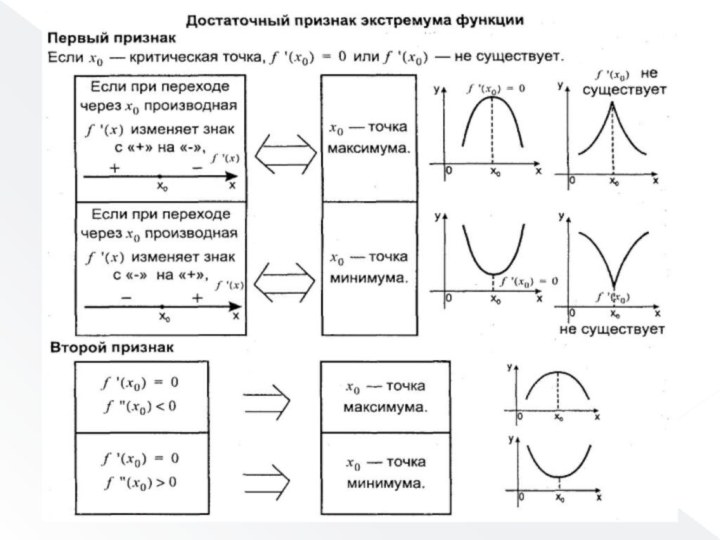
- 46. 3. Поиск точек экстремумов функции производят среди критических точек
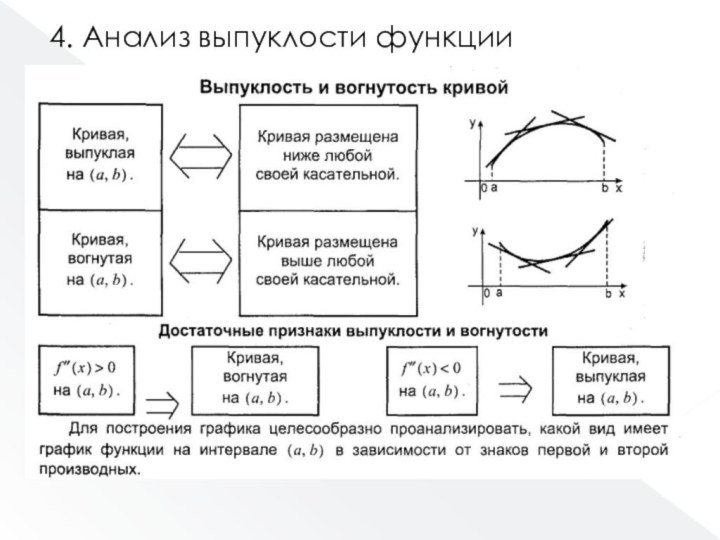
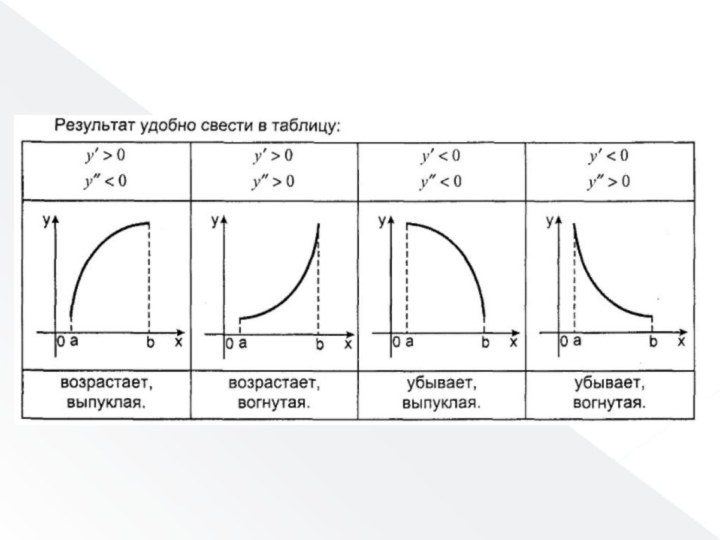
- 48. 4. Анализ выпуклости функции
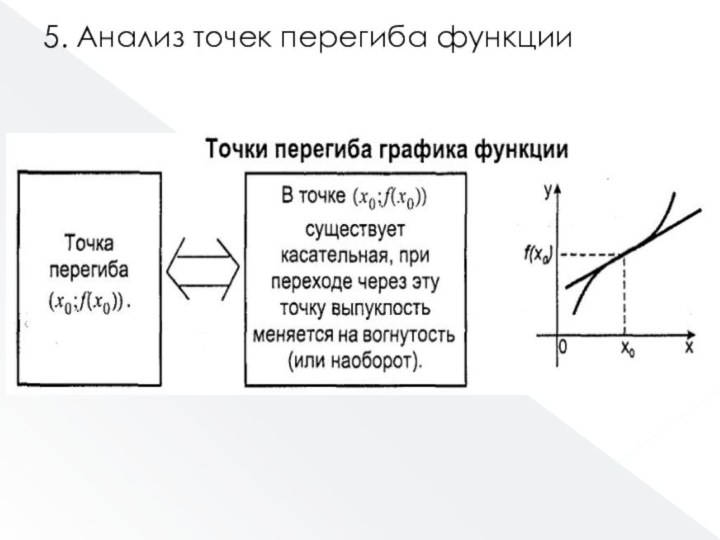
- 50. 5. Анализ точек перегиба функции
- 51. Достаточный признак точки перегиба.В точке (x0;f(x0)) существует
- 52. Скачать презентацию
- 53. Похожие презентации
Бесконечные величины и правила работы с ними.Бесконечно большим или просто бесконечным, называется переменное число, стремящееся превзойти по абсолютной величине всякую границу, как бы велика она не была, а бесконечно малым называют всякое переменное число, имеющее пределом








































Слайд 3 Две бесконечно малые величины называются величинами одного и
того же порядка, если их отношение стремится к конечному
пределу, отличному от нуля.Если же отношение одной бесконечно малой величины β к другой α стремится к нулю, то говорят, что β бесконечно малая более высокого порядка, чем α.
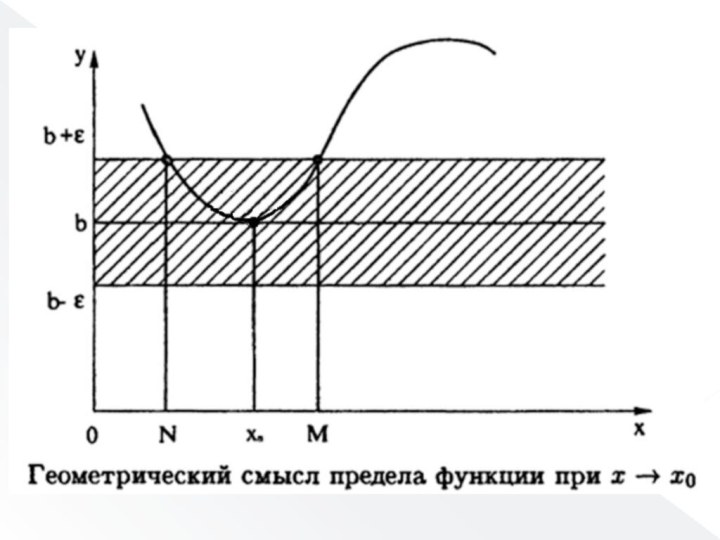
Слайд 8 Из приведенной таблицы и графика видно, что значение
функции при росте значения аргумента постепенно приближается к 2.
Таким
образом для функции может быть введено понятие предела функции. Определение предела при
Число b называется пределом функции y=f(x) при ,
если каково бы ни было положительное число ε можно найти такое N, что для всех х>N выполняется неравенство
Символическая запись такого предела выглядит так:
Слайд 11
Аналогично вводится понятие предела функции в общем случае
Число
b является пределом функции
при
, если каково бы ни было значение ε, можно найти такие N и M, что для всех х, лежащих в интервале (N; M) (за исключением, быть может, точки х0), выполняется неравенство
Символическая запись предела функции при
Слайд 13
Теоремы о пределах
Предел постоянного равен этому постоянному.
Предел алгебраической
суммы двух функций равен алгебраической сумме пределов от этих
функций.
Слайд 14
Теоремы о пределах
3. Предел произведения двух функций равен
произведению пределов от этих функций.
4. Предел частного двух функций
равен частному пределов от этих функций при условии, что предел знаменателя не равен нулю
Слайд 15
Следствия из теорем о пределах
Постоянный множитель можно вынести
за знак предела.
Если n – натуральное число то:
Слайд 16
3. Предел многочлена (целой рациональной функции)
при
равен значению этого многочлена
при х=а.
Слайд 17
4. Предел дробно-рациональной функции
при
, равен значению этой функции
при х=а, при условии что а входит в область допустимых значений функции.Слайд 19 При решении задач на поиск пределов функции необходимо
обращать внимание на возникновении неопределенностей. В этом случае для
решения задач необходимо применять специальные методы.
Слайд 21
Задача о скорости движения
Пусть тело движется прямолинейно и
задан закон его движения
, т.е. известно расстояние s точки от некоторого начала отсчета в каждый момент времени t.В момент времени t пройденное расстояние равно s(t), в момент времени t+∆t расстояние равно s(t+ ∆t)
Слайд 22 За промежуток времени от t до t+∆t т.е.
за время ∆t тело пройдет расстояние
∆s=s(t+∆t )-s(t).
Средняя
скорость движения за промежуток времени ∆t будетСредняя скорость в момент времени t в общем случае зависит от ∆t.
Слайд 23 Чем меньше промежуток ∆t, тем точнее средняя скорость
будет соответствовать реальной скорости тела в момент времени t.
В
предельном случае можно записать Пределы подобного вида очень часто встречаются в математике. Это привело в возникновению понятия производной.
Слайд 24
Определение производной
Производной функции в
точке х называется предел отношения приращения(изменения) функции к приращению
(изменению) аргумента, при стремлении изменения аргумента к нулю, если этот предел существует
Слайд 25
Общее правило поиска производной
Пусть дана функция f(x), непрерывная
и определенная в некоторой области. Необходимо найти производную этой
функции.Придадим аргументу х некоторое приращение (изменение) ∆х и подставим в выражение функции вместо х новое значение х+∆х. Найдем новое измененное значение функции при новом значении аргумента.
y+ ∆y=f(x+ ∆х)
Слайд 26
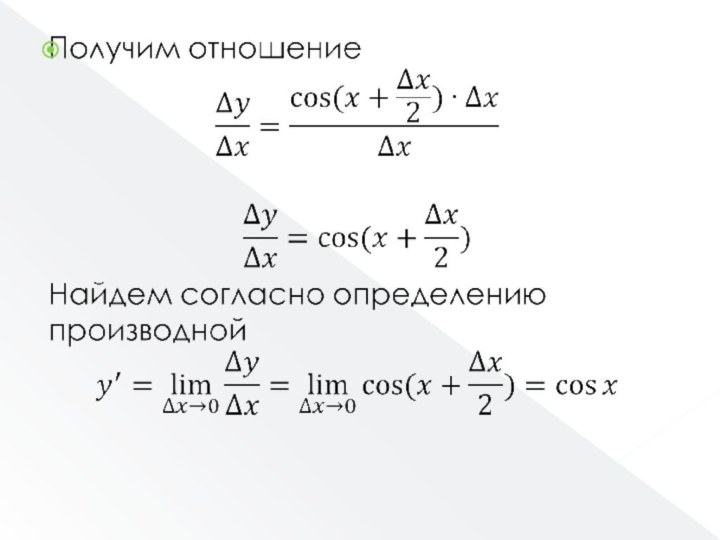
2. Найдем приращение (изменение) функции.
∆y=f(x+ ∆x)-f(x)
3. Найдем отношение
приращения функции к приращению аргумента
4. Находим предел полученного отношения
при Этот предел и есть производная исходной функции f(x)
Слайд 31
Основные правила дифференцирования.
Пусть заданы две функции u(x) и
v(x).
Производная алгебраической суммы двух функций
Производная произведения двух функций.
Слайд 32
3. Производная частного двух функций
4. Производная сложной функции.
Пусть
тогда говорят, что y является сложной функцией. Её производная находится по формуле
Слайд 33
Дифференциал функции
Дифференциалом функции f(x) в точке х называется
главная, линейная относительно ∆х, часть приращения функции
При
можно записать дифференциал в видеИ следовательно производную
можно записать в виде
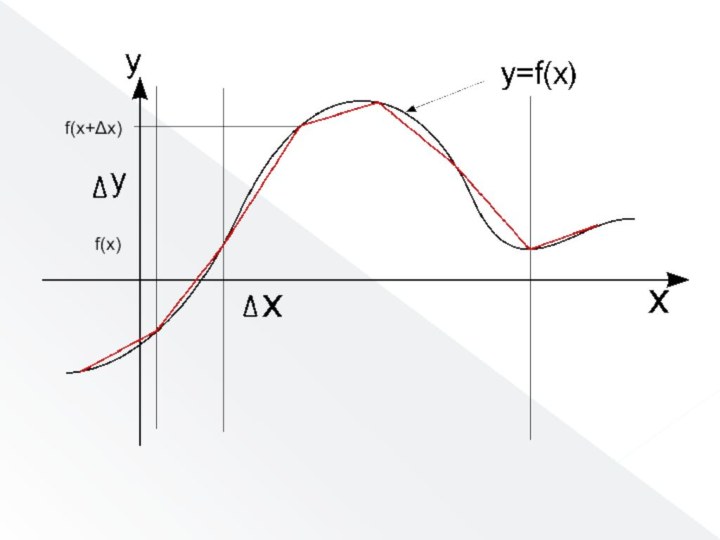
Слайд 36 Геометрическим смыслом производной в данной точке является тангенс
угла наклона касательной проведенной к графику функции через данную
точку.На этом основан геометрический метод дифференцирования.
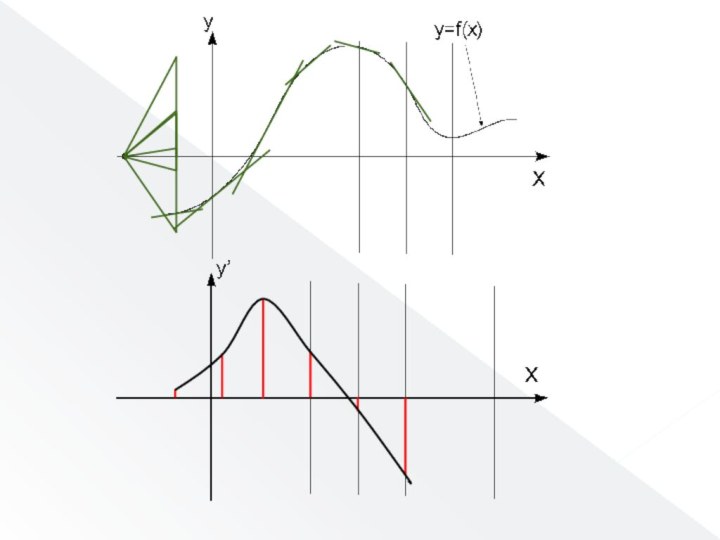
Геометрические методы дифференцирования
Слайд 39
Использование производной для решения задач на экстремум функции
Задача
о квадратном ведре.
Дан квадратный лист металла с ребром равным
а. По углам листа делают вырезы размером х, сгибают лист по вырезам и запаивают швы, получается квадратное ведро. Необходимо узнать при какой величине выреза х объем ведра будет максимальныйa
x
Слайд 42 В общем случае задачи на экстремум решаются в
следующей последовательности:
Составляется уравнение в левой части которого находится величина
экстремум которой ищется, а в правой переменная от которой этот экстремум зависит.Находится производная полученной функции и приравнивается к нулю
Решается полученное уравнение относительно переменной.
Анализируется полученные решения.
Слайд 43
Применение производной для исследования функции.
Производные при исследовании функций
используются для:
1. Определения интервалов возрастания и убывания функции.
2. Поиска
точек максимумов и минимумов функции, точек перегибов функции.3. Поиска участков выпуклости и вогнутости исследуемой функции
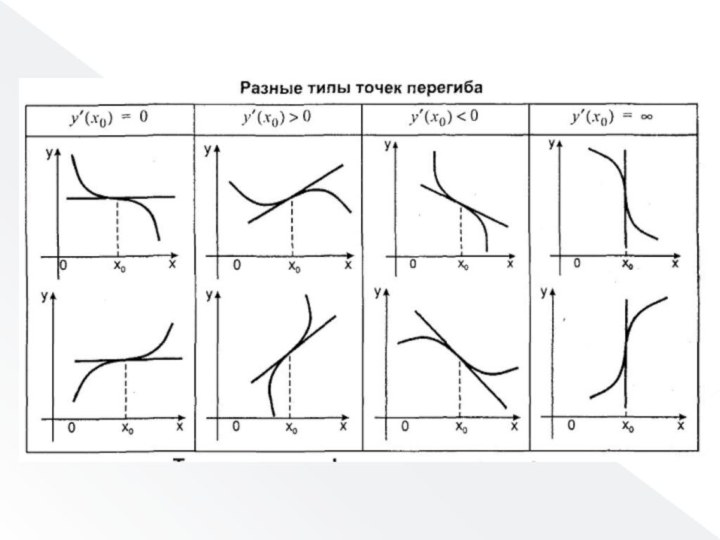
4. Поиска точек перегиба функции(если они есть)
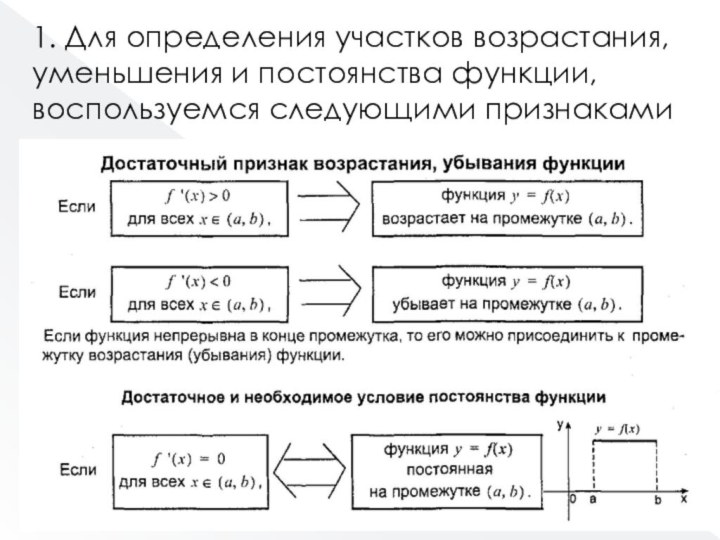
Слайд 44 1. Для определения участков возрастания, уменьшения и постоянства
функции, воспользуемся следующими признаками
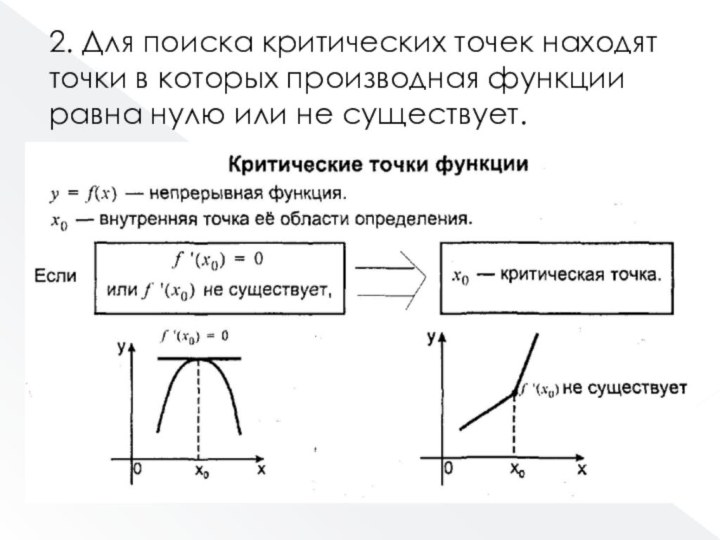
Слайд 45 2. Для поиска критических точек находят точки в
которых производная функции равна нулю или не существует.
Слайд 51
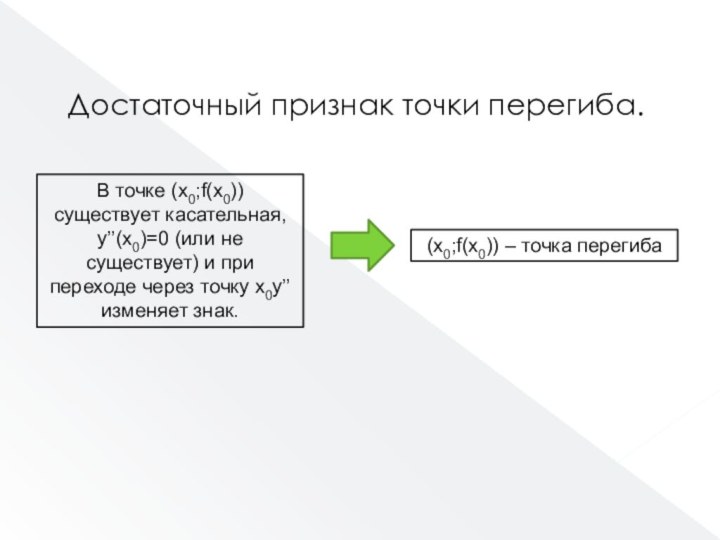
Достаточный признак точки перегиба.
В точке (x0;f(x0)) существует касательная,
y’’(x0)=0 (или не существует) и при переходе через точку
x0y’’ изменяет знак.(x0;f(x0)) – точка перегиба