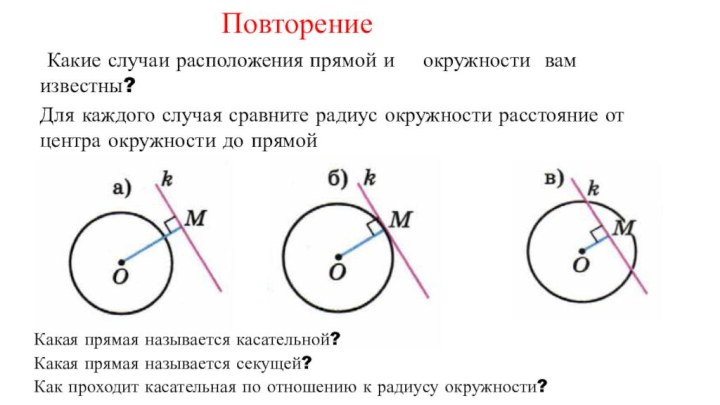
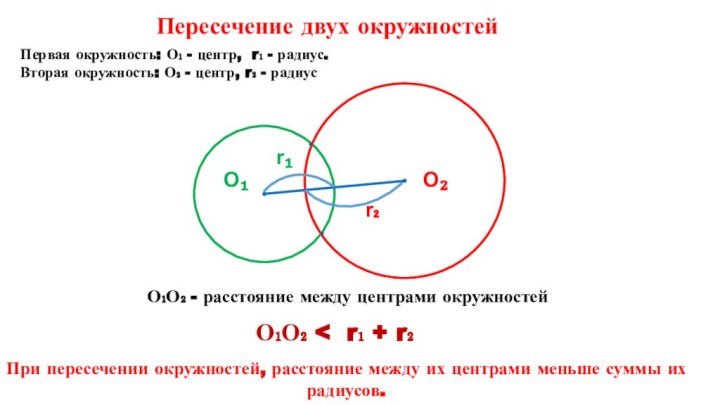
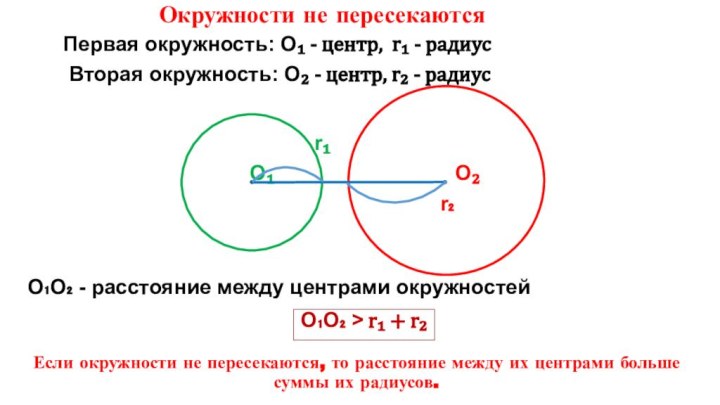
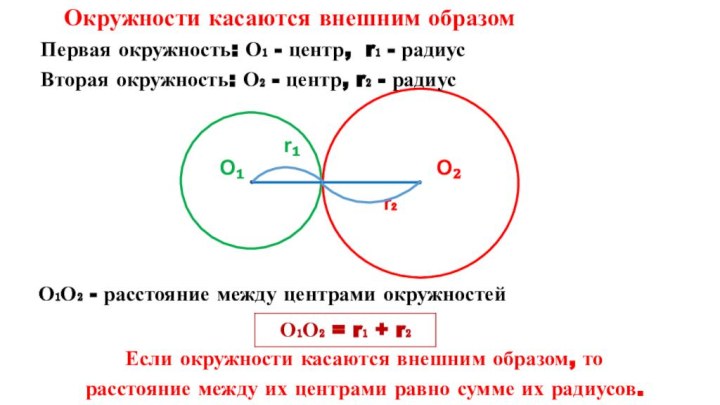
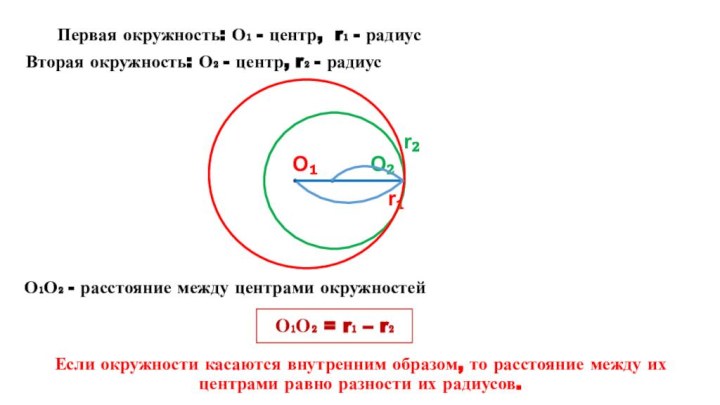
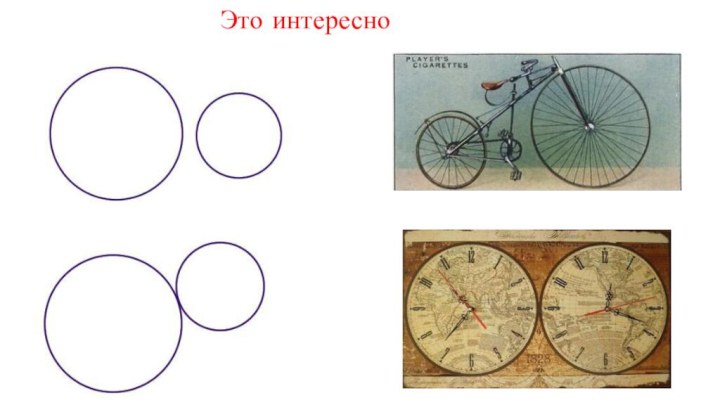
вам известны?
Повторение
Для каждого случая сравните радиус окружности расстояние от
центра окружности до прямойКакая прямая называется касательной?
Какая прямая называется секущей?
Как проходит касательная по отношению к радиусу окружности?