Презентация на тему Комбинаторика в ГИА

Путь размышлений - самый благородный, путь подражания - самый

лёгкий, путь опыта - самый горький".

Комбинаторика в ГИА

комбинаторных задач на ГИА
расширить математический кругозор
Шпаргалка и немного истории

навыков решения задач 2 части
Полезные ссылки

сферы мысли,
к которым можно отнести
все математические идеи.

Английский математик Джеймс Джозеф Сильвестр (1814-1897)

о том, сколько различных комбинаций, подчиненных тем или иным

условиям, можно составить из заданных объектов.

возможных вариантов или подсчета их числа.
ОРГАНИЗОВАННЫЙ ПЕРЕБОР –

строгий порядок разбора всех случаев,
возможных решений.

и вычислите
Р2 и Р4




3! = 1۰2۰3=6
Р4 = 4!=1۰2۰3۰4=24

вычислите

мы пользуемся:
А.сочетанием,
Б.перебором,
В.пересечением множеств.
2. Комбинаторика изучает:
А.деятельность

комбинатов бытового обслуживания,
Б.способы пошива комбинезонов,
В.способы решения задач на различные комбинации объектов.

в пункт В через пункт С, можно воспользоваться правилом:

А.сложения,
Б.умножения,
В.возведения в степень.
4. Для вычисления количества всевозможных пар вашей группы необходимо знать формулы:
А.сочетаний,
Б.сокращенного умножения,
В.теорему Пифагора.

Ответьте на вопросы теста

5,
Б.квадрат числа 5,
В.произведение натуральных чисел от 1

до 5 (вычислите).
6. Комбинаторные задачи встречаются в профессиональной деятельности:
А. парикмахера-визажиста,
Б. диспетчера автовокзала,
В. завуча школы,
Г. экономиста,
Д. повара
(добавьте свой пример)

Ответьте на вопросы теста

задаче;
значок Совы- шпаргалка)
Выписаны все трехзначные числа из цифр

0, 2, 4, 6 в порядке возрастания. Какое следует за 426?
2. В классе 15 девочек и 10 мальчиков. Сколькими способами можно выбрать для дежурства двоих: 1 девочку и 1 мальчика?
3. В расписании на среду 4 урока: математика, русский и 2 урока физкультуры. Сколькими способами можно составить расписание?
4. В коробке 4 шара: белый, синий, красный, зеленый. Из неё извлекают 2 шара Сколько различных комбинаций можно получить? Сколько вариантов вынуть 2 шара различного цвета?

визиткой. Сколько всего карточек понадобилось?
6. Сколько трехзначных чисел можно

записать, используя цифры 0, 2, 4, 6?
7. В чемпионате по футболу играет 10 команд. Сколькими способами могут распределиться три призовых места?

рукопожатиями. Сколько сделано рукопожатий?
2.(4) Из нечетных цифр составляют все

возможные числа, содержащие не более 4 цифр. Сколько существует таких чисел?
3.(4) Сколькими способами можно составить расписание на день , если должно быть 5 уроков: алгебра, геометрия, физика, биология, география, при этом алгебра и геометрия должны стоять рядом, а урок биологии обязательно первым?
4.(6) После матча каждый игрок одной команды обменялся рукопожатием с каждым игроком другой. Сколько игроков было всего на площадке, если рукопожатий было совершено 323?

Встретились несколько друзей и все обменялись рукопожатиями. Всего было

сделано 15 рукопожатий. Сколько встретилось друзей?
3) Придумайте как можно больше комбинаторных задач с использованием данных объектов: Четверо друзей: Катя, Олег, Света, Андрей.

Закрепление материала

Если первое действие можно выполнить n1 способами …, то

все k действий вместе могут быть выполнены n1 × n2× n3 × …× nk способами.
n! = 1×2 ×… ×n
Комбинации из n-элементов, отличающиеся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов Р = n!
Комбинации из n элементов по k , отличающиеся друг от друга лишь составом элементов, называются сочетаниями из n элементов по k. Количество сочетаний можно посчитать по формуле


Комбинации из n элементов по k, отличающиеся друг от друга либо
составом элементов, либо порядком их расположения, называются
размещениями из n элементов по k (k≤n).

В математике есть задачи, в которых требуется из элементов

составить различные наборы, подсчитать количество всевозможных комбинаций элементов, составленных по определённому правилу. На практике часто приходится делать перебор определённого количества данных. Например, учителю приходится распределять различные виды работ между группами учащихся, офицеру выбирать из солдат наряд, агроному размещать культуры на полях, завучу составлять расписание и т.д. В данном случае речь идёт о всевозможных комбинациях объектов. Задачи такого типа называются комбинаторными задачами. Область математики, в которой изучают комбинаторные задачи, называется комбинаторикой. Как самостоятельный раздел математики комбинаторика оформилась в Европе в XVIII веке. Некоторые комбинаторные задачи решали в Индии во II веке до н. э., в Древнем Китае, позднее в Римской империи.

Немного истории

введён в математический обиход знаменитым Лейбницем. Готфрид Вильгельм Лейбниц(1.07.1646

- 14.11.1716) - всемирно известный немецкий учёный, занимался философией, математикой, физикой, организовал Берлинскую академию наук и стал её первым президентом. В 1666 году Лейбниц опубликовал "Рассуждения о комбинаторном искусстве". В своём сочинении Лейбниц ввел специальные символы, термины для подмножеств и операций над ними. В течение всей своей жизни Лейбниц многократно возвращался к идеям комбинаторного искусства. Комбинаторику он понимал весьма широко, именно, как составляющую любого исследования, любого творческого акта, предполагающего сначала анализ (расчленение целого на части), а затем синтез (соединение частей в целое). Комбинаторике Лейбниц предрекал блестящее будущее, широкое применение. В XVIII веке к решению комбинаторных задач обращались выдающиеся математики.

Г.В. Лейбниц

о паросочетаниях, о циклических расстановках, о построении магических и

латинских квадратов. В 1713 году было опубликовано сочинение Я. Бернулли "Искусство предположений", в котором с достаточной полнотой были изложены известные к тому времени комбинаторные факты. Сочинение состояло из 4 частей, комбинаторике была посвящена вторая часть, в которой содержатся формулы. Для вывода формул автор использовал наиболее простые и наглядные методы, сопровождая их многочисленными таблицами и примерами. В работах Я. Бернулли и Лейбница тщательно изучены свойства сочетаний, размещений, перестановок.

возврат

Л. Эйлер

Я. Бернулли

увеличить нельзя. Можно увеличить разряд десятков с 2 до

4, единиц, тогда 0.

возврат

4

2

6

0

4

1 девочку можно выбрать 15 способами и 1 мальчика

– 10 способами. Пару девочка-мальчик - 15∙10=150 способами.

возврат

уроков, затем русский язык- на любой из трех оставшихся

, а для двух уроков физкультуры остается единственный вариант постановки в расписание.
По правилу умножения 4∙3=12

возврат

пар шаров:













возврат
Комбинации из 4 элементов по 2 , отличающиеся

друг от друга лишь составом элементов, называются сочетаниями из 4 элементов по 2. Количество сочетаний можно посчитать по формуле

29 визитных карточек.
Всего 29∙30=870 карточек.

возврат

кроме 0 – это 3 варианта, остальные цифры имеют

4 варианта. По правилу умножения
3∙4 ∙4=48.

возврат

10 команд, на второе – любую из 9 команд,

а на третье – любую из 8 оставшихся По правилу умножения, общее число способов 10∙9∙8=720.

возврат

Комбинации из 10 элементов по 3 , отличающиеся друг от друга либо составом элементов, либо порядком их расположения называются размещениями из 10 элементов по 3. Количество размещений можно посчитать по формуле

5 человек. На первое место можно поставить любого из

5, на второе – любого из 4. По правилу умножение 4∙5=20.Но порядок учитывать не нужно, то

возврат

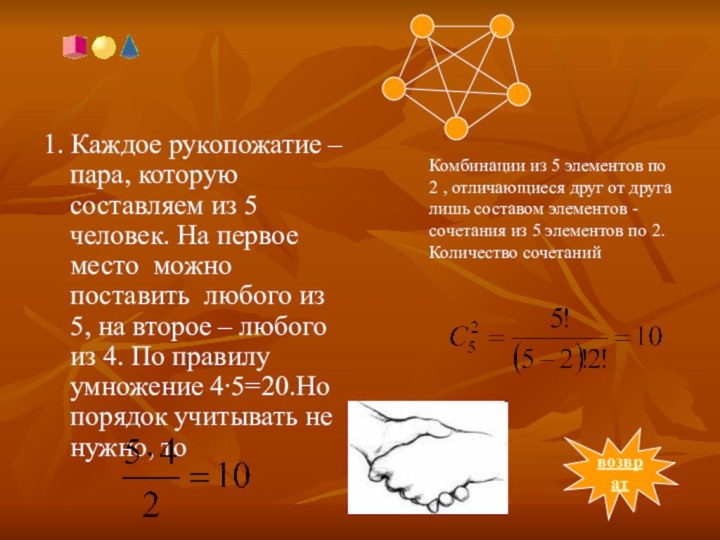
Комбинации из 5 элементов по 2 , отличающиеся друг от друга лишь составом элементов -сочетания из 5 элементов по 2. Количество сочетаний

- 5∙5=25
Трехзначных – 125, четырехзначных - 625
Всего 5+25+125+625=780.


возврат
5
5

уроков алгебры и геометрии возможны
3 варианта расположения в

расписании, при этом в
2-х комбинациях(алгебра-геометрия, геометрия-алгебра).
Физику на любое место из двух оставшихся,
географию на последнее оставшееся.
По правилу
умножения 3∙2∙2 1=12.
Ответ: 12.

M игроков. N и M – целые числа. По

правилу умножения
было совершено N⋅M рукопожатий. Т.е. N⋅M=323- уравнение в целых числах. Варианты разложения на два множителя :
1⋅323=323 и 17⋅19=323
То значения N=1; 17; 19.
В хоккейной команде не может быть 1 человек.
Следовательно в командах по 17 и 19 человек соответственно, их сумма 17+19=36.
Ответ: 36 человек

возврат