Слайд 2
«Мы слишком часто даем детям ответы, которые надо
выучить,
а не ставим перед ними проблемы, которые надо
решить».
Роджер Левин
Федеральный государственный образовательный стандарт определил приоритетные направления развития образования. Одно из них - МЕТАПРЕДМЕТНЫЙ ПОДХОД, как средство достижения метапредметного результата.
Слайд 3
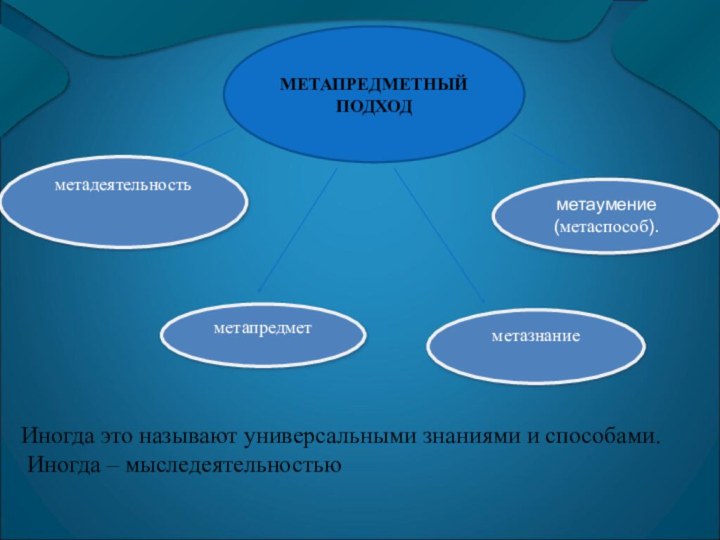
метадеятельность
метаумение (метаспособ).
метазнание
метапредмет
МЕТАПРЕДМЕТНЫЙ
ПОДХОД
Иногда это называют универсальными знаниями и способами.
Иногда –
мыследеятельностью
Слайд 4
МЕТАПРЕДМЕТНЫЙ ПОДХОД
(ГРОМЫКО Н. В. кандидат философских наук,
зам. директора Института инновационных стратегий развития общего образования при
Департаменте образования г. Москвы)
МЕТАЗАДАЧА
МЕТАЗНАК
МЕТАЗНАНИЕ
МЕТАПРОБЛЕМА
Слайд 5
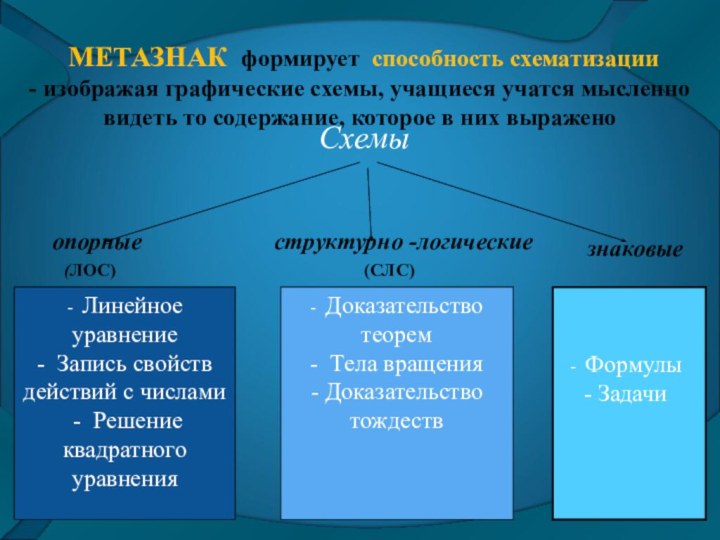
МЕТАЗНАК формирует способность схематизации
- изображая графические
схемы, учащиеся учатся мысленно видеть то содержание, которое в
них выражено
- Линейное уравнение
- Запись свойств действий с числами
- Решение квадратного уравнения
- Доказательство теорем
- Тела вращения
- Доказательство тождеств
Схемы
опорные структурно -логические
Формулы
Задачи
(ЛОС)
(СЛС)
знаковые
Слайд 6
«МЕТАЗАДАЧА»
Формируются способности :
-понимания и схематизации условий;
-моделирования объекта задачи;
-конструирования
способов решения;
-выстраивания деятельностных процедур достижения цели.
Тип
философствования учащихся связан:
с процессом постановки задач, поиском и рефлексией средств их решения;
с освоением техник перевода проблем в задачи и т. д.
С помощью метазадач на уроках математики учащиеся получают знание о разных типах задач и способах их решения (задачи на движение, на работу, статистики и д.р.)
Слайд 7
МЕТАПРОБЛЕМА
- предполагает понимание разных профессиональных языков, умение
ориентироваться в разных областях практической деятельности
Работая над МЕТАПРОБЛЕМОЙ, школьники
учатся обсуждать вопросы, которые носят характер открытых, по сей день неразрешимых проблем, тем самым осваивают технологии позиционного анализа, отрабатывают умение организовывать и вести диалог, развивают способности целеполагания, самоопределения.
Слайд 8
Математика 6 класс, тема «Сравнение чисел»
После проверки
домашнего задания проводится устная работа.
1) Назвать число, противоположное данному,
провожув форме игры « Ты – мне, я – тебе »
45; 6; -8; 0 и т.д.
2) Найти модуль числа 4,5; -48; 19; 0 и т.д.
3) Выбрать число, имеющее больший модуль:
-5,87 и -7,82; -2,75 и 0; -5/8 и 5/9;
700,1 и 0,24; -0,5 и -1/2; -2 и 3 .
4) Между какими двумя целыми числами на координатной прямой расположено данное число:
4; 2,73; 0; -9; -1 .
Слайд 9
Обычно на последних заданиях ребята затрудняются дать правильный
ответ и догадываются немногие учащиеся.
Ставиться проблема: как сравнить отрицательные
числа, можно ли сравнивать эти числа без обращения к координатной прямой?
Слайд 10
Даю ребятам такие задания: Какое число на координатной
прямой лежит левее?
2 или
-1; -4 или -6; -3 или 0; -7 или -9.
Какое число на координатной прямой лежит правее?
7 или -2; -1 или -5; 0 или -6; 2 или -4.
№ 958. Запишите результаты в виде неравенств и сделайте выводы: как можно сравнить положительные и отрицательные числа без использования координатной прямой?
а) 0 и 3; б) 0 и -5; в) 8 и 0; г) -7 0; д) -2 3; е) -7 1; ж) 1 -10; з) 3 -3; и) 1 8; к) -5 -3; л) -5 -10; м) -2 -5.
Слайд 11
Взаимопроверка на местах. После этого раздаю
учащимся листочки с предложениями, в которые они вставляют пропущенные
слова:
- Любое положительное число больше нуля
- Любое положительное число больше любого отрицательного числа
- Любое отрицательное число меньше нуля
- Любое отрицательное число меньше любого положительного числа
- Из двух отрицательных чисел больше то, модуль которого меньше, а меньше то, модуль которого больше.
Слайд 12
Ещё раз обговариваем составленные правила, я обращаю внимание
учащихся на связь слов:
отрицательное число – левее нуля –
со знаком минус – меньше нуля; пишут: а < 0
положительное число – правее нуля – со знаком плюс – больше нуля; пишут: a > 0.
Таким образом, наша проблема решена.
Слайд 13
Математика 6 класс. Тема «Длина окружности и площадь
круга»
на каждую парту я раздаю разные геометрические фигуры( треугольники
–разносторонний, равносторонний, прямоугольный; квадрат, прямоугольник, трапеция, ромб, круги разных диаметров к которым прикреплены нитки) и прошу ребят найти среди них те фигуры площадь которых они умеют вычислять. Как правило, ребята всегда откладывают прямоугольник и квадрат.
Слайд 14
- Площадь какой фигуры ещё можно найти с
помощью прямоугольника? Ответ: прямоугольного треугольника.
- Вспомним и запишем
формулы для вычисления площадей этих фигур.
(записываем на доске и в тетрадях).
S =ab; S= a2; S=ab/2
Слайд 15
сегодня мы узнаем как вычисляется площадь круга и
длина окружности.
Возьмите в руки круг (по вариантам даны разные
круги радиус 3см и 4,5 см)
Посмотрите внимательно на фигуру и выполните следующие задания.
Отметьте центр окружности О. Проведите диаметр АВ.
Можно ли ещё провести диаметры? Чем является отрезок ОВ?
Есть ли еще радиусы? Сколько радиусов и диаметров в окружности?
Какой отрезок называется хордой?
Что можно сказать про диаметры?
Слайд 16
Можно ли измерить хорду, радиус?
Что еще можно
измерить у фигуры ( Длину окружности.)
Какую геометрическую
фигуру ограничивает окружность? (Круг.)
Что еще можно вычислить? ( Площадь круга.)
Как вы думаете, ребята, удобно ли измерять окружность с помощью линейки? А можно это сделать?(нет, линейка сломается) Ставится проблема: Как же нам измерить длину окружности? (Так как к кругу прикреплена нить, то дети догадываются, что нужно измерить этой нитью)
Давайте измерим окружность нитью, а затем узнаем её длину, приложив к линейке.( по вариантам)
Слайд 17
Запишите найденное значение в тетради: С=…
Это число математики
обозначали буквой π (пи).
π = 3,141592653589793238462643… (24 знака).
π =3,14.
Используя найденное нами число, мы получаем формулы
С= πd или С = 2πr.
Слайд 18
Решаем задачу
У меня на участке есть клумба
в форме круга,
диаметр её 2,4 м. Она оформлена
дощечками.
Длина одной дощечки 6 см.
Сколько мне нужно дощечек,
чтобы огородить всю клумбу?
Какую площадь моего участка занимает клумба?
Слайд 19
Алгебра 9 класс. Тема «Сумма n- первых членов
арифметической прогрессии»
Уже с 7 – го класса ребятам хорошо
владеющих математикой я даю задания на нахождении суммы нескольких натуральных слагаемых.
Найдите сумму первых 10-ти натуральных чисел; первых 20 – ти натуральных чисел и т.д. В 9 классе изучение вопроса о сумме n–первых членах арифметической прогрессии начинаю с рассказа о маленьком немецком ученике Карле Фридрихе Гаусс . Как удалось Гауссу так быстро подсчитать сумму 100 первых натуральных чисел?”
Слайд 20
Проблемная ситуация: как найти быстро сумму первых 100
натуральных чисел?
Обязательно, кто-нибудь из учеников вспоминает задания младших классов
и предлагает решение проблемы
(1 + 100) х 50 = 5050.
Теперь выводим формулу суммы n-первых членов арифметической прогрессии.
Слайд 21
Математика 5 класс. Тема «Проценты»
Начинаю урок с чтения
из газет, журналов предложений, содержащих проценты; спрашиваю ребят, как
они понимают такие записи. Рассказываю ребятам, что все классные руководители в конце триместра подсчитывают качество знаний своего класса. Помогите мне узнать качество знаний вашего класса. Дети говорят, что они не могут помочь, так как не знают, что такое процент. Проблемная ситуация создана. Даём определение процента и решаем различные практические задачи.
Слайд 22
Группа учащихся увлеклась проектом «Математические задачи в
жизни человека». Они исследовали задачи ЕГЭ В1, брали интервью
у своих родителей, медиков, продавцов, водителей, директора школы, поваров, задавая им вопрос «Пригодилась ли им математика в жизни? Решают ли взрослые в своей жизни математические задачи?» Подготовили отличную презентацию и выпустили книгу для 11 класса «Задачи ЕГЭ В1».
Слайд 24
Геометрия 7 класс. Тема «Сумма углов треугольника»
Даю задание
учащимся: построить с помощью транспортира треугольник по его углам
для 1 варианта: 90°, 35° и 50°, для 2 варианта: 80°, 40° и 25°.
Ребята не могут построить такие треугольники. Возникает проблема «Почему нельзя построить треугольник, ведь известны все его углы?» Возникает потребность в изучении теоремы.
Слайд 25
В нашем селе в основном занимаются выращиванием бахчевых
культур и турецкая национальность выращивает овощи. Поэтому, работая над
МЕТАПРОБЛЕМОЙ, мы с учащимися на уроках математики обсуждаем вопросы, которые носят характер нужный, практически каждый день, например “ Сколько краски надо для ремонта дома. Сколько купить плёнки для строительства парника, сколько нужно семян перца, чтобы засеять 2 гектара земли и т.д.”, тем самым осваивают технологии позиционного анализа, отрабатываются умения организовывать и вести диалог, развиваются способности целеполагания, самоопределения.
Слайд 26
Проект «Прямоугольный параллелепипед. Площадь его поверхности»
поставлена проблема: Помочь
своим родителям и выяснить, сколько банок краски весом 2
кг нужно для ремонта вашего класса (кабинет географии), если 1банка расходуется на 4 квадратных метра.
Слайд 27
На своих уроках я провожу различные игры
: поле чудес, своя игра, умники и умницы, математические
марафоны, викторины.
Игры ставят ученика в условия поиска, пробуждают интерес к победе.
Слайд 28
Заключение
Уроки проблемного изложения материала позволяют реализовать метапредметный подход
в обучении и отражают требования современного урока. Учащиеся становятся
активными участниками получения нового знания, развивается их самостоятельность, аналитическое и творческое мышления, развивается познавательная активность, появляется осознанности знаний, обеспечивается более прочное усвоение знаний, делает учебную деятельность более привлекательной для учащихся, ориентирует их на комплексное использование знаний.
Слайд 29
Литература:
-В.В. Выговская. Поурочные разработки по математике. 6 класс.
Москва. ВАКО.2008г
-Громыко Ю.В. Метапредмет «Проблема»/ Учебное пособие для учащихся
старших классов.- М.,1998.
- Глазунова О.С. Метапредметный подход. Что это?//Учительская газета 2011. № 9 [Электронный ресурс].-Режим доступа: http://www.ug.ru/article/64
- Громыко Ю. В. Мыследеятельностная педагогика (теоретико-практическое руководство по освоению высших образцов педагогического искусства). — Минск, 2000



























![Формирование метапредметных умений на уроках математики. [2010].URL: http://eidos.ru/shop/ebooks/220706/index.htm.-М.В.Величко .Математика.9-11 классы; Проектная деятельность учащихся.- Волгоград :Учитель, 2007-Л.И. Гриценко Педагогика](/img/tmb/6/581412/d2b6fc9a418112229af3e5d57834ce30-720x.jpg)