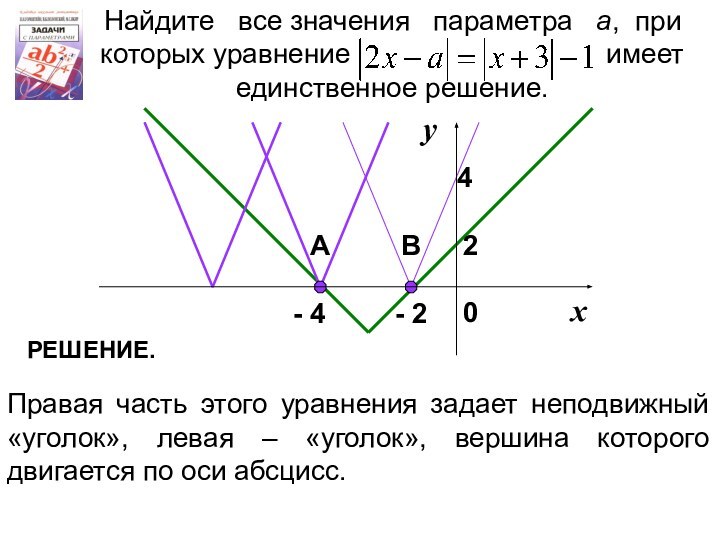
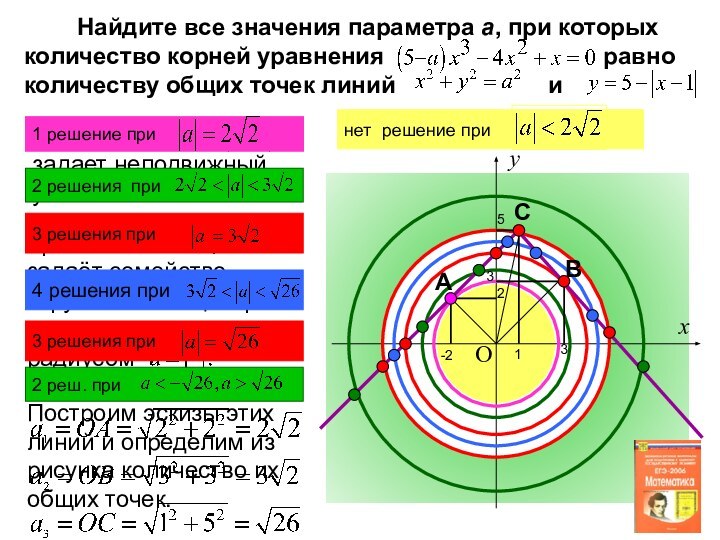
при которых уравнение
имеет единственное решение.Правая часть этого уравнения задает неподвижный «уголок», левая – «уголок», вершина которого двигается по оси абсцисс.
2
А
В
РЕШЕНИЕ.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть

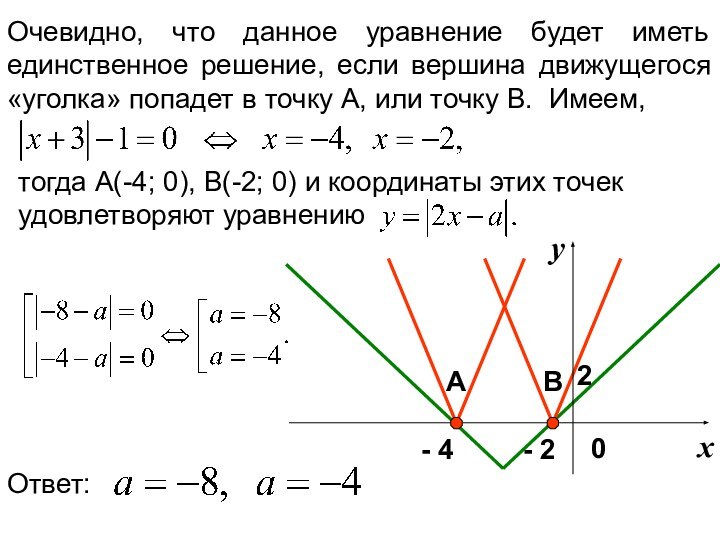





Правая часть этого уравнения задает неподвижный «уголок», левая – «уголок», вершина которого двигается по оси абсцисс.
2
А
В
РЕШЕНИЕ.
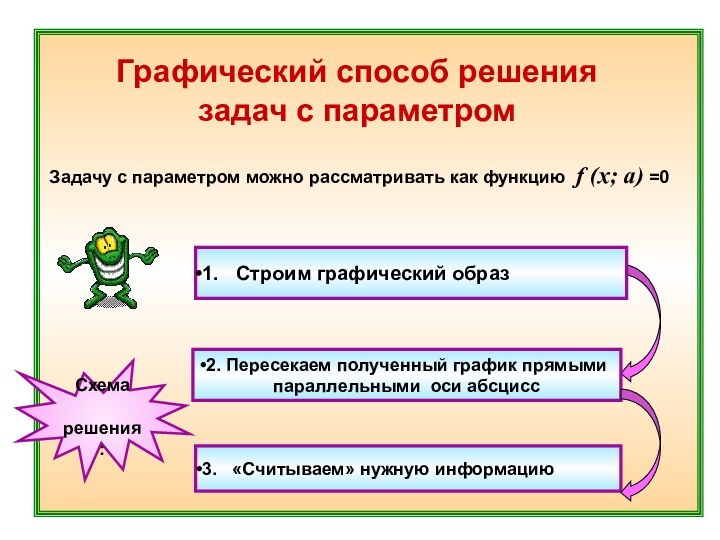
2. Пересекаем полученный график прямыми
параллельными оси абсцисс
3. «Считываем» нужную информацию
Схема
решения:
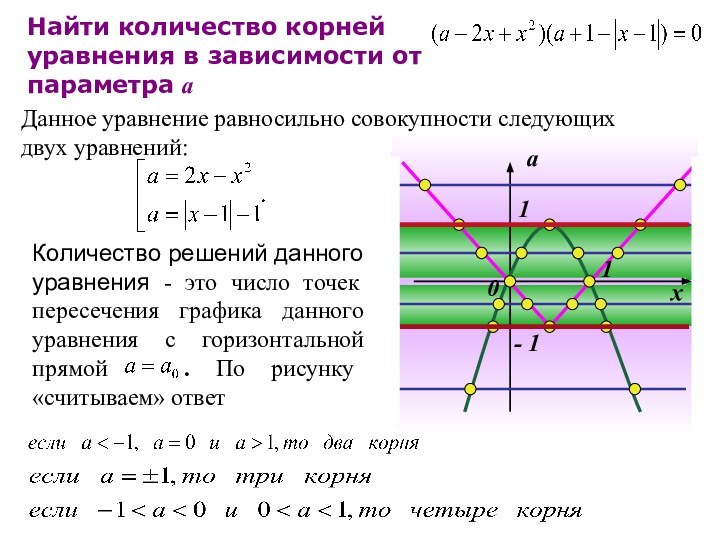
х
а
0
- 1
1
Найти количество корней уравнения в зависимости от параметра а
1
1.ОДЗ
2. Корни
3. Ось
4. Знаки на
интервалах
5. Ответ.
Метод интервалов:
Метод областей:
ОБОБЩЕННЫЙ МЕТОД ОБЛАСТЕЙ
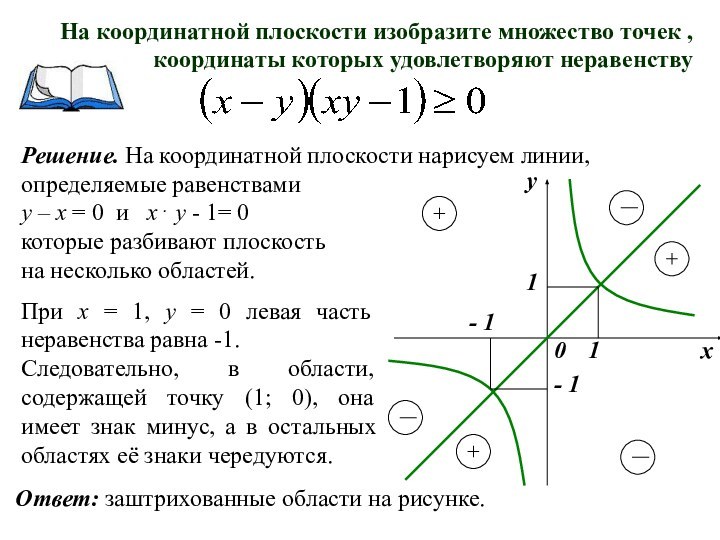
При х = 1, у = 0 левая часть неравенства равна -1.
Следовательно, в области, содержащей точку (1; 0), она имеет знак минус, а в остальных областях её знаки чередуются.
Ответ: заштрихованные области на рисунке.
х
у
0
1
- 1
- 1
1
На координатной плоскости изобразите множество точек , координаты которых удовлетворяют неравенству
- 1
- 1
1
1
х
у
0
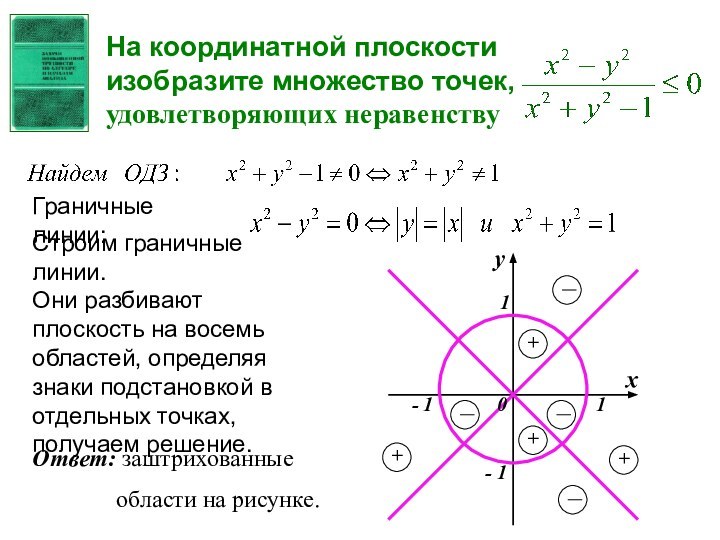
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству
Ответ: заштрихованные
области на рисунке.
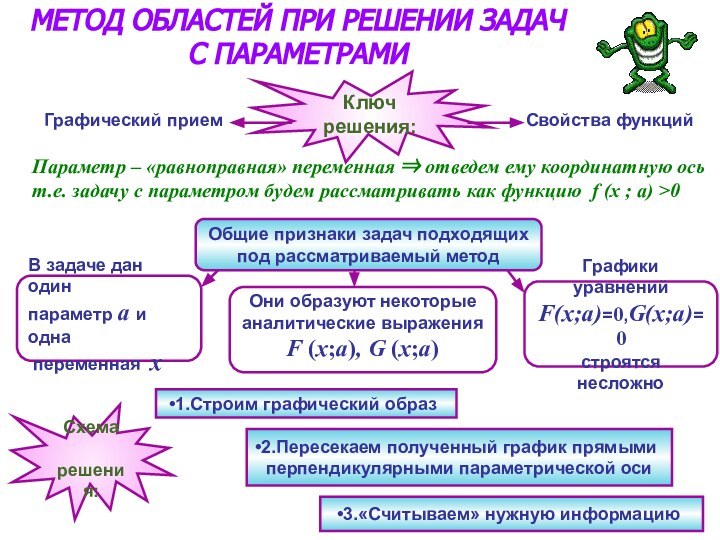
Общие признаки задач подходящих
под рассматриваемый метод
В задаче дан один
параметр а и одна
переменная х
Они образуют некоторые
аналитические выражения
F (x;a), G (x;a)
Графики уравнений
F(x;a)=0,G(x;a)=0
строятся несложно
1.Строим графический образ
2.Пересекаем полученный график прямыми
перпендикулярными параметрической оси
3.«Считываем» нужную информацию
Схема
решения:
.
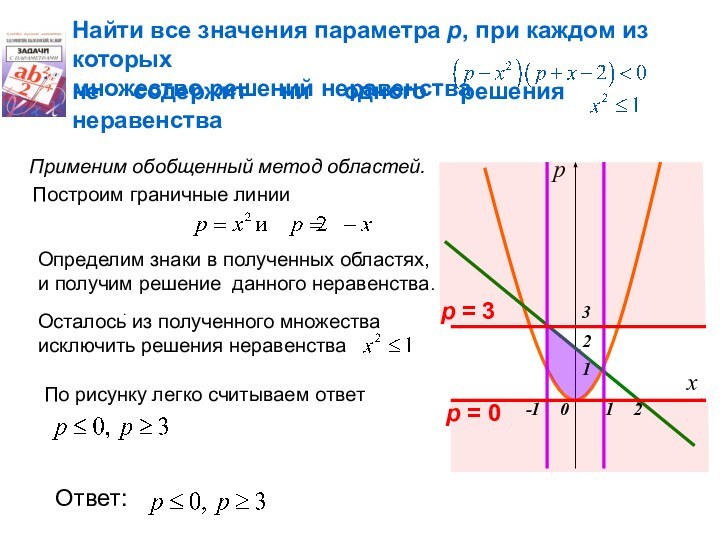
Применим обобщенный метод областей.
Определим знаки в полученных областях,
и получим решение данного неравенства.
По рисунку легко считываем ответ
Ответ:
Построим граничные линии
р = 3
р = 0
0
2
2
-1
1
3
1
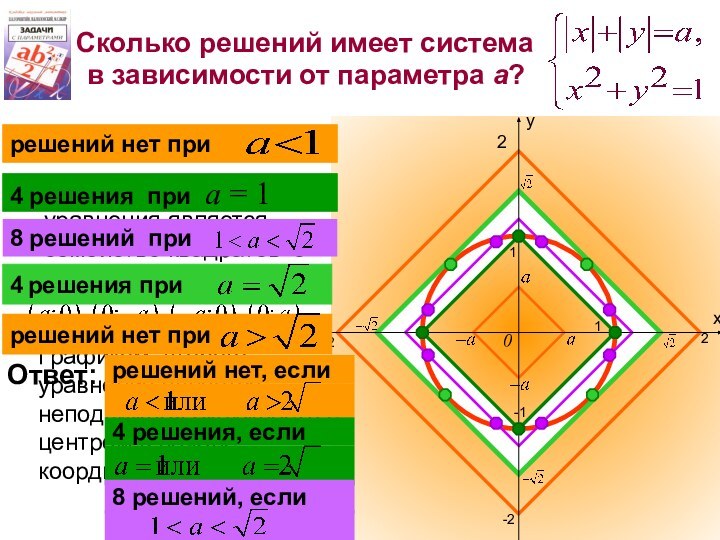
4 решения при а = 1
Ответ:
решений нет, если
8 решений, если
4 решения, если
0
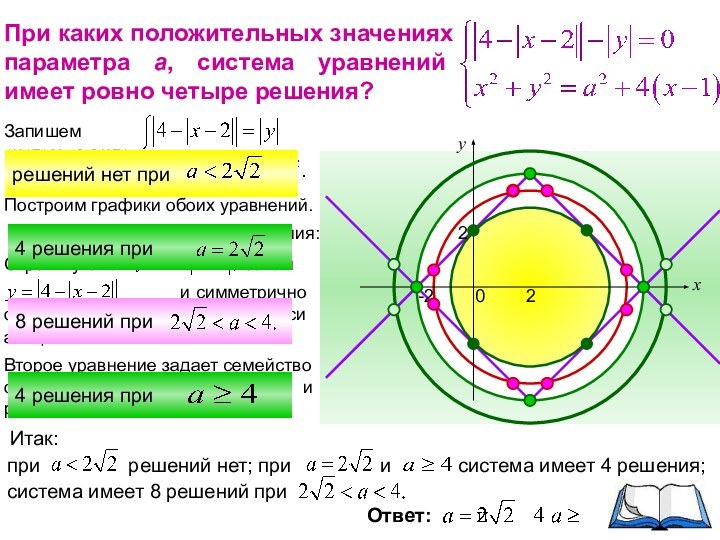
Второе уравнение задает семейство окружностей с центром (2;0) и радиусом а.
0
Ответ: a ∈ [5;12]
При каких значениях параметра а сумма и равна 1 хотя бы при одном значении х?
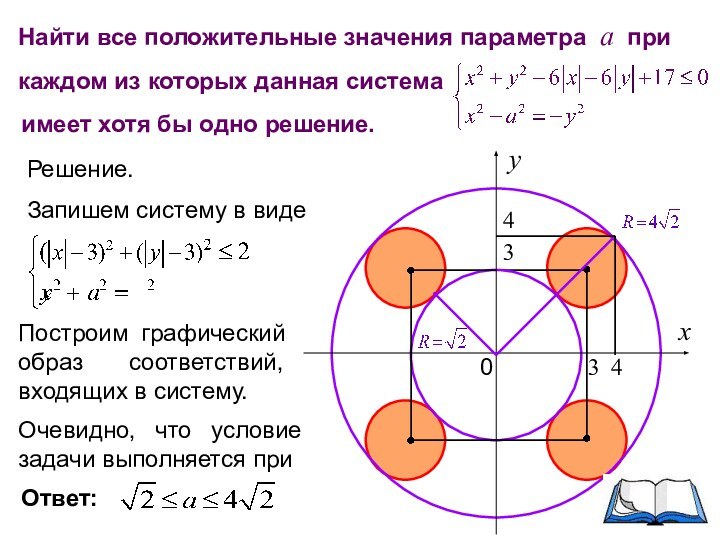
Решение.
Запишем систему в виде
Построим графический образ соответствий, входящих в систему.
3
3
4
4
Очевидно, что условие задачи выполняется при
Ответ:
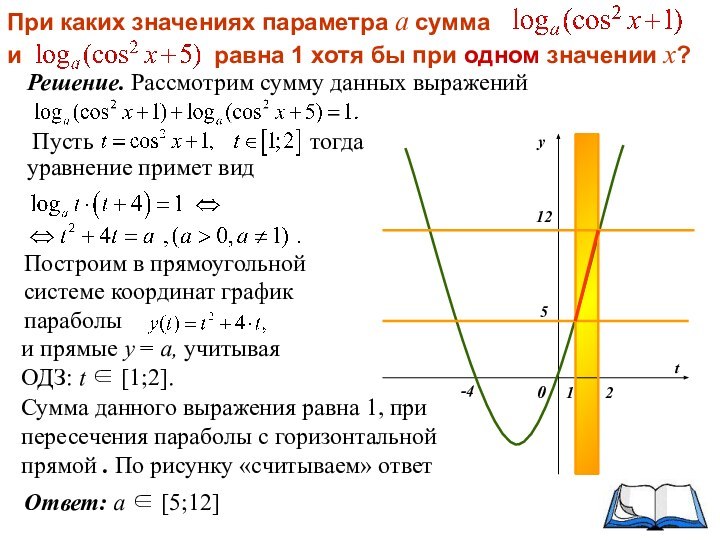
Введем новую переменную
тогда уравнение примет вид:
График левой части – парабола f (t), график правой части – прямая g(t).
3
2
-4
1
Решим задачу при условии равенства данных выражений.
Значит условие исходной задачи выполняется при