треугольника до его катета, равного 12, если
гипотенуза равна 15.Что требуется найти в задаче?
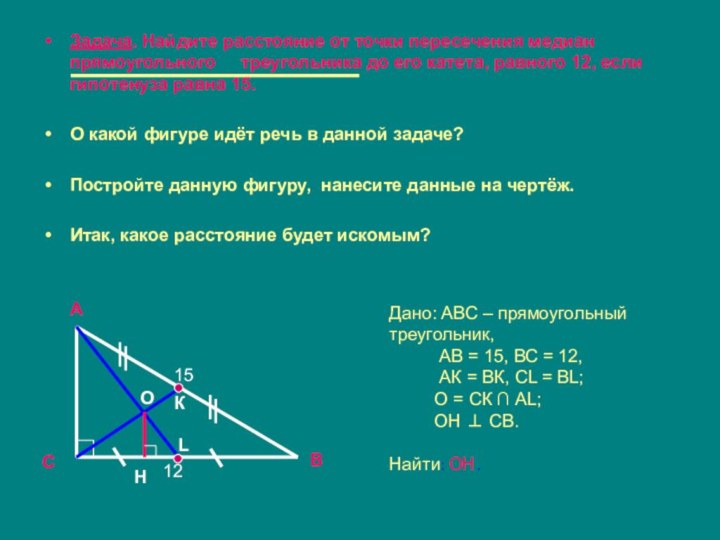
Расстояние от точки пересечения медиан до катета, равного 12, т.е. ОН.
Что мы сразу можем найти по данным задачи?
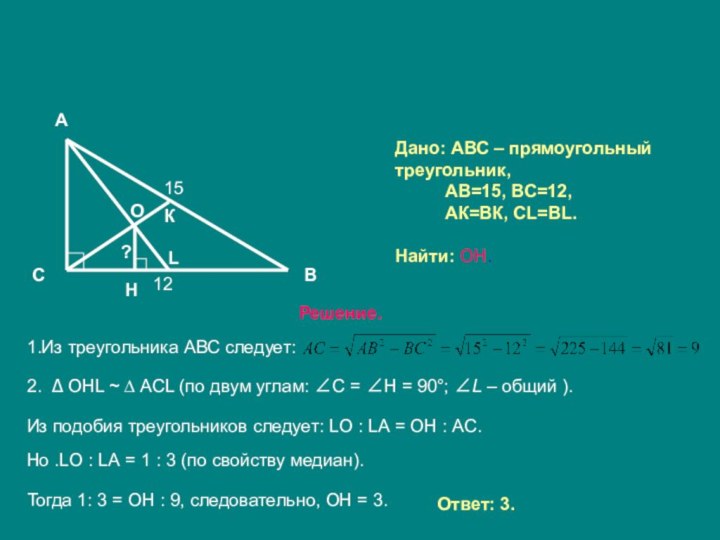
Из теоремы Пифагора второй катет.
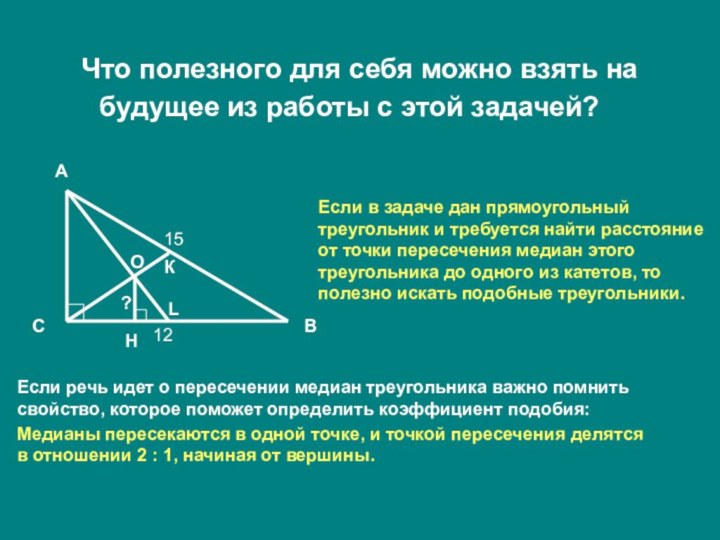
Что мы знаем о точке пересечения медиан треугольника?
Медианы пересекаются в одной точке, и точкой пересечения делятся в отношении 2:1, начиная от вершины.
Из какой фигуры мы можем найти искомое расстояние?
Из прямоугольного треугольника ОНL.
Как данная фигура связана с другими фигурами?
Треугольник ОНL подобен треугольнику АСL.
А
?
9
2к
1к
Что следует из подобия треугольников?
Равенство отношений соответствующих сторон.
Отношение каких сторон мы возьмём?
LО : LА = ОН : АС
Чему равно отношение LО : LА?
LО : LА = 1/3.
Составим план решения задачи.
1.Находим катет АС.
2.Рассматриваем подобные треугольники: ∆ ОНL и ∆ АСL.