- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по геометрии Теорема Пифагора (методический материал для недели математики)
Содержание
- 2. Пифагоровы штаны на все стороны равны
- 3. Так кто же такой Пифагор ?Пифагор-один из
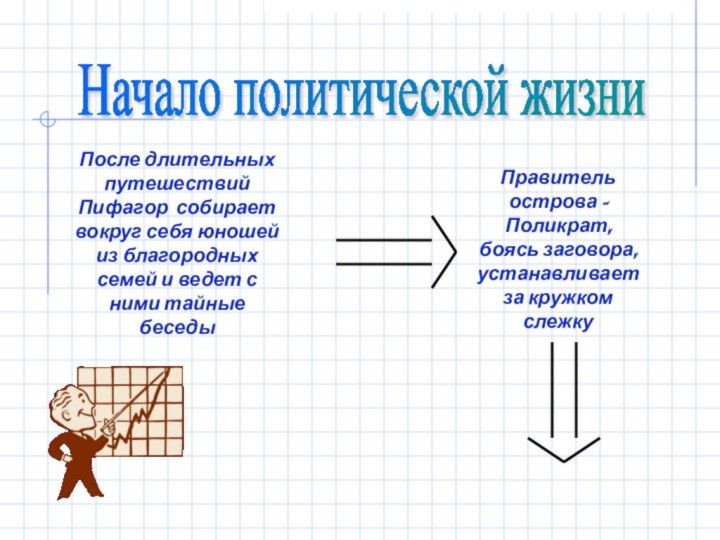
- 4. Начало политической жизни После длительных путешествий Пифагор
- 5. Правитель острова – Поликрат, боясь заговора, устанавливает
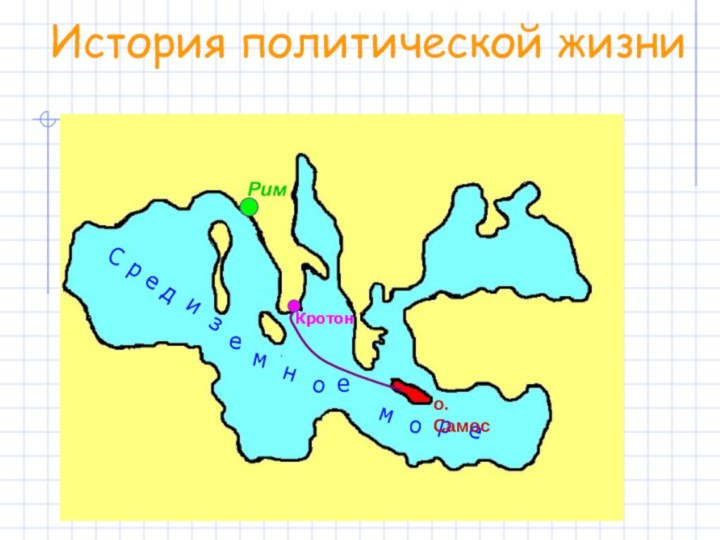
- 6. Римо.СамосКротонИстория политической жизни
- 7. Начало политической жизни Приехав в Кротон, Пифагор
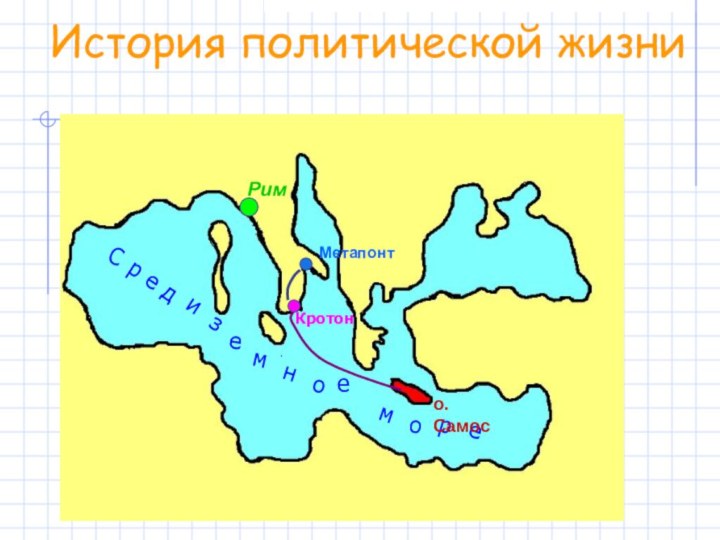
- 8. МетапонтИстория политической жизни
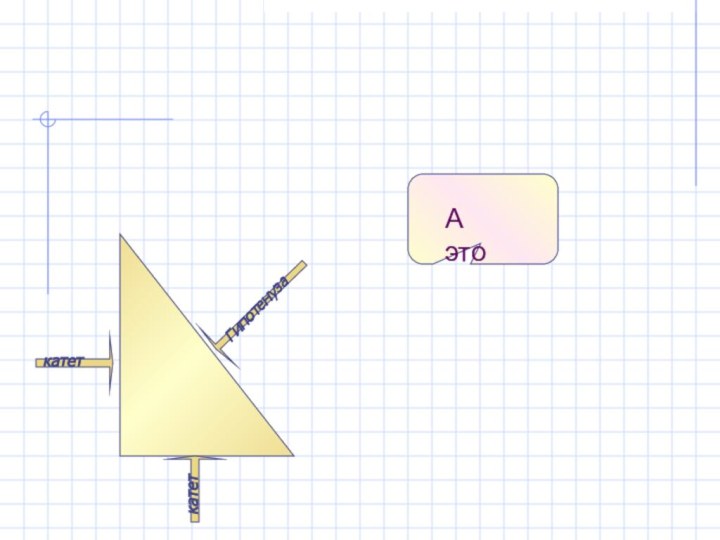
- 9. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.а2 + в2 = с2теорема
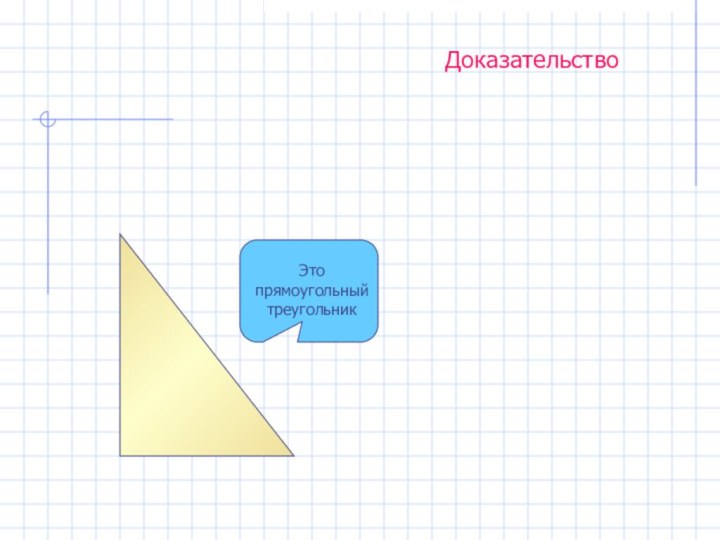
- 10. Доказательство Теоремы Пифагора Способ первый
- 11. Доказательство
- 12. А это
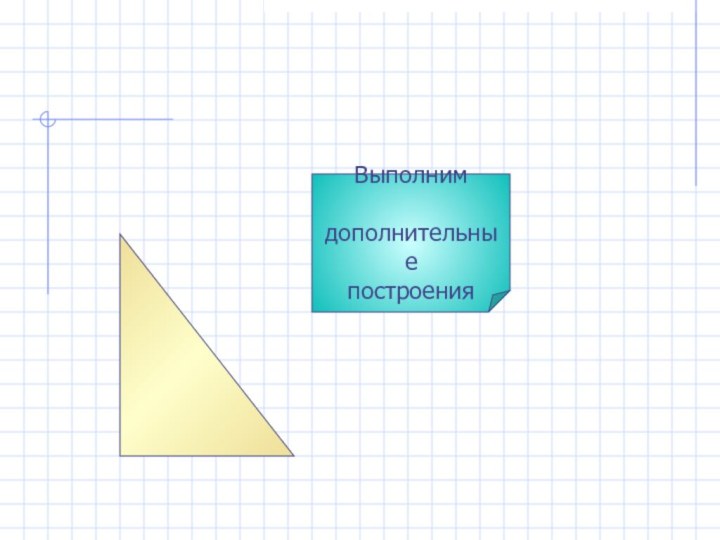
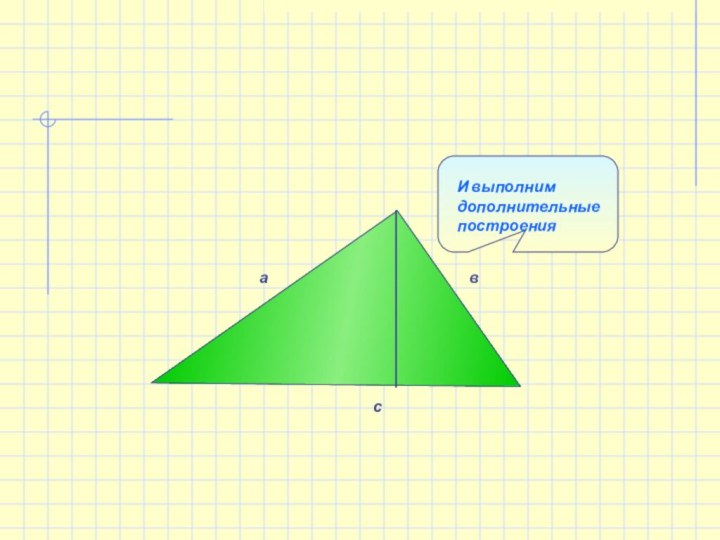
- 13. Выполним дополнительные построения
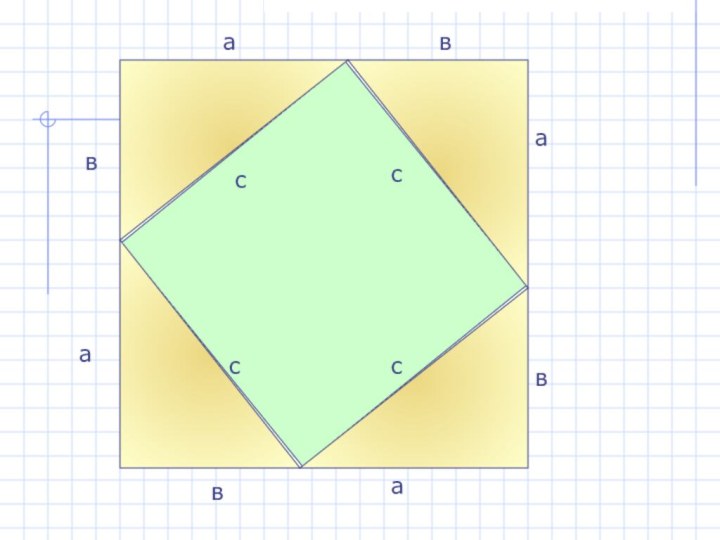
- 14. aвавававсссс
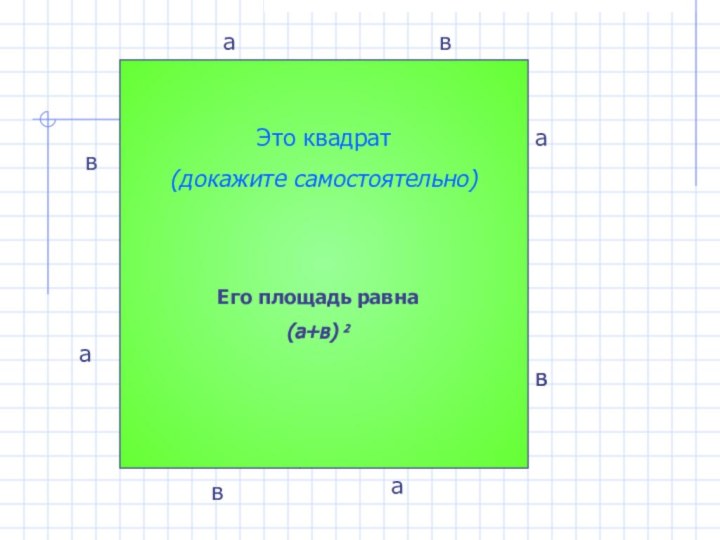
- 15. вaвавававссссссссЕго площадь равна(а+в) 2Это квадрат(докажите самостоятельно)
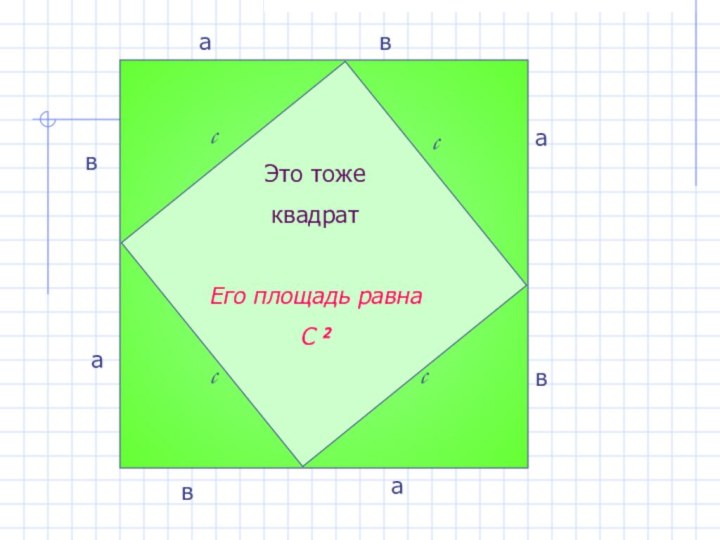
- 16. Это тоже квадратЕго площадь равнаС 2аввававаcccc
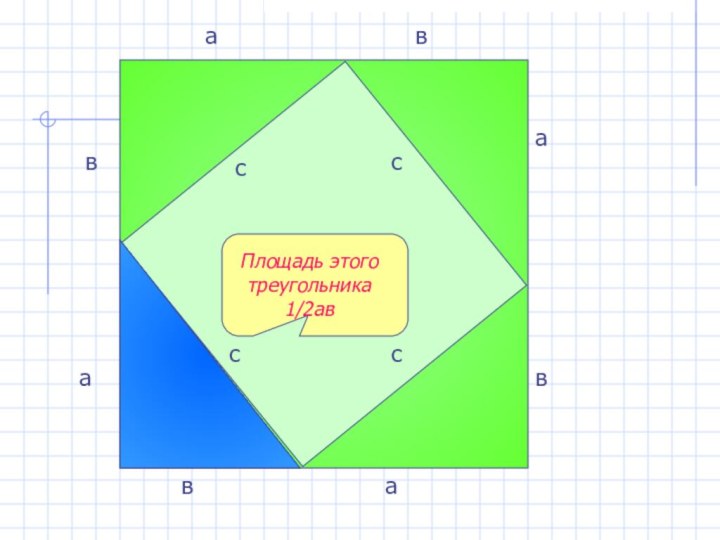
- 17. ссссПлощадь этого треугольника 1/2ававваваав
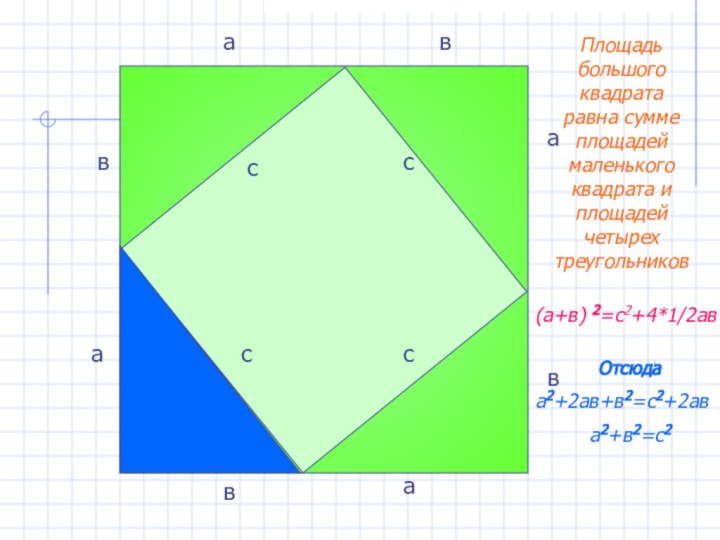
- 18. aвПлощадь большого квадрата равна сумме площадей маленького квадрата и площадей четырех треугольников(а+в) 2=с2+4*1/2ав Отсюдаа2+2ав+в2=с2+2ава2+в2=с2ававав
- 19. Доказательство Теоремы Пифагора Способ второй
- 20. Снова возьмем прямоугольный треугольник,площадь которого S
- 21. савИ выполним дополнительные построения
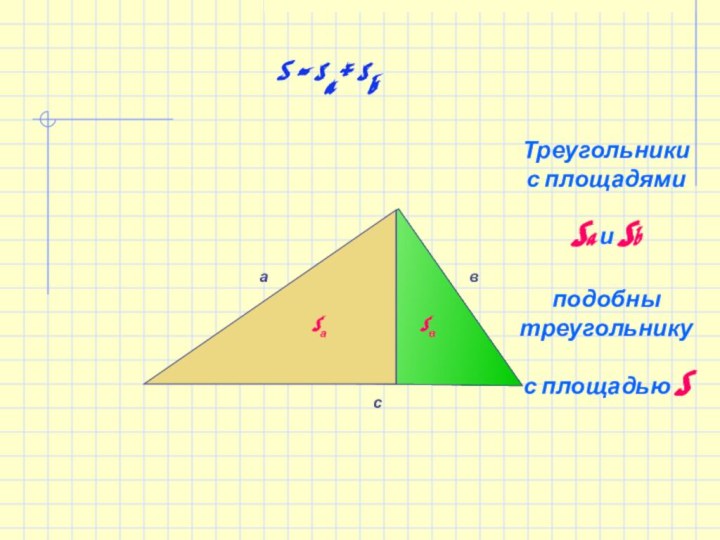
- 22. сsвS = sa + sbТреугольники с площадями sa и sb подобны треугольнику с площадью s
- 23. сsвСтороны первоначального треугольника - гипотенузы трех новых
- 24. Доказательство Теоремы Пифагора Способ третий
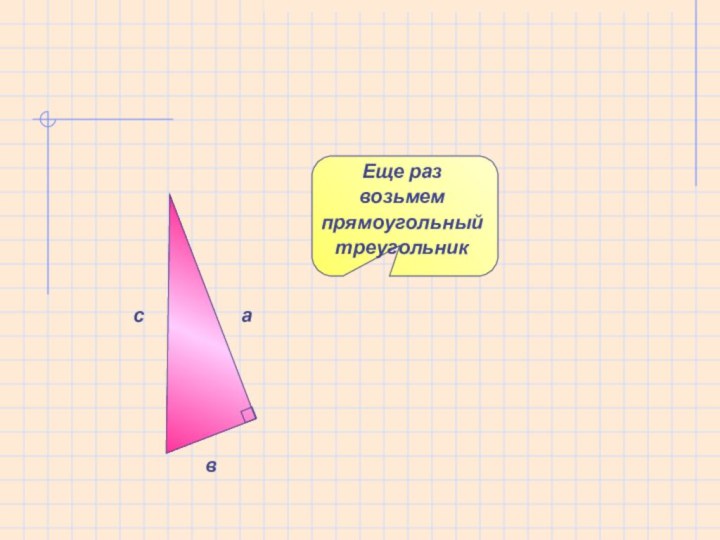
- 25. Еще раз возьмем прямоугольный треугольник
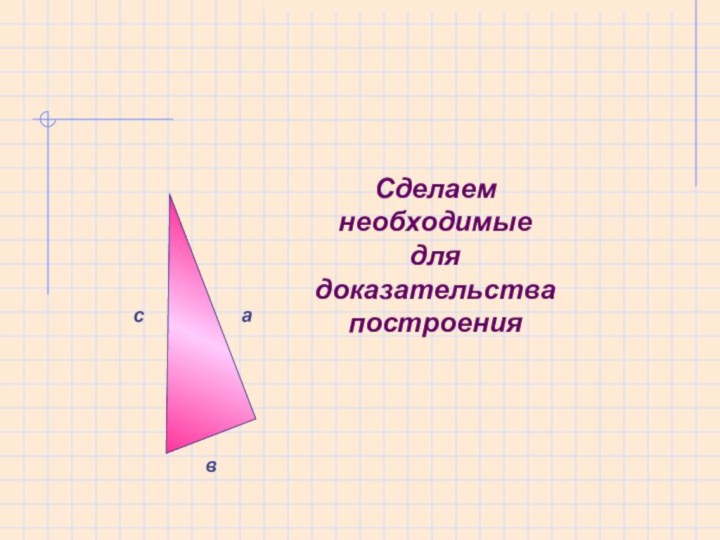
- 26. асвСделаем необходимые для доказательства построения
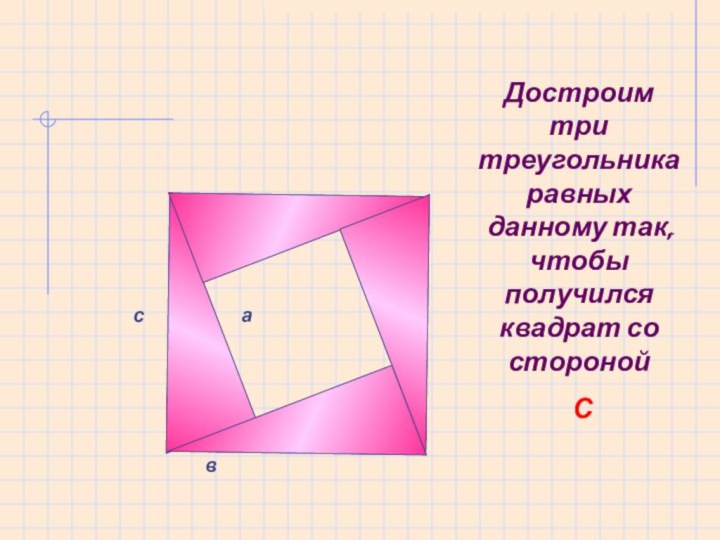
- 27. асвДостроим три треугольника равных данному так, чтобы получился квадрат со стороной С
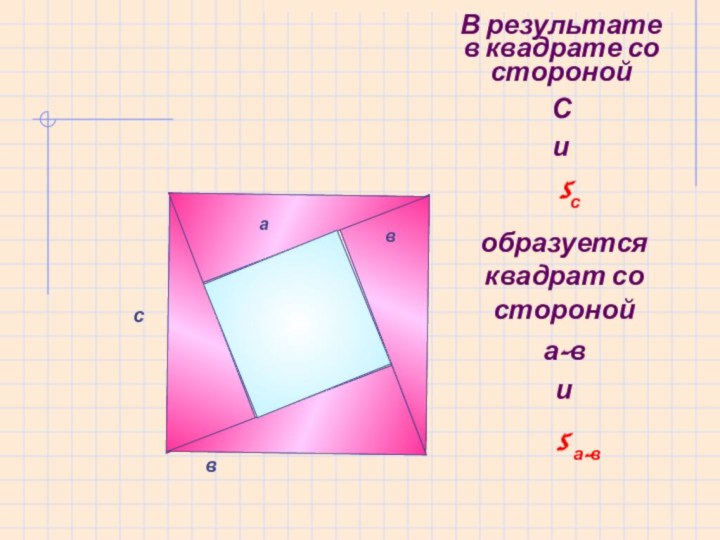
- 28. В результате в квадрате со стороной С иасвавSс образуется квадрат со стороной а-в и S а-в
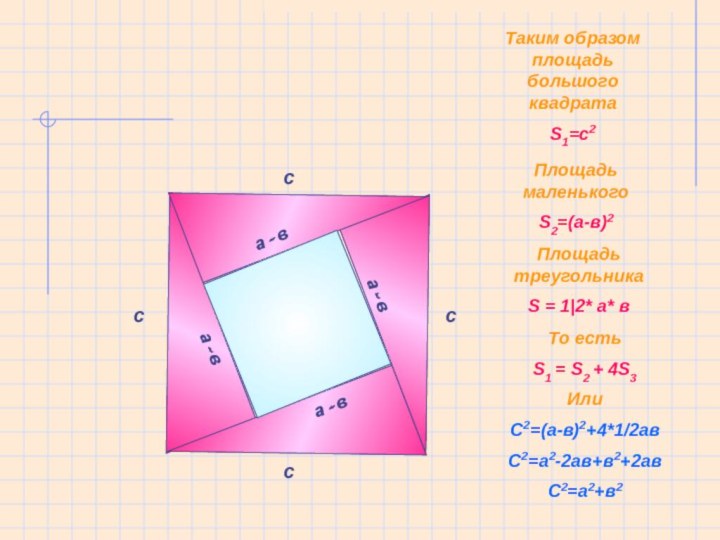
- 29. аТаким образом площадь большого квадрата S1=c2Площадь маленькогоS2=(а-в)2Площадь
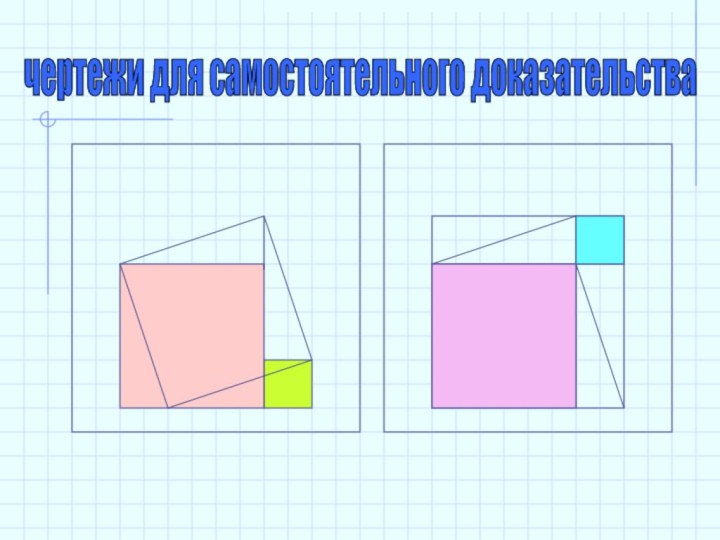
- 30. чертежи для самостоятельного доказательства
- 31. Прибудет вечной истина, коль скороЕё познает слабый
- 32. Скачать презентацию
- 33. Похожие презентации
Пифагоровы штаны на все стороны равны