приумножать их – мудрость, а умело применять – великое
искусство»(восточная мудрость)
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











![Тригонометрия 2cos3х + 4 sin(х/2) = 7Укажите число корней уравнения на промежутке [0; 2π]:sinх = ?](/img/tmb/14/1382528/eb56424f2eeec2dc6a857d2d6030c551-720x.jpg)


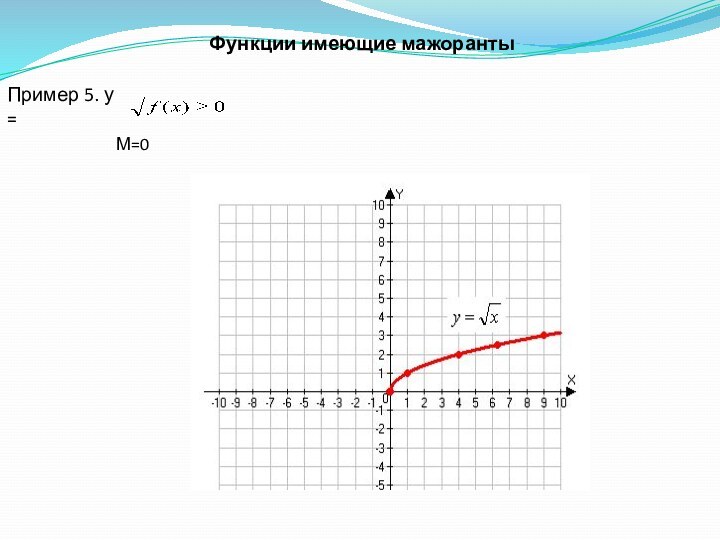




где
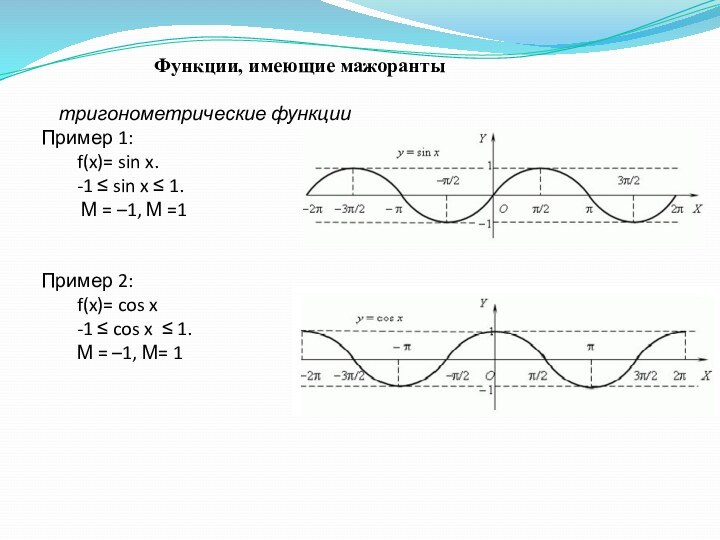
Пример 2:
f(x)= cos x
-1 ≤ cos x ≤ 1.
М = –1, М= 1
- верно
Ответ: