- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к открытому уроку по математике на тему Золотое сечение (6 класс)
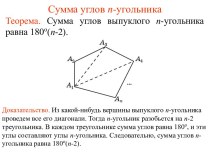
Содержание
- 2. Одно из самых удивительных явлений и открытий в математике. Что это?
- 3. Золотое сечениеЧто такое отношение?Отношение – другое название
- 4. Посчитаем?1. Разделим длину меньшей части отрезка на
- 5. Золотое сечениеЗолотое сечение – такое пропорциональное деление
- 6. Парфенон
- 7. В архитектуреХрам Василия Блаженного
- 8. В СкульптуреСтатуя Зевса
- 9. В ЖивописиМона Лиза (Джоконда)
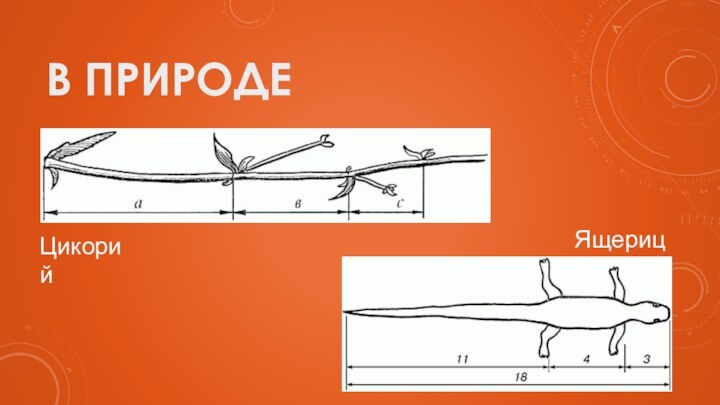
- 10. В ПриродеЦикорийЯщерица
- 11. ПостроениеНачертим отрезок любой длины и назовем его
- 12. Построение
- 13. Немного историиДревнегреческий философ, математикПифагор.570 – 490 гг. до н.э.
- 14. Пентаграмма
- 15. ФибоначчиЛеонардо Пизанский, Фибоначчиок. 1170 – ок. 1250 гг. н.э.Математик средневековой Европы
- 16. ФибоначчиОтношение смежных чисел в этом ряду приближается к золотому сечениюпо мере увеличения ряда
- 17. Золотой прямоугольникПостроим квадрат ABCDНайдем середину стороны AD
- 18. Золотой прямоугольникABFE – золотой прямоугольник
- 19. Золотой прямоугольник
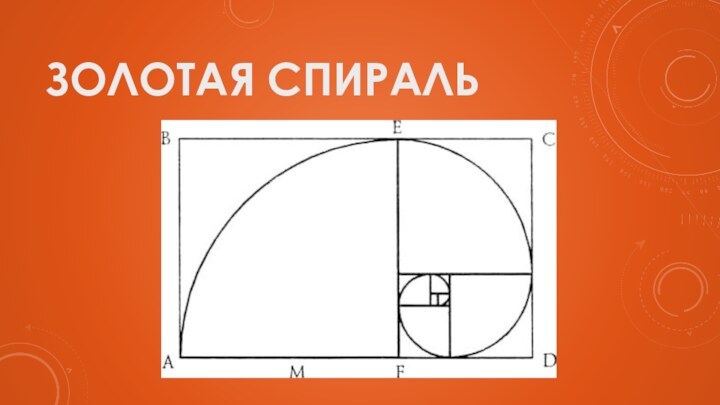
- 20. Золотая спираль
- 22. Подведение итоговТема урокаЗолотое сечениеЗнания и умениядесятичные дроби,
- 23. ЛитератураКовалев Ф.В. Золотое сечение в живописи. К.:
- 24. Скачать презентацию
- 25. Похожие презентации
Одно из самых удивительных явлений и открытий в математике. Что это?




















Слайд 3
Золотое сечение
Что такое отношение?
Отношение – другое название частного,
которое показывает, во сколько раз одно число больше другого,
или какую часть одно число составляет от другого.Что такое пропорция?
Пропорция – равенство двух отношений a : b = c : d.
Слайд 4
Посчитаем?
1. Разделим длину меньшей части отрезка на длину
большей части.
2. Разделим длину большей части отрезка на длину
всего отрезка. Какое число у вас получилось?
Слайд 5
Золотое сечение
Золотое сечение – такое пропорциональное деление целого
отрезка на неравные части, при котором большая часть такого
отрезка относится ко всему отрезку так, как и меньшая часть к большей.Такое отношение приблизительно равно 0,618.
Слайд 11
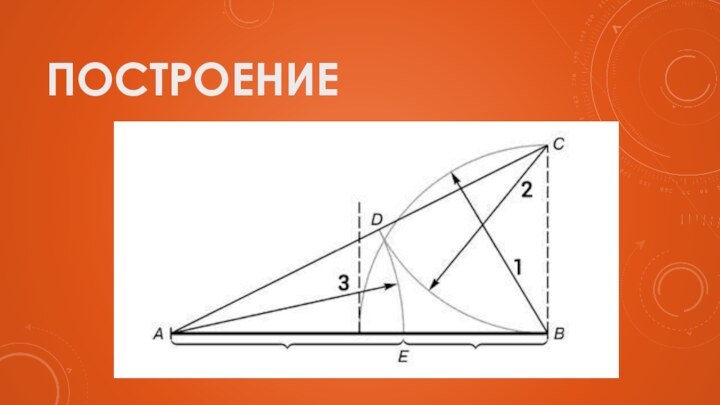
Построение
Начертим отрезок любой длины и назовем его АВ
Построим
отрезок СВ ┴ АВ, равный половине АВ.
Соединим точки А
и С отрезком.На полученном отрезке АС отмечаем точку D так, чтобы новый отрезок CD = BC.
Перенесем длину отрезка AD на отрезок АВ и отметим на нем точку E.
Слайд 15
Фибоначчи
Леонардо Пизанский,
Фибоначчи
ок. 1170 – ок. 1250 гг.
н.э.
Математик средневековой
Европы
Слайд 16
Фибоначчи
Отношение смежных чисел в этом ряду
приближается к
золотому сечению
по мере увеличения ряда
Слайд 17
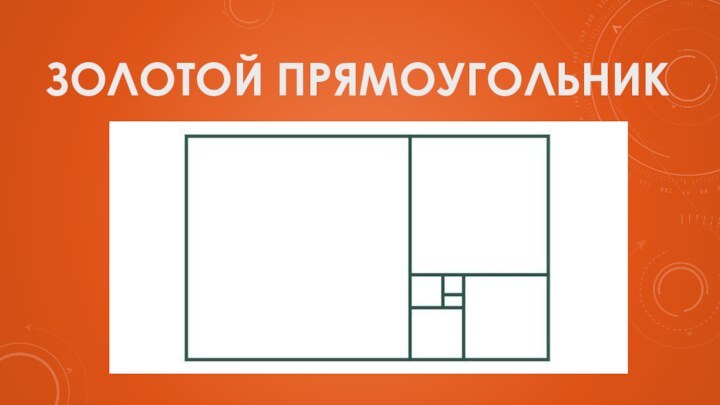
Золотой прямоугольник
Построим квадрат ABCD
Найдем середину стороны AD и
отметим ее точкой M
Измерим длину отрезка МС, чтобы построить
окружность данного радиуса.Проведем окружность с центром в точке М и радиусом МС.
Найдем точку пересечения построенной окружности и продолжения стороны AD. Назовем ее Е.
Достроим фигуру до прямоугольника ABFE.
Слайд 22
Подведение итогов
Тема урока
Золотое сечение
Знания и умения
десятичные дроби, отношение
и пропорция
Построение
деление отрезка, золотой прямоугольник, золотая спираль
«Высшее назначение математики
состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает»- Н. Винер
Слайд 23
Литература
Ковалев Ф.В. Золотое сечение в живописи. К.: Выща
школа, 1989.
Кеплер И. О шестиугольных снежинках. – М., 1982.
Дюрер
А. Дневники, письма, трактаты – Л., М., 1957.Стахов А. Коды золотой пропорции.
https://ru.wikipedia.org/wiki/Золотое_сечение
Видео - http://rutube.ru/video/376a4a360f9f5332d1f550615df80813/
Все изображения, используемые в презентации, принадлежат их владельцам