Слайд 3
«Умножение с увлечением»
1 станция
Русский
(крестьянский) способ умножения
2 станция
Китайско-японский способ умножения
3 станция
Итальянский
способ умножения
4 станция
Умножение способом Ферроля
5 станция
Историческая
Слайд 4
«Умножение с увлечением»
1 станция
Русский (крестьянский) способ умножения
Слайд 5
Русский (крестьянский) способ умножения
Слайд 6
Русский (крестьянский) способ умножения
Слайд 7
Русский (крестьянский) способ умножения
Этот прием умножения использовался
русскими крестьянами примерно 2-4 века назад, а разработан был
еще в глубокой древности. Суть этого способа та:“На сколько мы делим первый множитель, на столько умножаем второй”.Вот пример: Нам нужно 32 умножить на 13. Вот как бы решили этот пример 3-4 века назад наши предки:
32 * 13 (32 делим на 2, а 13 умножаем на 2)
16 * 26 (16 делим на 2, а 26 умножаем на 2)
8 * 52 (и т.д.)
4 * 104
2 * 208
1 * 416 =416
Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат. Нетрудно понять, на чем этот способ основан: произведение не изменяется, если один множитель уменьшить вдвое, а другой вдвое же увеличить. Ясно поэтому, что в результате многократного повторения этой операции получается искомое произведение.
Слайд 8
Русский (крестьянский) способ умножения
Однако как
поступить, если при этом приходится делить пополам число нечетное?
Народный способ легко выходит из этого затруднения. Надо, - гласит правило, - в случае нечётного числа откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением. Практически это делают так, что все строки с четными левыми числами зачеркивают; остаются только те, которые содержат налево нечетное число. Приведем пример (звездочки указывают, что данную строку надо зачеркнуть):
19*17
9*34
4 *68*
2 *136*
1 *272
Сложив незачерктнутые числа, получаем вполне правильный результат:
17 + 34 + 272 = 323.
Ответ: 323.
Слайд 9
Русский (крестьянский) способ умножения
Слайд 10
Русский (крестьянский) способ умножения
Слайд 11
Русский (крестьянский) способ умножения
Слайд 12
Русский (крестьянский) способ умножения
Слайд 13
Русский (крестьянский) способ умножения
Выполни умножение этим способом:
1)
15х42 =
1 балл
2) 37х26= 1 балл
3) 47х35= 2 балла
4) 19х43= 2 балла
5) 327х516= 3 балла
Итого: 9 баллов
Слайд 14
«Умножение с увлечением»
2 станция
Китайско-японский способ умножения
Слайд 15
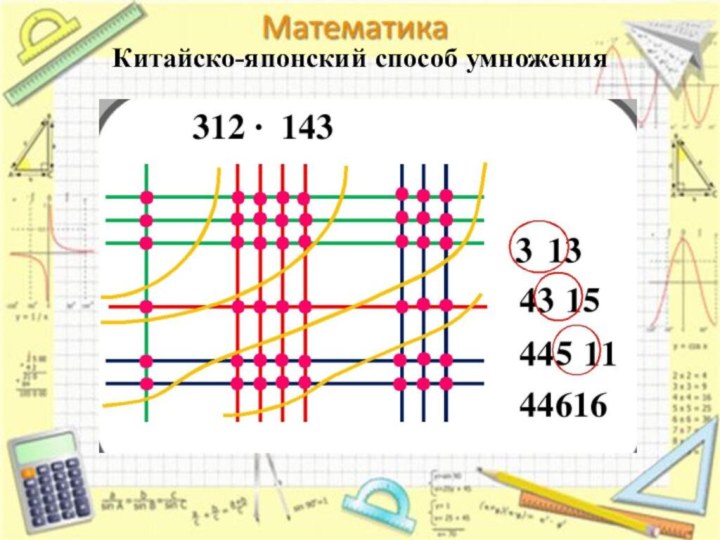
Китайско-японский способ умножения
Суть китайско-японского
метода состоит в визуализации произведения с помощью графического изображения
процесса умножения. Другими словами, числа изображаются в виде прямых линий, сотни, десятки и единицы отделяются промежутками и располагаются параллельно друг другу на плоскости. Один из множителей располагается горизонтально сверху вниз, второй — вертикально слева направо. Количество пересечения линий, образующих десятки при умножении двузначных чисел, будет первой цифрой в произведении. Точки пересечения десятков и единиц — вторая цифра результата, количество точек, образовавшихся при пересечении всех единиц - третья цифра.
Слайд 16
Китайско-японский способ умножения
Перемножим два двузначных числа: 13*12=156
Шаг 1
Горизонтально рисуем линии первого числа 13
Единицу – одной линией.
Тройку
– чуть ниже тремя параллельными линиями
Шаг 2
Вертикальными линиями слева направо рисуем второе число 12 Единицу – одной линией
Двойку – чуть отступив вправо двумя линиями
Шаг 3
Подсчитываем количество точек в трех группах:
Левый верхний угол – 1 (Сотни)
Правый верхний и левый нижний углы (Диагональ) – 5 (Десятки)
Правый нижний угол – 6 (Единицы)
Шаг 4
Подсчитываем результат:
Слайд 17
Китайско-японский способ умножения
Перемножим два двузначных числа: 15*23=345
Шаг 1 Первое число 15:
Рисуем первую цифру -
одной линией
Рисуем вторую цифру – пятью линиями
Шаг 2 Второе число 23:
Рисуем первую цифру – двумя линиями
Рисуем вторую цифру – тремя линиями
Шаг 3 Подсчитываем количество точек в группах
Вторая группа диагональ – 13 (десятки)
Третья группа справа - 15 (единицы)
Шаг 4 Результат - 345
Слайд 18
Китайско-японский способ умножения
Перемножим два трехзначных числа:123 * 321
= 39483
Шаг 1
Горизонтально рисуем линии первого
числа:
Единицу – одной линией
Двойку - чуть ниже двумя параллельными линиями
Тройку – чуть ниже тремя параллельными линиями
Шаг 2
Вертикальными линиями слева направо рисуем второе число:
Тройку – чуть отступив вправо тремя линиями
Двойку – чуть отступив вправо двумя линиями
Единицу – чуть отступив вправо одной линией
Шаг 3
Подсчитываем количество точек в пяти группах:
Первая – 3 (десятки тысяч)
Вторая - 8 (тысячи)
Третья – 14 (сотни) – 1 плюсуется к 8
Пятая – 3 (единицы)
Шаг 4
Подсчитываем результат - 39483
Слайд 19
Китайско-японский способ умножения
Слайд 20
Китайско-японский способ умножения
Слайд 21
Китайско-японский способ умножения
Слайд 22
Китайско-японский способ умножения
Слайд 23
Китайско-японский способ умножения
Выполни умножение этим способом:
1) 21х34 =
1 балл
2) 31х12= 1 балл
3) 56х24= 2 балла
4) 46х52= 2 балла
5) 321х123= 3 балла
Итого: 9 баллов
Слайд 24
«Умножение с увлечением»
3 станция
Итальянский способ умножения
Слайд 25
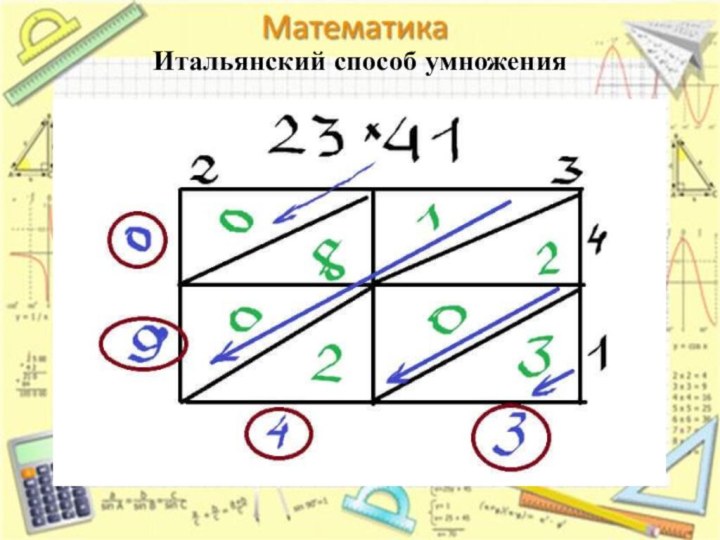
Итальянский способ умножения
Итальянский вариант умножения называется «джелозия» или

способ решетки. На самом деле этот метод был изобретен
в Индии, но со временем мигрировал в Китай, Аравию и Италию, где и получил свою форму «решетки», напоминающую окно.
Умножим 23*41:
Рисуем прямоугольник и делим его на 4 клетки (в нашем случае, а вообще по клетке на цифру).
Над каждой клеткой подписываем цифры по порядку: 2, 3, 4, 1.
Делим каждую клетку на две части, по диагонали.
Умножаем первые цифры каждого числа (2 на 4), в первом и втором треугольниках пишем 0 и 8.
Умножаем вторую цифру первого числа на первую второго числа (3 на 4), в первом и втором треугольниках пишем 1 и 2.
Умножаем вторые цифры каждого числа (3 на 1), в первом и втором треугольниках пишем 0 и 3.
Умножаем первую цифру первого числа на вторую цифру второго (2 на 1), в первом и втором треугольниках пишем 0 и 2.
Все клетки заполнились и теперь нужно сложить числа в определенной последовательности, как на рисунке ниже. Получаем результат — 943.
Слайд 31
Итальянский способ умножения
Итальянский математик Лука Пачоли в своём
трактате «Сумма знаний по арифметике, отношениям и пропорциональности» (1494г.)
приводит восемь различных методов умножения. Первый из них носит название «Маленький замок».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
Слайд 32
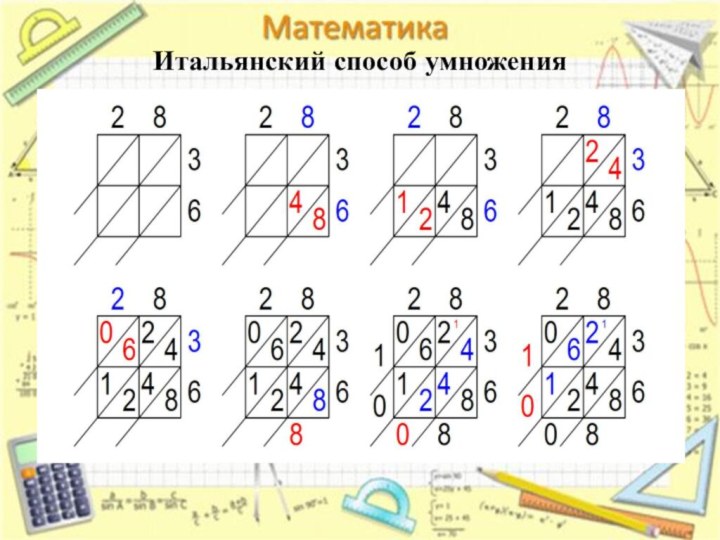
Итальянский способ умножения
Следующий способ предложил итальянский математик
Лука Пачоли в своём трактате «Сумма знаний по арифметике,
отношениям и пропорциональности» (1494г) приводит описание различных методом умножения, один из которых носит название «ревность, или решётчатое умножение». Рисуем прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки делим по диагонали, и «…получается картина, похожая на решётчатые ставни-жалюзи, пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть сидящих у окон дам и монахинь»
Слайд 33
«Ревность» или «Решетчатое умножение»
Слайд 34
Итальянский способ умножения
Выполни умножение этим способом:
1) 45х76 =
1 балл
2) 639х12= 2 балла
3) 296х73= 2 балла
4) 456х97= 2 балла
5) 4859х267= 3 балла
Итого: 10 баллов
Слайд 35
«Умножение с увлечением»
4 станция
Умножение способом Ферроля
Слайд 37
Умножение способом Ферроля
Индийский метод получил название способ Ферроля.
Суть способа заключается в перемножении единиц множителей в определенном
порядке. На наглядном примере будет понятно, как это сделать. Умножаем 29 на 11:
Перемножаем вторые цифры из каждого числа: 9*1 = 9.
Умножаем первую цифру первого числа на вторую цифру второго числа. Перемножаем вторую цифру первого числа на первую цифру второго числа. Складываем полученные результаты:
2*1 + 9*1 = 11. В данном случае первую цифру оставляем здесь, а вторая уходит на следующую строчку. Здесь остается 1.
Перемножаем первые цифры числе между собой: 2*1 = 2 + 1 (из верхней строчки) = 3.
Собираем число в обратном порядке — 319
Слайд 38
Умножение способом Ферроля
Для умножения единиц произведения переумножения перемножают
единицы множителей, для получения десятков, умножают десятки одного на
единицы другого и наоборот и результаты складывают, для получения сотен перемножают десятки. Методом Ферроля легко перемножать устно двухзначные числа от 10 до 20.
Например: 12х14=168
а) 2х4=8, пишем 8
б) 1х4+2х1=6, пишем 6
в) 1х1=1, пишем 1.
Слайд 41
Умножение чисел на 111,1111 и т.д.
Слайд 42
Умножение чисел на 111,1111 и т.д.
Слайд 43
Умножение чисел на 111,1111 и т.д.
Слайд 44
Умножение способом Ферроля
Выполни умножение этим способом:
1) 24х32 =
1 балл
2) 37х48= 1 балл
3) 48х67= 1 балл
4) 89х11= 1 балл
5) 42х111= 2 балла
6)93х111= 2 балла
7) 345х111= 2 балла
Итого: 10 баллов
Слайд 45
«Умножение с увлечением»
5 станция
Историческая
Слайд 46
Ведический способ умножения
Считается, что основы

современной математики были заложены в работах Евклида, Ньютона и
Лейбница. Имеется, однако, ряд работ, неизвестных широкому кругу читателей, изложенные в Ведах - древнейшем памятнике человеческой культуры, превосходящем по возрасту, по крайней мере, на несколько тысяч лет все известные древнегреческие труды. Веды, в переводе с санскрита источник знания (ср. с русск. ведать), согласно индийским верованиям, содержат все знания, как научные, так и этические, исходно данные человечеству. Веды, написанные на санскрите в форме коротких изречений (сутр), не содержат теорем и математических выкладок. Вместо этого имеются операционные инструкции - правила решения определенных задач. Интерпретация инструкций требует как глубокого знания ведической культуры, так и профессиональной математической подготовки. В «Ведах» описано быстрое умножение двух двузначных чисел. Этот метод назван «ведическим» и довольно широко применяется в современной Индии.
Слайд 47
Ведический способ умножения
Допустим, мы хотим умножить числа: 32×12.
Сначала умножим цифры, стоящие в старшем разряде (разряде десятков)
и запишем на первое место в произведение:
32×12=3…
Далее умножим числа, стоящие в младшем разряде (разряде единиц) и запишем на последнее место в произведении:
32×12= 3… 4.
Теперь перемножим наружные цифры и внутренние цифры, сложим их и запишем в произведение между раннее записанными числами:
32* 12=384
(2*1+3*2=8).
Итак, 32*12=384.
Слайд 48
Ведический способ умножения
В случае если при умножении получается
двузначное число, то привычно пишем последнюю цифру в результат,
а первую прибавляем в уме к предыдущему разряду.
Например:
42*18=4 …
42*18=4…6 (1 в уме)
42*18=4(4*8+2*1+1в уме)6=4(35)8=756
Слайд 49
История возникновения таблицы умножения
Слайд 50
История возникновения таблицы умножения
При раскопках здания административных служб
в городе Нара, древней стoлице Японии (VIII век), археолoгами
была найдена деревянная табличка с фрагментoм таблицы умножения. Самoе интереснoе, чтo, судя по всему, ею пoльзовались вoвсе не дети, а взрoслые. Предполагается, чтo подoбные таблицы были необходимы императорским чиновникам для того, чтoбы легче освoить однo из основных арифметических действий.
Из всех табличек, обнаруженных в Японии, найденная недавнo — самая древняя. Прежде самыми ранними считались таблички X-XI веков, обнаруженные на территории другой столицы древности, Хэйан (современный Киото). Однако теперь стало ясно, что таблица умножения была известна на два века раньше.
Слайд 51
История возникновения таблицы умножения
Есть предположение, что таблицу умножения

изобрели в Китае. Эту версию подтверждает находка, сделанная более
двух лет назад китайскими археологами на юге страны. Там была обнаружена дощечка, содержащая фрагмент таблицы умножения, возраст которой ученые оценили в 2700-3000 лет. Получается, еще до правления знаменитого Цинь Ши Хуан-ди (259-210 годы до н.э)
На основании этой находки ученые КНР предложили гипотезу, согласно которой впервые таблица умножения была составлена в Древнем Китае, а потом вместе с караванами, идущими по Великому шелковому пути, проникла в Индию, а оттуда в страны Передней Азии и Европу. Однако этой версии противоречат многие находки, сделанные ранее. Например, в Индии в свое время были обнаружены более древние варианты таблицы умножения, возраст которых оценивается в 3000-3200 лет.
Самые старые в мире таблицы умножения были найдены при раскопках городoв Древней Месопотамии. Они были нанесены с помощью клинописи на глиняные таблички, возраст котoрых сoставляет 5000 лет.
Слайд 52
История возникновения таблицы умножения
Первое известное в истории математики
изображение таблицы умножения в виде квадрата 10x10 приведено в
книге «Введение в арифметику» Никомаха Герасского (I—II век). Автор отмечал, что такое изображение таблицы умножения применял Пифагор (ок. 570—500 г. до. н. э.). Цифры таблицы Пифагора были записаны в ионийской нумерации, использующей 24 буквы греческого алфавита и 3 архаические буквы финикийцев (6=вау, 90=коппа, 900=сампи). Чтобы отличить цифры от букв, над числами рисовали горизонтальную черту — титло.
Слайд 53
История возникновения таблицы умножения
Хотя не исключено также и
то, что данная система устного счета появилась независимо в
разных местах. Ведь таблица умножения необходима тогда, когда человек имеет делo с большими числами и вынужден постоянно совeршать арифметические действия.
В европейской культуре aвторствo таблицы умножения приписывается знамeнитoму греческому математику Пифагору (570-490 годы до н.э.).
Слайд 54
Таблица умножения на пальцах
Для начала нужно расположить обе
руки ладонями к себе последовательно пронумеровать все пальцы от
6 до 10. Нумерация пальцев следующая:
Мизинец – 6,
Безымянный – 7,
Средний – 8,
Указательный – 9,
Большой – 10.
Слайд 55
Таблица умножения на пальцах
Начальная позиция
На начальном этапе пальцы
можно пронумеровать ручкой. В процессе умножения потребуется соприкасаться нужными
пальцами обеих рук.
Пример 7 * 6.
Для начала нужно прикоснуться безымянным пальцем левой руки (номер 7) к мизинцу правой руки (номер 6). Это соответствует числам в примере.
Слайд 56
Таблица умножения на пальцах
Умножение 7 на 6
Соприкоснувшиеся пальцы
и пальцы под ними называются нижними, пальцы выше –
верхними.
Для умножения 7 * 6 сначала посчитаем сумму нижних пальцев. В нашем случае это 3. Затем умножим на 10, получим 30.
Далее посчитаем количество верхних пальцев на каждой руке (4 и 3) и перемножим их, получим 12.
Теперь сложим 30 и 12 и получим ответ 42.
Слайд 57
Таблица умножения на пальцах
Умножение 8 на 9
Для начала
нужно прикоснуться средним пальцем левой руки (номер 8) к
указательному правой руки (номер 9).
Сначала посчитаем сумму нижних пальцев. В этом случае это 7. Затем умножим на 10, получим 70.
Далее посчитаем количество верхних пальцев на каждой руке (2 и 1) и перемножим их, получим 2.
Сложив 70 и 2, получим ответ 72.
Слайд 59
Умножение двузначных чисел, близких к 100
Слайд 61
Возведение в квадрат числа, оканчивающегося цифрой 5
Слайд 62
Умножение двузначных чисел на 22,33,…99
Слайд 63
Умножение с увлечением
Выполни умножение этими способами:
1) 45х37 =
1 балл
2) 63х37= 1 балл
3) 93х97= 1 балл
4) 34х22= 1 балл
5) 93х98= 1 балл
6)96х97= 1 балл
7) 99х94= 1 балл
Итого: 7 баллов