Слайд 2
Математическая статистика - это раздел математики, который имеет
своим предметом изучение методов сбора, систематизации, обработки и использования
статистических данных для получения научно обоснованных выводов и принятия решений.
При этом под статистическими данными понимается совокупность чисел, которые представляют количественные характеристики интересующих нас признаков изучаемых объектов. Статистические данные получаются в результате специально поставленных опытов, наблюдений.
Слайд 3
Данные могут быть представлены
- графически;
в виде ряда данных
;
в виде таблиц.
Слайд 4
Графическое представление информации.
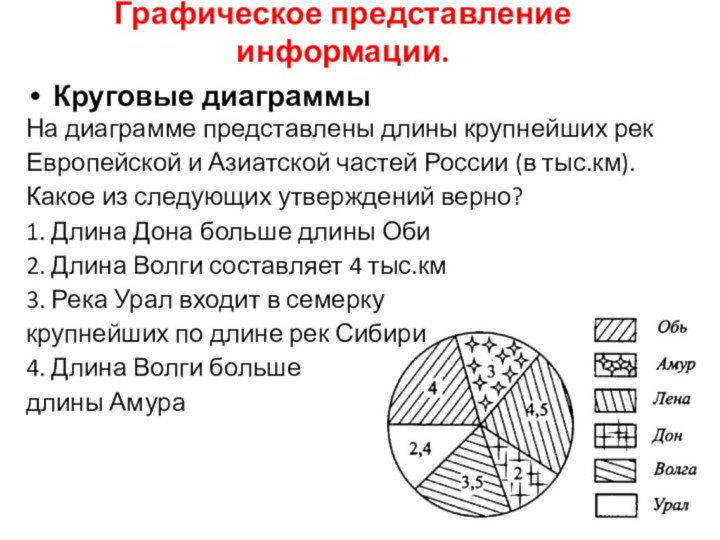
Круговые диаграммы
На диаграмме представлены длины крупнейших
рек Европейской и Азиатской частей России (в тыс.км). Какое
из следующих утверждений верно?
1. Длина Дона больше длины Оби
2. Длина Волги составляет 4 тыс.км
3. Река Урал входит в семерку
крупнейших по длине рек Сибири
4. Длина Волги больше
длины Амура
Слайд 5
Графическое представление информации.
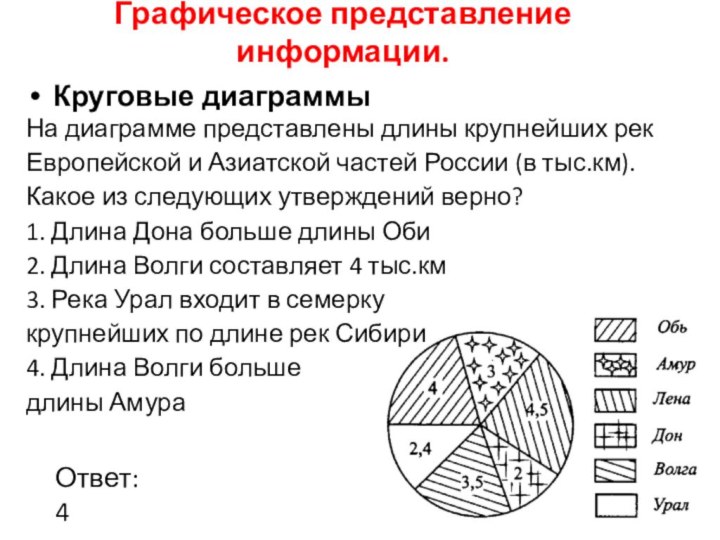
Круговые диаграммы
На диаграмме представлены длины крупнейших
рек Европейской и Азиатской частей России (в тыс.км). Какое
из следующих утверждений верно?
1. Длина Дона больше длины Оби
2. Длина Волги составляет 4 тыс.км
3. Река Урал входит в семерку
крупнейших по длине рек Сибири
4. Длина Волги больше
длины Амура
Ответ: 4
Слайд 6
Графическое представление информации.
Круговые диаграммы
На диаграмме показано содержание питательных
веществ в рисе.
Определите по диаграмме, в каких пределах находится
содержание углеводородов.
1) 0 – 20 % 2) 20 – 50 % 3) 50 – 70 % 4) 70 – 100 %
Ответ: 4
Слайд 7
Графическое представление информации.
Круговые диаграммы
На диаграмме показано содержание питательных
веществ в рисе.
Определите по диаграмме, содержание каких веществ преобладает.
1)
белки 2) жиры 3) углеводы 4) прочее
Ответ: 3
Слайд 8
Графическое представление информации.
Круговые диаграммы
На диаграмме показано содержание питательных
веществ в рисе.
Определите по диаграмме, сколько примерно белков содержится
в 500 г риса.
1)около 7 г 2)около 35 г 3)около 70 г 4)около 350 г
Ответ: 2
Слайд 9
Графическое представление информации.
Круговые диаграммы
На диаграмме показано содержание питательных
веществ в рисе.
Определите по диаграмме, какая примерно масса риса
содержит 300 г углеводов.
1) около 220 г 2) около 400 г 3) около 1,5 кг 4)около 3 кг
Слайд 10
Графическое представление информации.
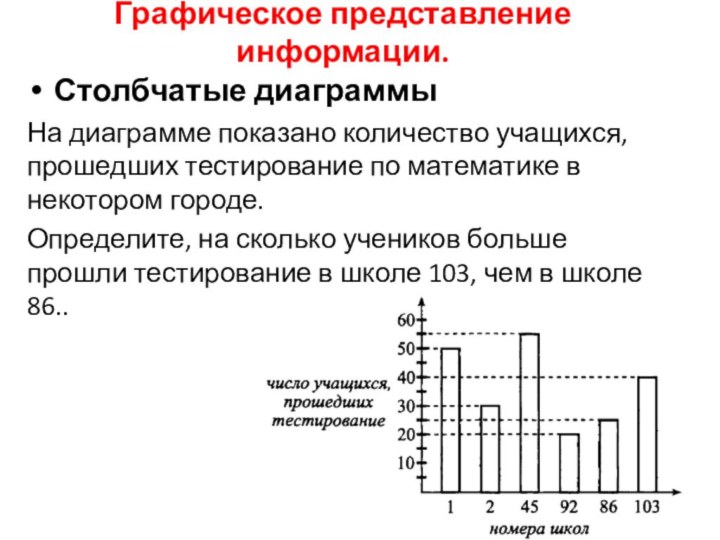
Столбчатые диаграммы
На диаграмме показано количество учащихся,
прошедших тестирование по математике в некотором городе.
Определите номер
школы, занявшей второе место по числу прошедших тестирование.
Слайд 11
Графическое представление информации.
Столбчатые диаграммы
На диаграмме показано количество учащихся,
прошедших тестирование по математике в некотором городе.
Определите, на
сколько учеников больше прошли тестирование в школе 103, чем в школе 86..
Слайд 12
Ряд данных и таблица распределения данных
Например. Результаты написания
контрольной работы по математике для класса из 20 человек
можно представить в виде следующего ряда данных:3,4,4,5,3,4,3,3,3,5,5,4,5,4,5,3,3,3,4,3. Эту же информацию можно представить в виде таблицы:
Такую таблицу называют таблицей частот.
Слайд 13
Числовые характеристики данных
Среднее арифметическое ряда чисел -
частное от деления суммы этих чисел на число
слагаемых
Размах ряда чисел - разность между наибольшим и наименьшим из этих чисел
Мода ряда чисел – число наиболее часто встречающееся в данном ряду
Медианой упорядоченного ряда чисел с нечётным числом членов называется среднее в ряду число;
с чётным числом членов среднее арифметическое чисел, записанных посередине
Слайд 14
1. Размах ряда 5-3 =
2
2. Мода ряда число 3
(т.к. встречается чаще всех)
Среднее арифметическое (3∙9+4∙6+5∙5):20=3,8
Медиана ряда равна 4.
Вернемся к нашей задаче.
Слайд 16
Теория вероятностей изучает объективные закономерности массовых случайных событий.
Она является теоретической базой для математической статистики, занимающейся разработкой
методов сбора, описания и обработки результатов наблюдений.
Теория вероятностей есть раздел математики, в котором изучаются случайные явления (события) и выявляются закономерности при массовом их повторении.
Слайд 17
1. Случайное событие (СС)- это событие, которое либо
произойдёт, либо нет.
2. Каждое случайное событие (СС) иметь свою
вероятность произойти (сбыться, реализоваться).
3. Испытание – любое действие, которое может привести к одному или нескольким результатам.
4. Исход - конечный результат испытания. Значит испытание может иметь один или несколько исходов.
5. Благоприятный исход – желаемый исход.
Слайд 18
Запомни:
m – число (количество) благоприятных исходов,
n – число
(количество) всех исходов.
m – число (количество) благоприятных исходов,
n –
число (количество) всех исходов.
m – число (количество) благоприятных исходов,
n – число (количество) всех исходов.
Слайд 23
Два события А и В называют несовместными, если
отсутствуют исходы, благоприятствующие одновременно как событию А, так и
событию В.
Пример:
при бросании кубика события «выпало число 3» и «выпало четное число» несовместны, а события «выпало число больше 3» и «выпало четное число» совместны.
Слайд 24
Пусть событие С означает, что произошло хотя бы
одно из событий А и В. Тогда С называют
объединением событий А и В, пишут С=А В.
Если события А и В несовместны, то вероятность их объединения равна сумме вероятностей событий А и В:
Р(А В)= Р(А) + Р(В)
Слайд 27
Два события А и В называют независимыми, если
вероятность каждого из них не зависит от появления или
непоявления другого события.
Пример:
Выполним последовательно два подбрасывания монеты. Тогда события «при первом подбрасывании выпала решка» и «при втором подбрасывании выпал орел» являются независимыми: вероятность каждого из них рана 0,5 независимо от того, что произошло при другом подбрасывании.
Слайд 32
ООО
ООР
ОРО
ОРР
РОО
РОР
РРО
РРР
МОНЕТА
I подбрасывание
I I подбрасывание
III подбр.
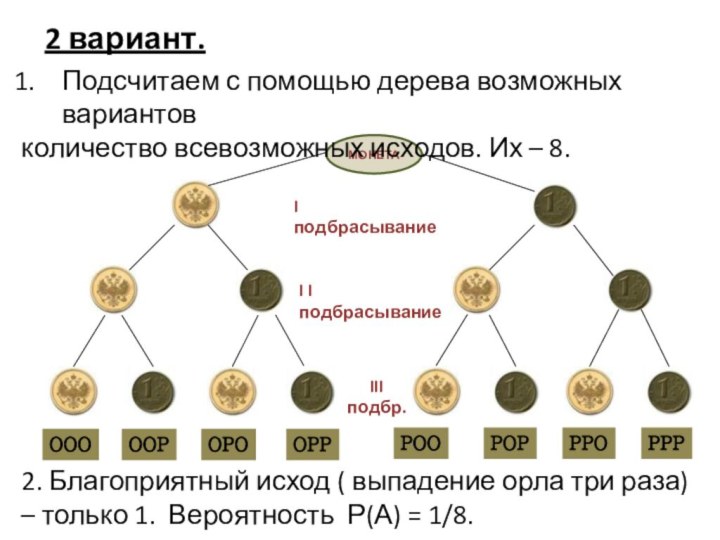
2 вариант.
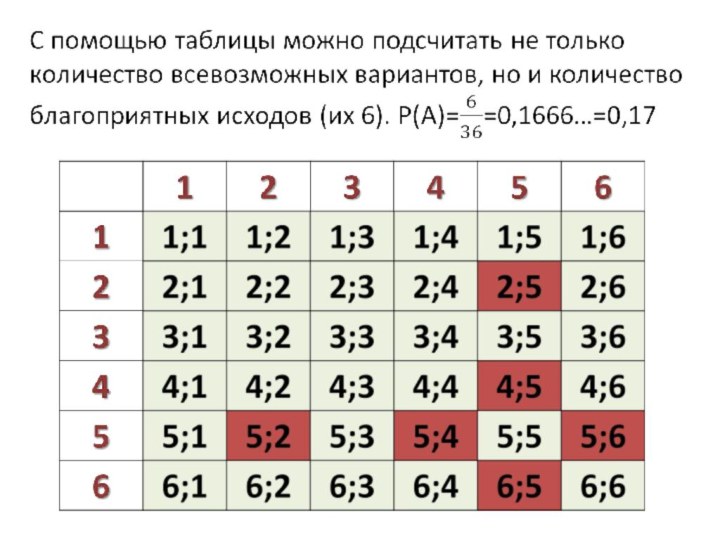
Подсчитаем с
помощью дерева возможных вариантов
количество всевозможных исходов. Их – 8.
2.
Благоприятный исход ( выпадение орла три раза) – только 1. Вероятность Р(А) = 1/8.
Слайд 33
Варианты всевозможных исходов можно подсчитать тремя способами.
Слайд 40
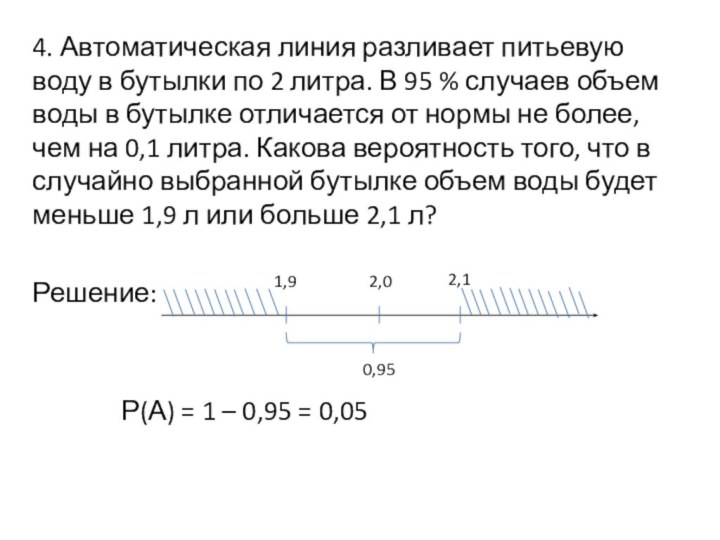
4. Автоматическая линия разливает питьевую воду в бутылки
по 2 литра. В 95 % случаев объем воды
в бутылке отличается от нормы не более, чем на 0,1 литра. Какова вероятность того, что в случайно выбранной бутылке объем воды будет меньше 1,9 л или больше 2,1 л?
Решение:
Р(А) = 1 – 0,95 = 0,05
1,9
2,1
2,0
0,95
Слайд 44
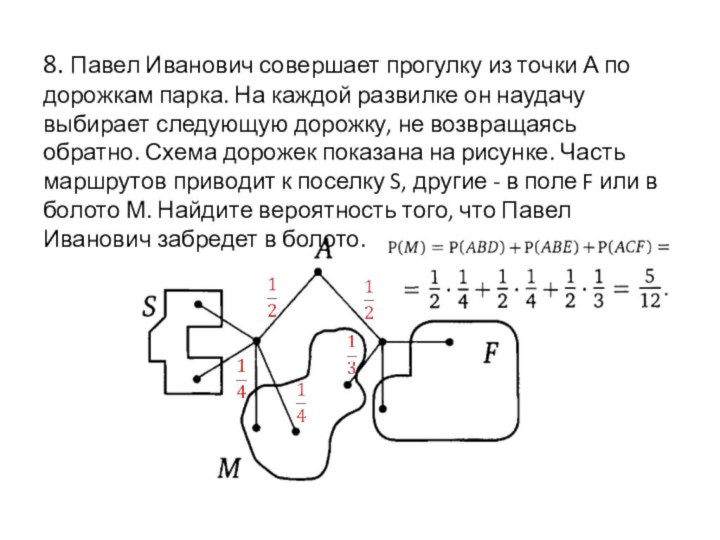
8. Павел Иванович совершает прогулку из точки А
по дорожкам парка. На каждой развилке он наудачу выбирает
следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Часть маршрутов приводит к поселку S, другие - в поле F или в болото М. Найдите вероятность того, что Павел Иванович забредет в болото.
Слайд 45
Спасибо за внимание
Удачи на экзамене.