Презентация на тему к уроку геометрии Построение правильных многоугольников

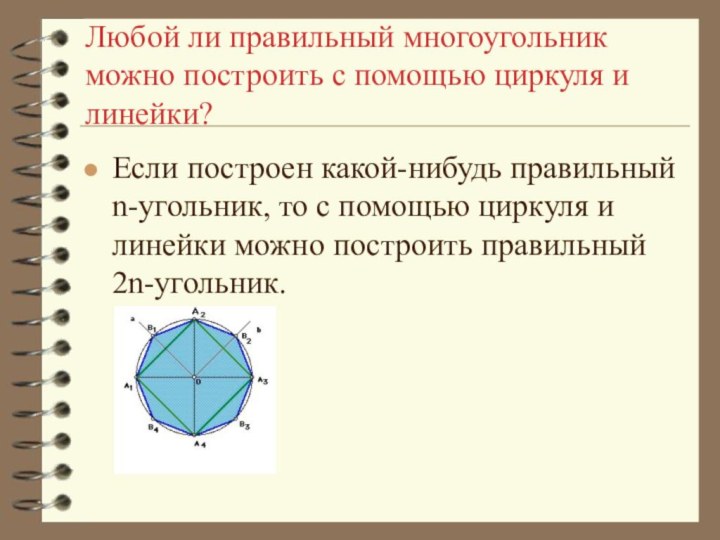
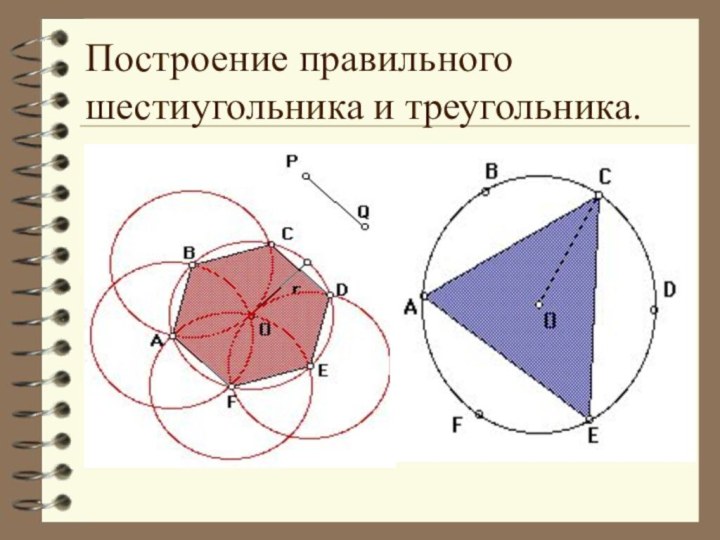
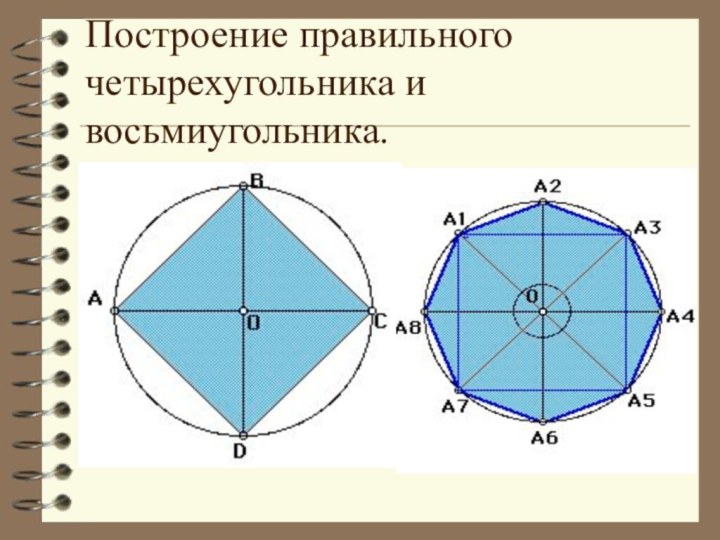
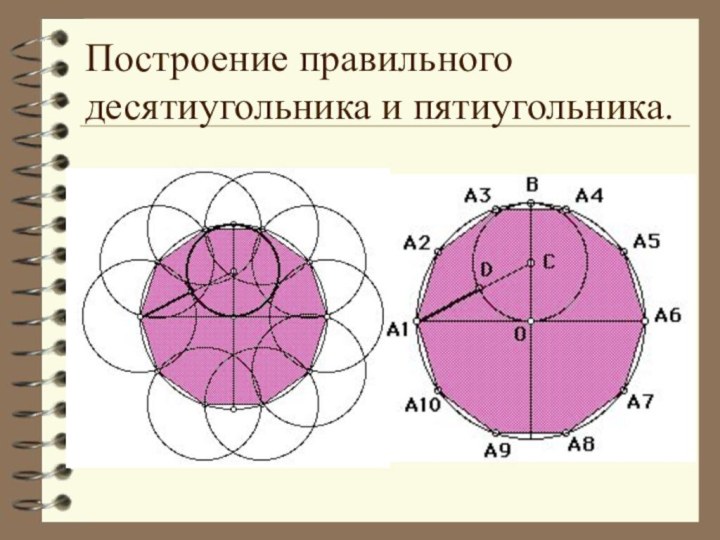
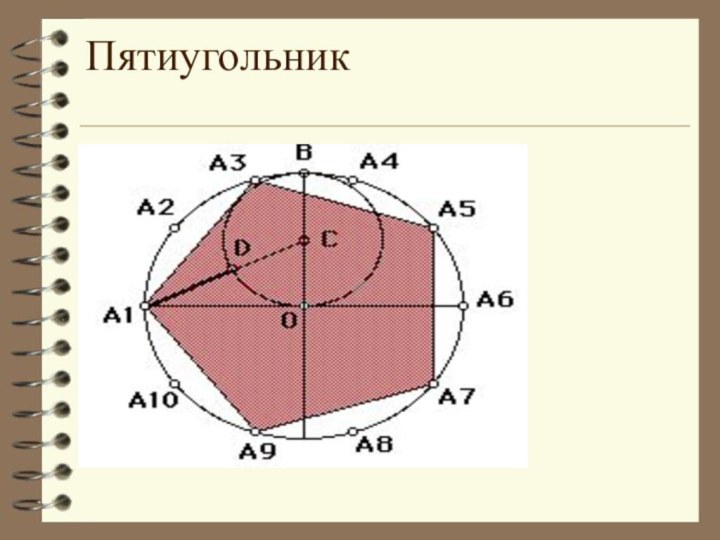
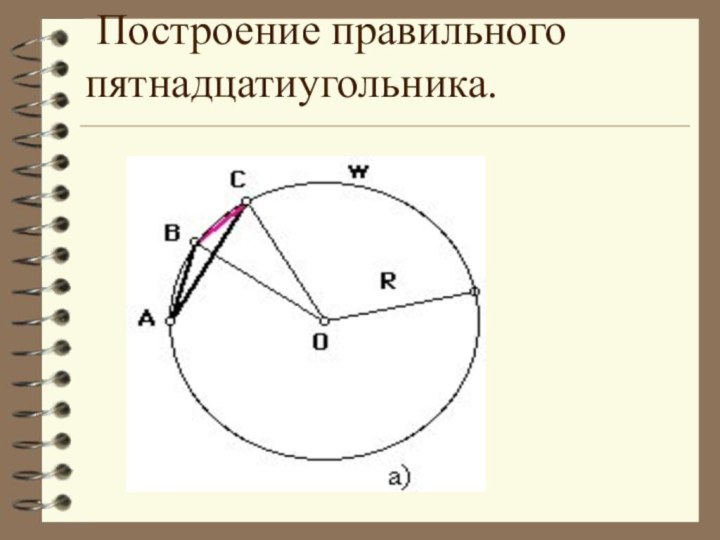
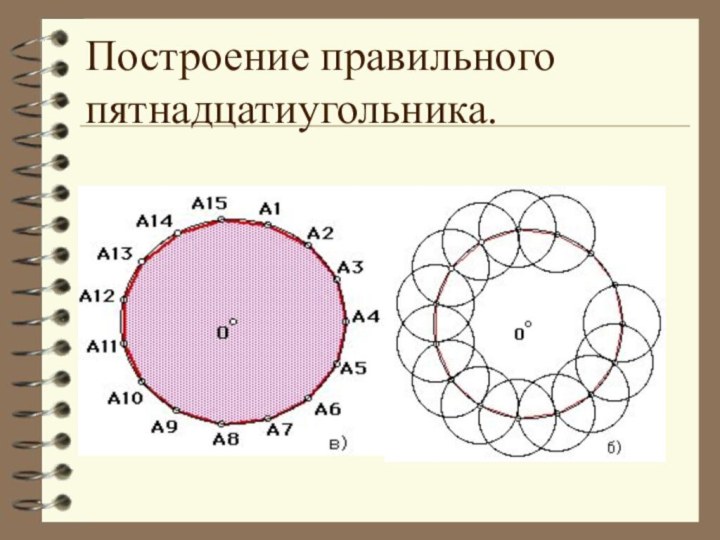
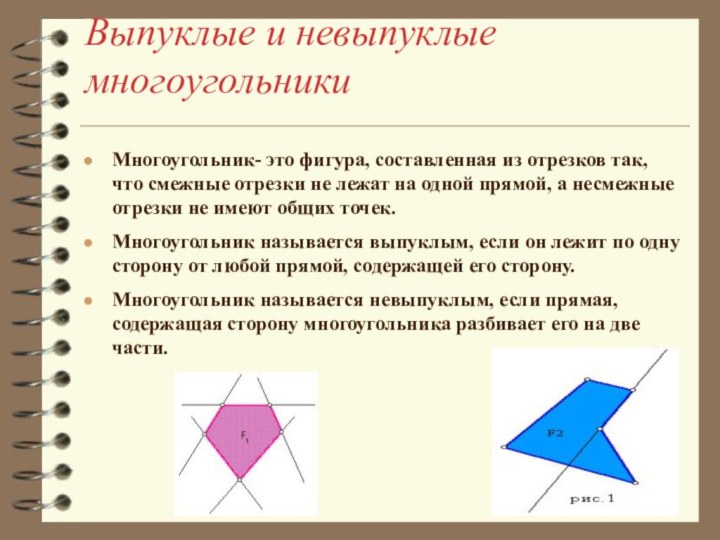
отрезков так, что смежные отрезки не лежат на одной

прямой, а несмежные отрезки не имеют общих точек.
Многоугольник называется выпуклым, если он лежит по одну сторону от любой прямой, содержащей его сторону.
Многоугольник называется невыпуклым, если прямая, содержащая сторону многоугольника разбивает его на две части.

- это наличие разных типов симметрий, или самосовмещений. Рассмотрим

с этой точки зрения виды четырехугольников

выпуклого n-угольника равна

180*(n-2)

Cумма внешних углов многоугольника, равна 360 градусов, и не зависит не только от формы многоугольника, но и от числа его сторон!

углы равны и все стороны равны.

и притом только одну, и также в любой правильный

многоугольник можно вписать окружность, и притом только одну. Центры описанной около правильного многоугольника и вписанной в него окружностей совпадают. Правильные многоугольники всегда выпуклые, но существуют и самопересекающиеся замкнутые ломаные, имеющие равные звенья и углы. Фигуры такого вида называются правильными звездчатыми многоугольниками или полиграммами, по аналогии с пентаграммой - правильной пятиконечной звездой

циркуля и линейки?
Если построен какой-нибудь правильный n-угольник, то с

помощью циркуля и линейки можно построить правильный 2n-угольник.

возможно тогда и только тогда, когда число n имеет

следующее разложение на множители: