они энергично поддержали друг друга и быстро зашагали к
совершенству.»Ж.А. Лагранж
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть









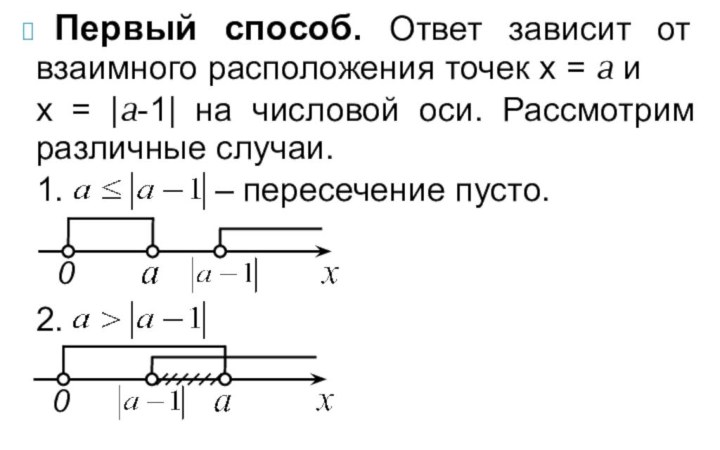









1. – пересечение пусто.
0
2.
0
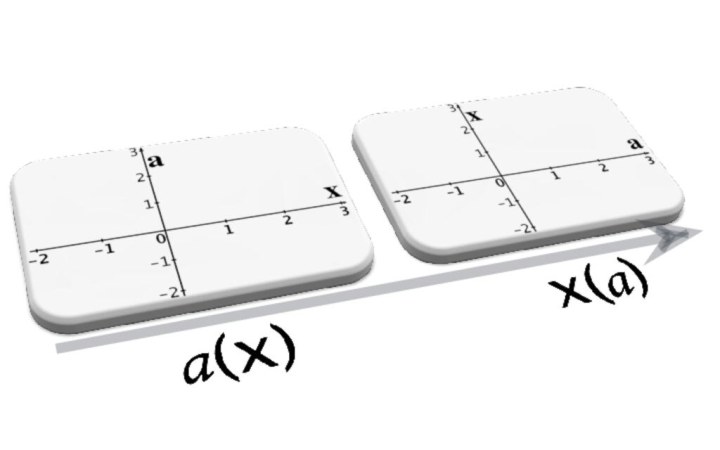
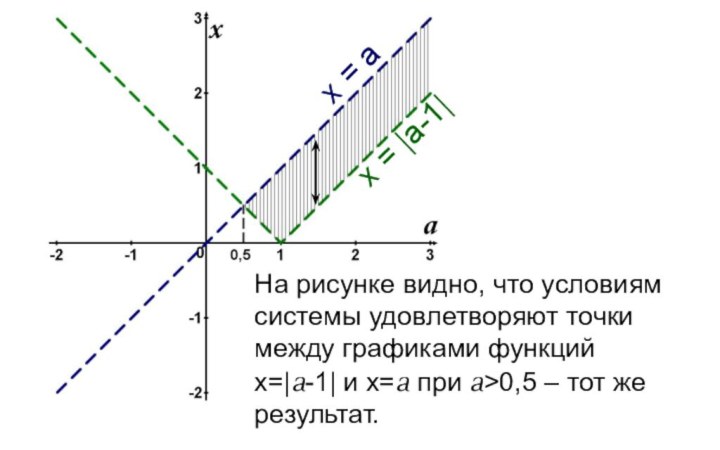
x = a
x = |a-1|
и среди решений есть x=2.
Ответ: 1; a=2,5.
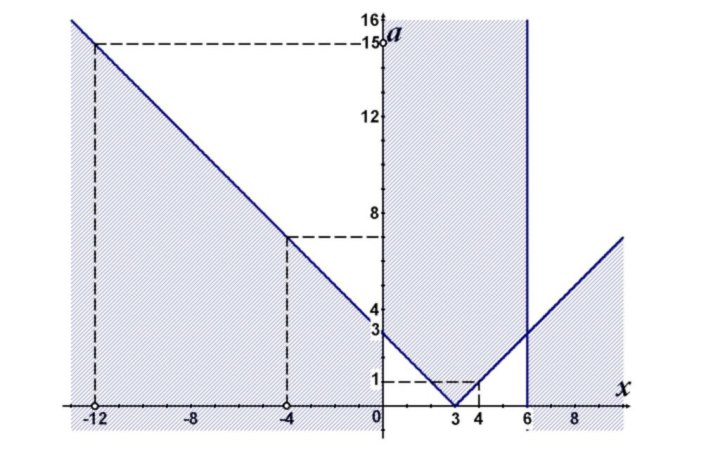
где p>15,
То есть конечным множеством значений
a является промежуток [1;15). Сумма целых значений равна 105.
Ответ: 105.