тела
Полуправильные многогранники
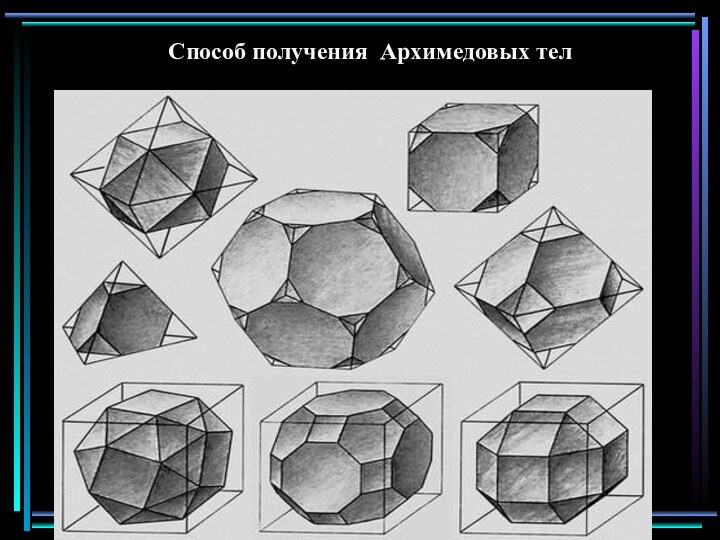
Известно еще множество совершенных тел, получивших название полуправильных
многогранников илиАрхимедовых тел. У них также все многогранные углы равны и все грани – правильные многоугольники, но несколько разных типов. Существует 13 полуправильных многогранников, открытие которых приписывается Архимеду.Архимедовы тела: (а) усеченный тетраэдр, (б) усеченный куб, (в) усеченный октаэдр, (г) усеченный додекаэдр, (д) усеченный икосаэдр
(а)
(б)
(в)
(д)
(г)
Рис.1