- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Чи такі вони прості ці прості числа?
Содержание
- 2. Моє кредо«Людина лише там чогось домагається, де вона сама вірить у свої сили»
- 3. Чи такі вони прості ці прості числа?«Числа
- 4. Актуальність дослідження. Властивості подільності числа повністю визначаються
- 5. Мета. Дослідження закономірностей простих чисел і виявлення
- 6. Завдання.- Показати важливість і необхідність вивчення простих
- 7. Об'єкт дослідження.Прості числа. Предмет дослідження.Використання простих чисел при вирішенні математичних завдань.
- 8. Практична значимість.Результати дослідження будуть використані для вивчення
- 9. ВступЧОТИРИ розділи дослідженьВисновкиЛітератураСтруктурароботи
- 10. Простим числом ми називаємо кожне натуральне число,
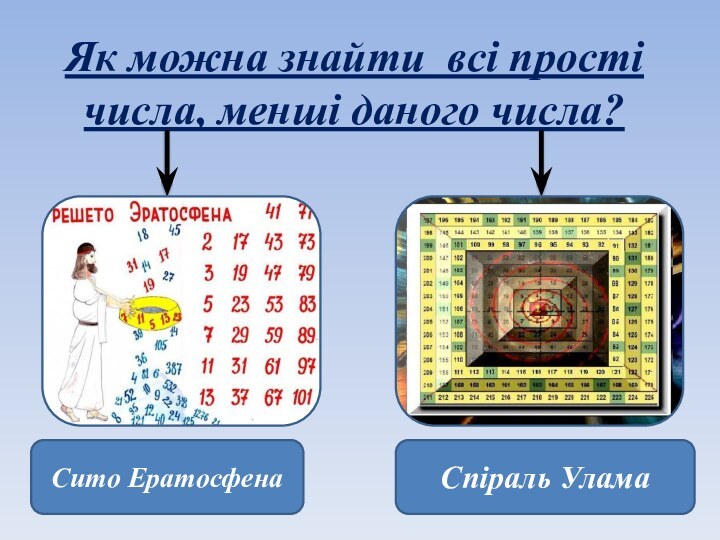
- 12. Як можна знайти всі прості числа, менші даного числа?Сито ЕратосфенаСпіраль Улама
- 13. 2, 3, 5, 7, 11, 13, 17,
- 14. Декілька нерозв’язаних задач2. Ми не знаємо, чи
- 15. 15717Прості числа і містика
- 16. Район дослідження: Швайківська ЗОШОб'єкти спостережень і досліджень:
- 18. Скачать презентацию
- 19. Похожие презентации
















Слайд 3
Чи такі вони прості ці прості числа?
«Числа керують
світом”, - казали піфагорійці. Це, звичайно, містика. Але числа
дають змогу людині керувати світом, і в цьому нас переконує увесь хід розвитку науки й техніки наших днів.Л.О. Дородницин
Слайд 4 Актуальність дослідження. Властивості подільності числа повністю визначаються його
розкладанням на прості множники. Основна теорема арифметики стверджує, що
кожне натуральне число, більше одиниці, представимо у вигляді добутку простих чисел, причому єдиним способом з точністю до порядку слідування співмножників. Таким чином, прості числа — елементарні «будівельні блоки» натуральних чисел.Слайд 5 Мета. Дослідження закономірностей простих чисел і виявлення їх
ролі в курсі математики.
Завдання.
- Розглянути поняття простих чисел
і методи їх обчислення.- Виявити цікаві властивості простих чисел.
Слайд 6
Завдання.
- Показати важливість і необхідність вивчення простих чисел,
і нерозв'язності в даний час деяких гіпотез пов'язаних з
ними.- Провести власний досвід дослідження щодо застосування простих чисел при вирішенні завдань.
Слайд 7
Об'єкт дослідження.
Прості числа.
Предмет дослідження.
Використання простих чисел при
вирішенні математичних завдань.
Слайд 8
Практична значимість.
Результати дослідження будуть використані для вивчення даної
теми на заняттях математичного гуртка, при підготовці учнів до
математичних олімпіад та здачі ЗНО.«Жодна інша галузь теорії чисел не насичена настільки таємничістю і елегантністю, як вивчення простих чисел, цих непокірних, дражливих чисел, що не хочуть ділитися без остачі ні на яке ціле число, крім себе й одиниці», – Мартин Гарднер.
Слайд 10 Простим числом ми називаємо кожне натуральне число, більше
за одиницю, яке не є добутком двох натуральних чисел,
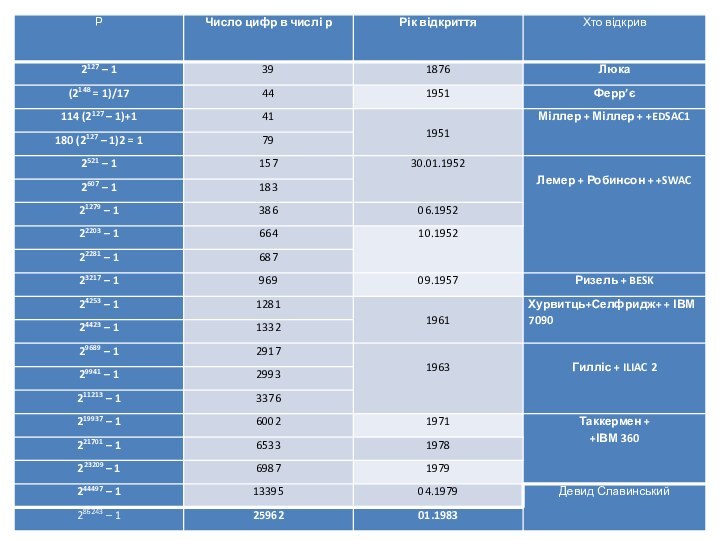
більших за одиницю.У 1876 році Люка довів, що число 2127 – 1 просте, й 75 років воно залишалося найбільшим з відомих простих чисел, що вважається не дивним, якщо подивитися на нього:
2127 – 1 =
= 170.141.183.460.231.731.687.303.715.884.105.727
Слайд 13 2, 3, 5, 7, 11, 13, 17, 19,
23, 29, 31, 37, 41, 43, 47, 53, 59,
611 2 2 4 2 4 2 4 6 2 6 4 2 4 6 6 2
1 0 2 2 2 2 2 2 4 4 2 2 2 2 0 4
1 2 0 0 0 0 0 2 0 2 0 0 0 2 4
1 2 0 0 0 0 2 2 2 2 0 0 2 2
1 2 0 0 0 2 0 0 0 2 0 2 0
1 2 0 0 2 2 0 0 2 2 2 2
1 2 0 2 0 2 0 2 0 0 0
1 2 2 2 2 2 2 2 0 0
1 0 0 0 0 0 0 2 0
1 0 0 0 0 0 2 2
Гіпотеза 1 0 0 0 0 2 0 Гільбрайта
1 0 0 0 2 2
1 0 0 2 0
1 0 2 2
1 2 0
2
1
Слайд 14
Декілька нерозв’язаних задач
2. Ми не знаємо, чи існує
нескінченна множина трійок послідовних натуральних чисел, кожне з яких
є добутком двох різних простих чисел. (Прикладом такої трійки може послужити трійка чисел: 33 = 3·11, 34 = 2·17, 35 = 5·7, а також трійка чисел: 93 = 3·31, 94 = 2·47, 95 = 5·19). Висловлено припущення, що таких трійок існує нескінченно багато.3. Ми не знаємо, чи справедлива гіпотеза А. Шинцеля, згідно якої для кожного числа x ≥ 117 існує хоча б одне просте число p, яке міститься між x та x + . Цю гіпотезу А. Шинцель перевірив для всіх чисел x таких, що
117 ≤ x < 2·107.
1. Ми не знаємо, чи існує нескінченно багато пар послідовних натуральних чисел, кожне з яких має тільки один простий дільник (як, наприклад, пари 2 і 3, 3 і 4, 4 і 5, 7 і 8, 8 і 9, 16 і 17, 31 і 32). Нам відомо тільки 26 таких пар, з яких найвищою є пара 24423 – 1 і 2442 .
Слайд 16
Район дослідження:
Швайківська ЗОШ
Об'єкти спостережень і досліджень:
учні
Швайківської ЗОШ
Предмети спостережень і досліджень:
знання учнів за
темою «Прості числа»Кількість опитаних:
27 чоловік.
Склад:
учні школи.





























