Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

Презентация на тему Дифференциальные уравнения высших порядков

Содержание

1. Общие сведения.
Глава 2. Дифференциальные уравнения высших порядков. 1. Общие сведения. Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется дифференциальным Теорема: Дано дифференциальное уравнение 2.Типы уравнений, допускающих понижение порядка. 1. 2. Дифференциальное уравнение не содержащее явно 3. Уравнение вида 4. Если левая часть уравнения есть точная правая, то порядок уравнения поднимается Линейное дифференциальное уравнение высшего порядка. Линейным дифференциальным уравнением n-го порядка называется уравнение вида: Теорема Пусть коэффициент , . Определение: Уравнение вида называется линейным однородным дифференциальным уравнением. Определение. Обозначим линейную часть уравнения через , Свойства линейного дифференциального оператора.1.Постоянный множитель можно выносить за знак оператора, то есть Определение: Линейное дифференциальное однородное уравнение можно записать в виде Теоремы о свойствах частичных решений Теорема1. Если функция является решением уравнения Теорема2. Если функции и являются решениями уравнения Теорема3. Если - частные решения Линейная зависимость и независимость функций. Определитель Вронского и его применение. Определение. Система функций определенных и непрерывных на Теорема. Если уравнение линейно зависимо, то хотя бы одну из них можно выразить через остальные. Если функции системы дифференцируемы n-1 то из них можно построить определитель n-го Теорема1.Если функции линейно зависимы, Теорема 2.Если - линейно независимые функции, Определение.Систему частных решений линейного однородного дифференциального Теорема.Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством фундаментальных систем. Теорема Если функции образуют фундаментальную систему Линейное однородное уравнение с постоянным коэффициентом. Определение. Уравнение вида Определение. называется характеристическим членом линейного однородного дифференциального уравнения. Определение. Уравнение называется характеристическим уравнением линейного однородного дифференциального уравнения. Все корни уравнения действительны и различны линейная комбинация является общим решением линейного однородного дифференциального уравнения. Все корни различны, но среди них есть комплексные формулы Эйлера : паре комплексных сопряженных корней можно поставить в соответствие частных решений Доказать самостоятельно линейную независимость системы частных решений При доказательстве нигде не учитывается, что - Вывод: Задача нахождения общего решения линейного однородного дифференциального уравнения n – го 3.Линейные неоднородные дифференциальные уравнения. Определение Линейным неоднородным дифференциальным уравнением называется уравнение вида Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения): Общее решение линейного Теорема2: Если правая часть неоднородного уравнения есть сумма двух функций, т.е.
Слайды презентации

Слайд 2 1. Общие сведения.

1. Общие сведения.

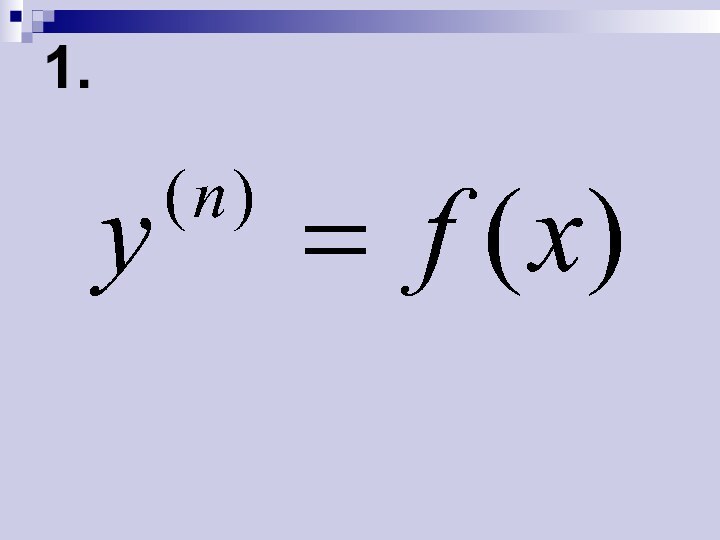
Слайд 3 Определение.
Дифференциальное уравнение содержащее производную функции двух и

Определение. Дифференциальное уравнение содержащее производную функции двух и более порядков, называется

более порядков, называется дифференциальным уравнением порядка высшее первого.
Уравнение порядка

“ ”- или

Слайд 4 Теорема:
Дано дифференциальное уравнение

Теорема: Дано дифференциальное уравнение и система

и система начальных

условий , ,…., Если функция непрерывна в окрестностях начального условия и имеет непрерывные частные производные по , то существует и притом единственное решение уравнения, определенное и непрерывное в некотором интервале содержащем , и удовлетворяющее заданной системе начальных условий.

Слайд 5 2.Типы уравнений, допускающих понижение порядка.

2.Типы уравнений, допускающих понижение порядка.

Слайд 6 1.

1.

Слайд 7 2.
Дифференциальное уравнение

2. Дифференциальное уравнение не содержащее явно и младших

не содержащее явно и младших производных до

(k-1) порядка включительно, допускает понижение порядка на k единиц

Слайд 8 3.
Уравнение вида

3. Уравнение вида также допускает

также

допускает понижение порядка путем замены обоих переменных.

Слайд 9 4.
Если левая часть уравнения есть точная правая,

4. Если левая часть уравнения есть точная правая, то порядок уравнения

то порядок уравнения поднимается на единицу путем непосредственного интегрирования.

(Это уравнение встречается редко, но к этому виду приводятся некоторые уравнения.)

Слайд 10 Линейное дифференциальное уравнение высшего порядка.

Линейное дифференциальное уравнение высшего порядка.

Слайд 11 Линейным дифференциальным уравнением n-го порядка называется уравнение вида:

Линейным дифференциальным уравнением n-го порядка называется уравнение вида:

Слайд 12 Теорема
Пусть коэффициент ,

Теорема Пусть коэффициент , . Линейное дифференциальное уравнение

. Линейное дифференциальное уравнение непрерывно на

некотором отрезке [a;b]. одно и только одно решение дифференциального уравнения, определенное и непрерывное на всем интервале (a;b), удовлетворяющее этому уравнению и любой системе начальных условий, если только значение принадлежит интервалу (a;b).

Слайд 13 Определение:
Уравнение вида

называется

Определение: Уравнение вида называется линейным однородным дифференциальным уравнением.

линейным однородным дифференциальным уравнением.

Слайд 14 Определение.
Обозначим линейную часть уравнения через

Определение. Обозначим линейную часть уравнения через ,

,

. .
Выражение называется линейным дифференциальным оператором от функции .

Слайд 15 Свойства линейного дифференциального оператора.
1.Постоянный множитель можно выносить за

Свойства линейного дифференциального оператора.1.Постоянный множитель можно выносить за знак оператора, то

знак оператора, то есть для любого n размерной дифференциальной

функции
- свойство однородности.
2.Оператор от суммы двух функций и равен сумме операторов от каждого из слагаемых в отдельности, то есть для любых n раз дифференцируемых функций и верно равенство:
- свойство аддитивности

Слайд 16 Определение:
Линейное дифференциальное однородное уравнение можно записать в

Определение: Линейное дифференциальное однородное уравнение можно записать в виде

виде

Слайд 17 Теоремы о свойствах частичных решений

Теоремы о свойствах частичных решений

Слайд 18 Теорема1.
Если функция является решением уравнения

Теорема1. Если функция является решением уравнения , то

, то и функция

есть решение этого уравнения.

Слайд 19 Теорема2.
Если функции и

Теорема2. Если функции и являются решениями уравнения

являются решениями уравнения ,

то и функция есть решение этого уравнения.

Слайд 20 Теорема3.
Если

Теорема3. Если - частные решения линейного однородного дифференциального

- частные решения линейного однородного дифференциального уравнения, то

их линейная комбинация
есть также решение этого уравнения.

Слайд 21 Линейная зависимость и независимость функций. Определитель Вронского и

Линейная зависимость и независимость функций. Определитель Вронского и его применение.

его применение.

Слайд 22 Определение.
Система функций

Определение. Система функций определенных и непрерывных на отрезке [a;b]

определенных и непрерывных на отрезке [a;b] называется линейно зависимой

на отрезке [a;b], если n таких чисел , что выполняется тождество , при этом (не все одновременно равны нулю) .

Слайд 23 Теорема.
Если уравнение линейно зависимо, то хотя бы

Теорема. Если уравнение линейно зависимо, то хотя бы одну из них можно выразить через остальные.

одну из них можно выразить через остальные.

Слайд 24 Если функции системы дифференцируемы n-1 то из них

Если функции системы дифференцируемы n-1 то из них можно построить определитель

можно построить определитель n-го порядка, который имеет вид



Этот определитель

является функцией от х и обозначается
Этот определитель называется определителем Вронского

Слайд 25 Теорема1.
Если функции

Теорема1.Если функции линейно зависимы, то определитель Вронского тождественно равен 0.

линейно зависимы, то определитель Вронского тождественно равен

0.

Слайд 26 Теорема 2.
Если

Теорема 2.Если - линейно независимые функции, удовлетворяющие некоторому

- линейно независимые функции, удовлетворяющие некоторому однородному дифференциальному уравнению

n-го порядка, то определитель системы не обращается в ноль ни в одной точке.

Слайд 27 Определение.
Систему частных решений

Определение.Систему частных решений линейного однородного дифференциального уравнения n-го

линейного однородного дифференциального уравнения n-го порядка называют фундаментальной,

если она состоит из n независимых функций.

Слайд 28 Теорема.
Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством

Теорема.Любое линейное однородное дифференциальное уравнение обладает бесчисленным множеством фундаментальных систем.

фундаментальных систем.

Слайд 29 Теорема
Если функции

Теорема Если функции образуют фундаментальную систему решений уравнения,то

образуют фундаментальную систему решений уравнения

,то их линейная комбинация

- является общим решением этого уравнения.

Слайд 30 Линейное однородное уравнение с постоянным коэффициентом.

Линейное однородное уравнение с постоянным коэффициентом.

Слайд 31 Определение.
Уравнение вида

Определение. Уравнение вида

, г де =const, называется линейным однородным дифференциальным уравнением с постоянным коэффициентом.

Слайд 32 Определение.

называется характеристическим членом линейного однородного дифференциального

Определение. называется характеристическим членом линейного однородного дифференциального уравнения.

уравнения.

Слайд 33 Определение.
Уравнение

называется характеристическим уравнением линейного однородного дифференциального

Определение. Уравнение называется характеристическим уравнением линейного однородного дифференциального уравнения.

уравнения.

Слайд 34 Все корни уравнения


действительны и различны

Все корни уравнения действительны и различны

Слайд 35
линейная комбинация


является общим решением линейного однородного дифференциального

линейная комбинация является общим решением линейного однородного дифференциального уравнения.

уравнения.

Слайд 36 Все корни различны, но среди них есть комплексные

Все корни различны, но среди них есть комплексные

Слайд 37 формулы Эйлера :

формулы Эйлера :

Слайд 38 паре комплексных сопряженных корней

можно поставить в

паре комплексных сопряженных корней можно поставить в соответствие частных решений

соответствие частных решений

Слайд 39 Доказать самостоятельно линейную независимость системы частных решений

Доказать самостоятельно линейную независимость системы частных решений

Слайд 40 При доказательстве нигде не учитывается, что

При доказательстве нигде не учитывается, что - действительное число

- действительное число поэтому когда пара

корней является двойной, то ей соответствует четыре частных решения следующих видов:

Слайд 41 Вывод:
Задача нахождения общего решения линейного однородного дифференциального

Вывод: Задача нахождения общего решения линейного однородного дифференциального уравнения n –

уравнения n – го порядка с постоянным коэффициентом сводится

к нахождению всех корней алгебраического уравнения n-ой степени.

Слайд 42 3.Линейные неоднородные дифференциальные уравнения.

3.Линейные неоднородные дифференциальные уравнения.

Слайд 43 Определение
Линейным неоднородным дифференциальным уравнением называется уравнение вида

Определение Линейным неоднородным дифференциальным уравнением называется уравнение вида

Слайд 44 Теорема (о структуре общего решения линейного неоднородного дифференциального

Теорема (о структуре общего решения линейного неоднородного дифференциального уравнения): Общее решение

уравнения):
Общее решение линейного неоднородного дифференциального уравнения представляет сумму

частного решения этого уравнения и общего решения соответствующего однородного (при g=0), .
  • Имя файла: differentsialnye-uravneniya-vysshih-poryadkov.pptx
  • Количество просмотров: 112
  • Количество скачиваний: 0
- Предыдущая Изготовление аппликаций
Следующая - Культура России в 18 веке

Похожие презентации

Методы решения иррациональных уравнений Методы решения иррациональных уравнений 106
Угол. Виды углов Угол. Виды углов 103
Формирование элементарных математических представлений у детей дошкольного возраста с использованием ПМК Мозаичный ПАРК презентация к уроку по математике (младшая, средняя, старшая, подготовительная группа) Формирование элементарных математических представлений у детей дошкольного возраста с использованием ПМК Мозаичный ПАРК презентация к уроку по математике (младшая, средняя, старшая, подготовительная группа) 148
Презентация Знакомим дошкольника с часами презентация к уроку по математике (подготовительная группа) Презентация Знакомим дошкольника с часами презентация к уроку по математике (подготовительная группа) 226
Состав чисел от 1 до 10 Состав чисел от 1 до 10 103
Действия с рациональными числами Действия с рациональными числами 95
Сфера и плоскость Сфера и плоскость 129
Десятичные дроби 6 класс Десятичные дроби 6 класс 174
Презентация +конспект урока по математике в 5 классе по теме: Презентация +конспект урока по математике в 5 классе по теме: 131
Комплексные числа - практика Комплексные числа - практика 107
Communication and signaling. (Lecture 8) Communication and signaling. (Lecture 8) 105
презентация В поисках сюрприза план-конспект занятия по математике (старшая группа) презентация В поисках сюрприза план-конспект занятия по математике (старшая группа) 99
Отношения. Пропорции.Подготовка к контрольной работе Отношения. Пропорции.Подготовка к контрольной работе 97
Презентация по математике на тему Степень числа.Квадрат и куб числа(6класс,ФГОС) Презентация по математике на тему Степень числа.Квадрат и куб числа(6класс,ФГОС) 125
Презентация: Определители и их применение Презентация: Определители и их применение 150
Презентация к уроку математики по программе Перспективная начальная школа презентация к уроку по математике (1 класс) Презентация к уроку математики по программе Перспективная начальная школа презентация к уроку по математике (1 класс) 103
Логарифмические спирали Логарифмические спирали 112
Презентация Архимед и корона царя Гиерона Презентация Архимед и корона царя Гиерона 285
okr okr 118
Презентация по математике на тему Тела вращения Презентация по математике на тему Тела вращения 103
Презентация клуба для одарённых детей (математика) презентация к уроку по математике (4 класс) по теме Презентация клуба для одарённых детей (математика) презентация к уроку по математике (4 класс) по теме 123
Презентация к уроку МАТЕМАТИКИ. ТЕМА : Задачи с недостающими данными (путешествие по рекам Ленинградской области) Презентация к уроку МАТЕМАТИКИ. ТЕМА : Задачи с недостающими данными (путешествие по рекам Ленинградской области) 142
Умножение одночленов. Возведение одночлена в степень Умножение одночленов. Возведение одночлена в степень 120
Урок математики В царстве смекалки презентация к уроку по математике (3 класс) Урок математики В царстве смекалки презентация к уроку по математике (3 класс) 150
презентация Организм человека презентация к уроку по математике (3 класс) презентация Организм человека презентация к уроку по математике (3 класс) 113
Презентация по математике на тему Тригонометрия Презентация по математике на тему Тригонометрия 123
Известные имена. Софья Ковалевская Известные имена. Софья Ковалевская 91
Занимательные задачи в стихах презентация к уроку по математике (3 класс) Занимательные задачи в стихах презентация к уроку по математике (3 класс) 257
Презентация Конкурс-викторина Звездный час Презентация Конкурс-викторина Звездный час 110
Измерение времени Измерение времени 119