Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть 

Яндекс.Метрика

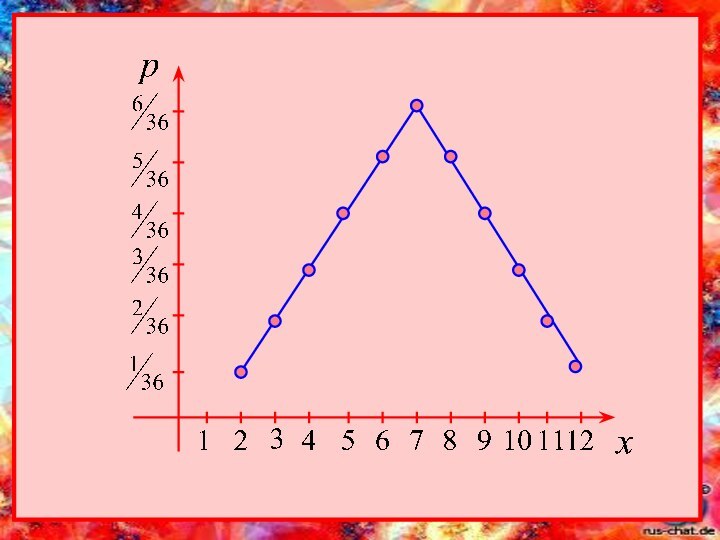
Презентация на тему Дискретные случайные величины

Содержание

Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Х - число очков, выпавших при бросании кубика. Х - случайная величина и множество ее значений будет: {1,2,3,4,5,6}
Случайной величиной называется величина, которая в результате опыта принимает заранее неизвестное численное Будем обозначать случайные величины Х, а их возможные значения х. Например, пусть Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е. все Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет собой Поскольку ряд распределения содержит все возможные значения случайной величины, то суммарная вероятность ПРИМЕР.Рассмотрим опыт с бросанием двух игральных кубиков. Пусть случайная величина Х - Р(X10)=P(X=11)+P(X=12)==2/36+1/36=3/36=1/12P(3
Слайды презентации

Слайд 2
Будем обозначать случайные величины Х, а их возможные

Будем обозначать случайные величины Х, а их возможные значения х. Например,

значения х.
Например, пусть Х - число очков, выпавших

при бросании кубика. Х - случайная величина и множество ее значений будет:

{1,2,3,4,5,6}

Слайд 3
Случайная величина называется дискретной,
если множество ее возможных

Случайная величина называется дискретной, если множество ее возможных значений cчетно (т.е.

значений
cчетно (т.е. все возможные значения
можно пронумеровать натуральными


числами)
{x1 ,x2 ,…,xn }

Слайд 4
Дискретная случайная величина полностью определяется своим рядом распределения.

Дискретная случайная величина полностью определяется своим рядом распределения. Ряд распределения представляет


Ряд распределения представляет собой
таблицу, в которой указаны
все

возможные значения случайной
величины и их вероятности:

Слайд 5
Поскольку ряд распределения содержит все возможные значения случайной

Поскольку ряд распределения содержит все возможные значения случайной величины, то суммарная

величины, то суммарная вероятность должна быть равна 1.
По

ряду распределения можно находить различные вероятности и строить многоугольник распределения.

Многоугольник распределения – ломаная,
которая соединяет точки, абсциссы которых
содержит первая строка ряда распределения
(значения случайной величины),
а ординаты – вторая строка (вероятности
этих значений).

Слайд 6
ПРИМЕР.
Рассмотрим опыт с бросанием двух игральных кубиков. Пусть

ПРИМЕР.Рассмотрим опыт с бросанием двух игральных кубиков. Пусть случайная величина Х

случайная величина Х - сумма выпавших очков. Составим для

нее ряд распределения:

Найдем вероятность следующих событий:
Р(X<5), P(X>10), P(3

Слайд 7
Р(X10)=P(X=11)+P(X=12)=
=2/36+1/36=3/36=1/12

P(3

Р(X10)=P(X=11)+P(X=12)==2/36+1/36=3/36=1/12P(3
  • Имя файла: diskretnye-sluchaynye-velichiny.pptx
  • Количество просмотров: 194
  • Количество скачиваний: 0
- Предыдущая Экологический патруль по профилактике пожарной безопасности в сосновом бору
Следующая - Транспорт будущего

Похожие презентации

Л. Эйлер Л. Эйлер 109
Логарифмическая функция Логарифмическая функция 157
Математика 5 класс Входной контроль Математика 5 класс Входной контроль 164
Виды треугольников 3 класс Виды треугольников 3 класс 212
Презентаия Прибавление и вычитания числа 3 презентация к уроку по математике (1 класс) Презентаия Прибавление и вычитания числа 3 презентация к уроку по математике (1 класс) 119
Кто хочет стать математиком? Кто хочет стать математиком? 140
Решение задач по теории вероятностей Решение задач по теории вероятностей 112
Объём наклонной призмы Объём наклонной призмы 99
Аннотация Аннотация 129
ФАЛЕС МИЛЕТСКИЙ ФАЛЕС МИЛЕТСКИЙ 104
Технологическая карта урока математики Задачи на нахождение неизвестного третьего слагаемого 2 класса УМК Школа России план-конспект урока по математике (2 класс) Технологическая карта урока математики Задачи на нахождение неизвестного третьего слагаемого 2 класса УМК Школа России план-конспект урока по математике (2 класс) 229
Периметр прямоугольника. Закрепление изученного материала. (март 2019 год) методическая разработка по математике (2 класс) Периметр прямоугольника. Закрепление изученного материала. (март 2019 год) методическая разработка по математике (2 класс) 130
Урок математики в 4 классе по теме : Понятие о действии возведения в степень план-конспект урока по математике (4 класс) Урок математики в 4 классе по теме : Понятие о действии возведения в степень план-конспект урока по математике (4 класс) 106
Арифметические действия. презентация урока для интерактивной доски по математике (4 класс) по теме Арифметические действия. презентация урока для интерактивной доски по математике (4 класс) по теме 103
открытое занятие число 10 план-конспект занятия по математике (старшая группа) открытое занятие число 10 план-конспект занятия по математике (старшая группа) 124
Симметрия Симметрия 145
Презентация Буквенные выражения презентация к уроку по математике (2 класс) по теме Презентация Буквенные выражения презентация к уроку по математике (2 класс) по теме 108
Нахождение числа по его дроби У-2 Нахождение числа по его дроби У-2 103
Устный счёт презентация к уроку по математике (2 класс) по теме Устный счёт презентация к уроку по математике (2 класс) по теме 104
Решение тригонометрических уравнений Решение тригонометрических уравнений 94
Выступление на педсовете с презентацией Занимательный материал поФЭМП в подготавительной группе презентация к уроку по математике (подготовительная группа) по теме Выступление на педсовете с презентацией Занимательный материал поФЭМП в подготавительной группе презентация к уроку по математике (подготовительная группа) по теме 146
Открытый урок по математике в 1 классе по теме Число 6. Цифра 6 УМК Планета знаний план-конспект урока по математике (1 класс) Открытый урок по математике в 1 классе по теме Число 6. Цифра 6 УМК Планета знаний план-конспект урока по математике (1 класс) 98
Математические задачи Математические задачи 104
Презентация к уроку математики Математика и летние каникулы Презентация к уроку математики Математика и летние каникулы 124
Танграм Танграм 108
Число 1 Число 1 93
Урок по теме Решение уравнений Урок по теме Решение уравнений 109
Ромб Ромб 192
Образовательная деятельность по математике Путешествие Колобка в подготовительной к школе группе. план-конспект занятия по математике (подготовительная группа) по теме Образовательная деятельность по математике Путешествие Колобка в подготовительной к школе группе. план-конспект занятия по математике (подготовительная группа) по теме 135
Контрольные работы методическая разработка по математике (2 класс) по теме Контрольные работы методическая разработка по математике (2 класс) по теме 121