известно, что слово «граф» означает дворянский титул, например, граф
Лев Николаевич Толстой. А вот в математике …Граф – это конечная совокупность вершин,
некоторые из которых соединены ребрами.
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


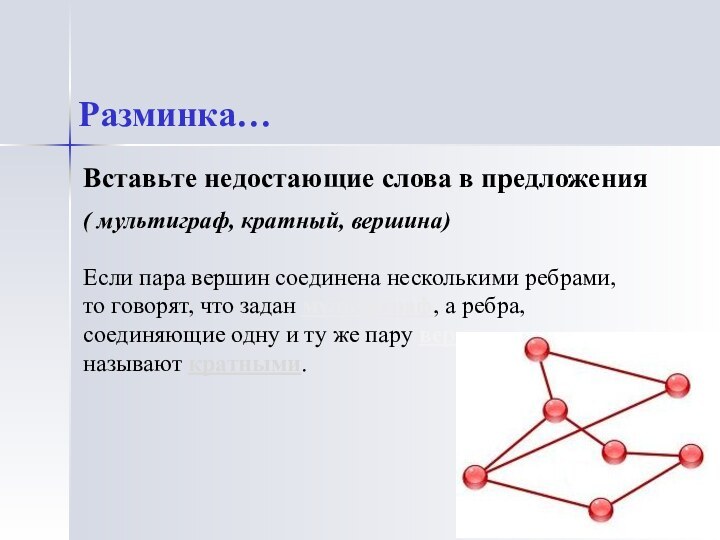









Вставьте недостающие слова в предложения
( мультиграф, кратный, вершина)
Разминка…
Разминка…
Вставьте недостающие слова в предложения
( смежный, петля)
Домашняя задачка
Условие
Домашняя задачка
Задания
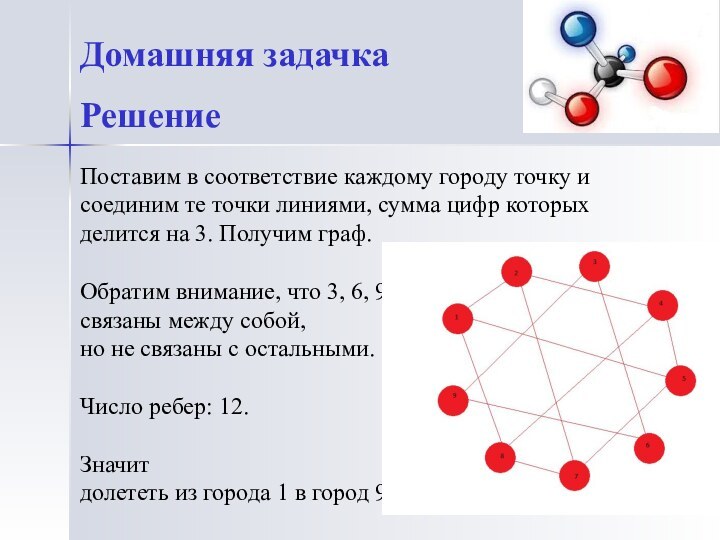
Домашняя задачка
Решение
Степень вершины графа
Степень вершины графа
Подсчет числа ребер графа
Подсчет числа ребер графа