- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дроби в музыке
Содержание
- 2. «Математика и музыка
- 3. Цель работыДоказать связи между музыкой и дробями.
- 4. Задачи исследования:♫ изучить историю возникновения дробей;♫ изучить
- 5. Необходимость в дробных числах возникла в результате
- 6. Дробина усиДроби на Руси называли ДОЛЯМИ,Позже ЛОМАННЫМИ ЧИСЛАМИ.В старых руководствах находили следующие названия дробей…
- 7. -Половина, полтина-Треть-Четь-Пятина-Полтреть-Седьмина-Полчеть- Десятина-Пол-полтреть-Пол-полчетьПол-пол-треть (малая)
- 8. Что же такое дробь в математике?
- 9. Из истории возникновения музыки Еще при первобытном
- 10. Из истории возникновения музыки В Древней Греции
- 11. Из истории возникновения музыки Пифагор (ок.
- 12. «Число правит миром»Пифагорейцы верили, что в числовых
- 13. Математика и музыка.Какая связь может существовать между этими понятиями?И существует ли эта связь вообще?
- 14. Ритм в музыке Ритм – один из
- 15. Пропорции Шестнадцатая, восьмая, четвертная, половинная, целая
- 16. Нотные равенстваДействия с дробями1/8 +
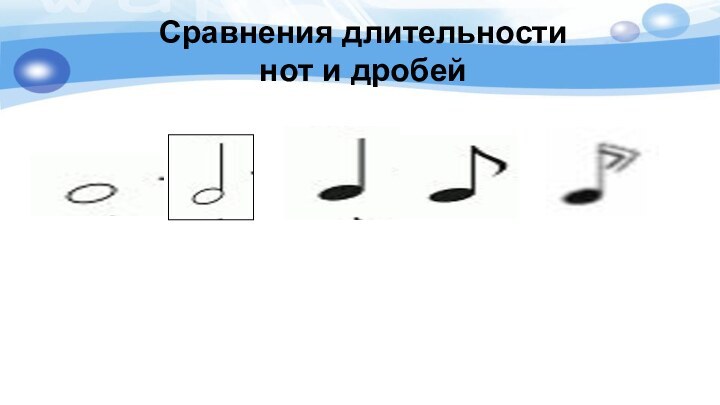
- 17. Сравнения длительности нот и дробей
- 18. Анализ и обработка отрывков музыкальных произведений В
- 19. Фрагмент русской народной песни «Ах вы, сени, мои сени»Нотная грамотаЗапись математических вычислений
- 20. Да и поныне сельские строители и плотники,
- 21. Две ноты
- 22. ПерспективаМатематика и архитектураМатематика и живописьМатематика и литератураДроби в танце так важны – с математикой дружны!
- 23. .354Выводыдлительность нот совпадает с двоичными дробями; с
- 24. Скачать презентацию
- 25. Похожие презентации























Слайд 4
Задачи исследования:
♫ изучить историю возникновения дробей;
♫ изучить историю
возникновения музыки;
♫ найти общие элементы в математике и в
музыке;♫ выявить присутствие дробей в музыкальных произведениях;
♫ проанализировать и обработать отрывок музыкального произведения, используя музыкальную грамоту;
♫ подсчитать целые и его части музыкального произведения.
Слайд 5 Необходимость в дробных числах возникла в результате практической
деятельности человека.
Потребность в нахождении долей единицы появилась
у наших предков при дележе добычи после охоты.Второй существенной причиной появления дробных чисел следует считать измерение величин при помощи выбранной единицы измерения.
Слайд 6
Дроби
на
уси
Дроби на Руси называли ДОЛЯМИ,
Позже ЛОМАННЫМИ ЧИСЛАМИ.
В
старых руководствах находили
следующие названия дробей…
Слайд 7
-Половина, полтина
-Треть
-Четь
-Пятина
-Полтреть
-Седьмина
-Полчеть
- Десятина
-Пол-полтреть
-Пол-полчеть
Пол-пол-треть (малая)
Слайд 9
Из истории возникновения музыки
Еще при первобытном строе,
на заре человеческого общества музыка играла очень важную роль.
Матери, напевая, укачивали детей, воины устрашали врагов воинственными песнями – кличами, пастухи протяжными зовами собирали стада. Если из племени кто-то умирал, то его провожали песней-плачем. Музыка входила в игры первобытных людей. Люди постепенно учились отбирать из множества шумов музыкальные звуки, научились их связывать между собой. Музыка первобытных людей была довольно простая, но в то же время с довольно сложным ритмом, который помогал найти им ритмы в работе
Слайд 10
Из истории возникновения музыки
В Древней Греции музыка
звучала в театральных представлениям, даже стихи поэты декламировали словно
песню, аккомпанируя себе на лире или кифаре. Обучение музыкальному искусству считалось обязательным для воспитания и образования гражданина (теория, пение, игра на музыкальных инструментах). Музыка в Древней Греции являлась важнейшим средством воздействия на нравственный мир человека. Здесь зародились такие понятия как мелодия, гармония, ритм, хор, оркестр, рапсодия, симфония. Музыка всегда сопровождала все спортивные соревнования, а также Олимпийские игры
Слайд 11
Из истории возникновения музыки
Пифагор
(ок. 570- ок.
550 гг. до н.э.)
Древнегреческий философ Пифагор, один из самых
первых установил связь между музыкой и математикой: создал учение о звуке,
изучал философскую математическую стороны звука,
пытался связать музыку с астрономией.
Слайд 12
«Число правит миром»
Пифагорейцы верили, что в числовых закономерностях
спрятана тайна мира.
Пифагор открыл, что основные гармонические интервалы, т.е.
октава, чистая квинта и чистая кварта, возникают, когда длины колеблющихся струн относятся как 1:2,2:3,3:4 1 1/2 1/4 1/8 1/16
Слайд 13
Математика и музыка.
Какая связь может существовать между этими
понятиями?
И существует ли эта связь вообще?
Слайд 14
Ритм в музыке
Ритм – один из важнейших
элементов музыки. Ритм – чередование длительностей.
От правильно подобранного ритма зависит звучание мелодии.
Слайд 15
Пропорции
Шестнадцатая, восьмая, четвертная, половинная, целая нота
… Названия длительностей служат одновременно и названиями чисел. В
самом деле:длительность соответствует и дробь 1/16, называются одинаково. Перечень совпадений можно продолжить.
Это равенство следует понимать в том смысле, что длительность слева равна суммарно длительности справа. С помощью чисел то же равенство можно записать в виде 1=1/4+1/4+1/2.
Слайд 16
Нотные равенства
Действия с дробями
1/8 + 1/8
= 1/4
1/4 + 1/4 = 1/2
1 - 1/2 =
1/2
От целой ноты уберем
получится
=
=
Слайд 18
Анализ и обработка отрывков музыкальных произведений
В представленных
произведениях просчитаем общую
длительность всех нот входящих в каждый
тактНетрудно заметить, что в каждом такте любого произведения получили одни и те же числа.
Это число называется размером музыкального произведения и записывается в начале нотного стана.
Слайд 19
Фрагмент русской народной песни
«Ах вы, сени, мои
сени»
Нотная грамота
Запись математических вычислений
Слайд 20 Да и поныне сельские строители и плотники, закладывая
фундамент избы, изготовляя ее детали, вычерчивают этот треугольник, чтобы
получить прямой угол.
Слайд 21
Две ноты -
два слога,
А слово - одно,
И меру длиныОзначает оно.
(Ми + Ля = Миля)
Первую в школе все изучают,
Ну а второй из двустволки стреляют.
Третью исполнят нам два барабана
Иль каблуки отобьют её рьяно.
(Дробь)
Первый слог - нота,
Второй слог - нота.
А в целом -
Только часть чего-то.
(До + Ля = Доля)
Слайд 22
Перспектива
Математика и архитектура
Математика и живопись
Математика и литература
Дроби в
танце так важны –
с математикой дружны!
Слайд 23
.
3
5
4
Выводы
длительность нот совпадает с двоичными дробями;
с длительностями
нот можно выполнять действия сложения и вычитания, так же
как и с дробями;длительности нот и дроби можно сравнивать.