и ограниченная область на плоскости XOY и в ней
определена произвольная ограниченная функция z=f(x,y).Разобьем область D сетью кривых на n произвольных частей Di с площадями ΔSi.
В каждой из областей Di выберем точку (ξi,ηi).
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


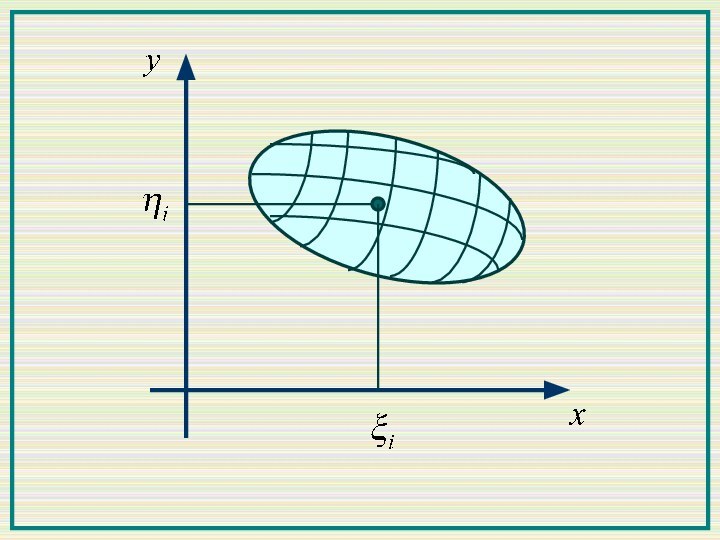



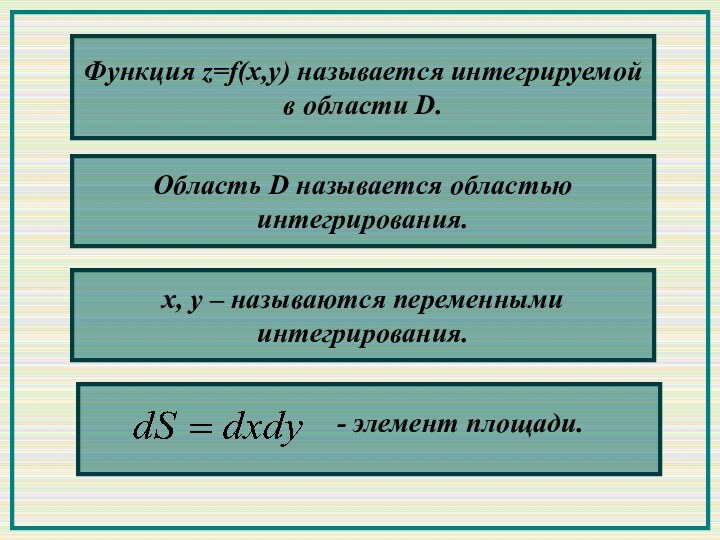

Интегральная сумма зависит от способа разбиения отрезка и выбора точек (ξi, ηi).