Презентация на тему Эконометрика. Модель парной и множественной линейной регрессии

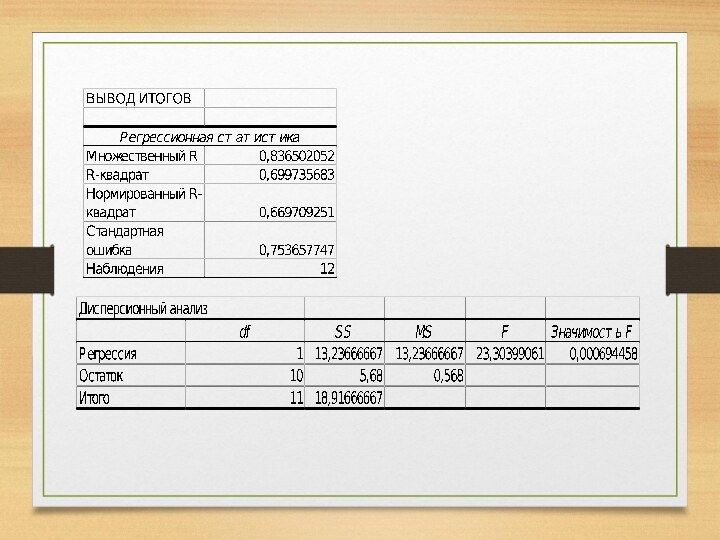
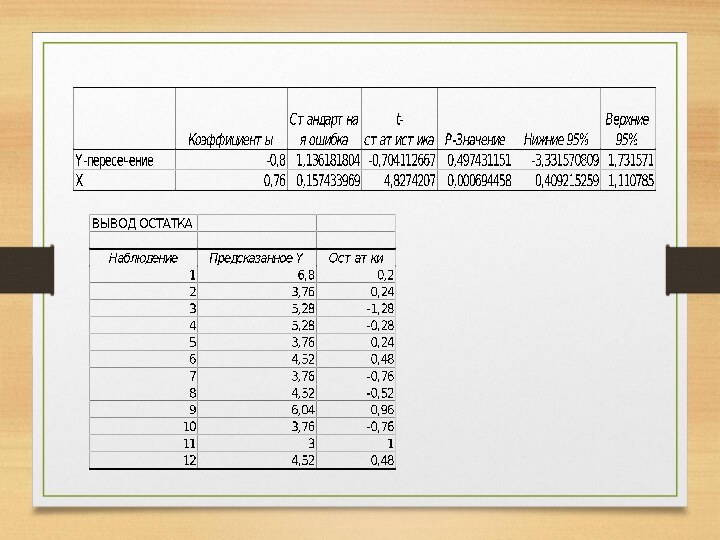
регрессии
3. Итоговый коллоквиум
4. Итоговая контрольная работа
5. Модель временного

ряда
6. Презентация

5

10

10

5

10

10

на базе реальных статистических данных
строятся,
анализируются и
совершенствуются

математические модели реальных экономических явлений.

модель относится классу математических моделей.
Модели экономических объектов, создаваемые

именно в эконометрике, являются дескриптивными (описывающими реальность такой, как она есть, в отличие от оптимизационных моделей).

между которыми нас интересуют;
априорный, предмодельный анализ содержательной сущности моделируемого

явления;
информационно-статистический этап – получение данных, анализ их качества;
этап спецификации модели;
этап параметризации модели – определяем вид эконометрической модели, выражаем в математической форме взаимосвязь между её переменными, формулируем исходные предпосылки и ограничения модели.
этап идентификации модели – статистический анализ модели, оценка качества её параметров по имеющимся статистическим данным;
этап верификации модели, анализа её точности и адекватности;
интерпретация полученных результатов.

одним уравнением

Модели временных рядов

Системы

одновременных уравнений

одного показателя соответствует строго определенное значение другого.
Статистической (стохастической,

вероятностной) называется взаимосвязь, при которой одному значению первого показателя может соответствовать несколько значений второго показателя.
Среди статистических зависимостей наибольший интерес представляют корреляционные зависимости.
Корреляционная зависимость заключается в том, что средняя величина одного показателя изменяется в зависимости от значения другого.
Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условным математическим ожиданием (средним значением) другой.

сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры выборочного уравнения

линейной регрессии с помощью МНК.
3. Оцените тесноту связи с помощью показателей корреляции (выборочный коэффициент корреляции) и детерминации.
4. Используя критерий Стьюдента оцените статистическую значимость коэффициентов регрессии и корреляции.
5. Постройте интервальные оценки параметров регрессии. Проверьте, согласуются ли полученные результаты с выводами, полученными в предыдущем пункте.

оценки значимости уравнения в целом.
7. С помощью теста Гольдфельда –

Квандта исследуйте гетероскедастичность остатков. Сделайте выводы.
8. В случае пригодности линейной модели рассчитайте прогнозное значение результата, если значение фактора увеличится на 5% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости =0,05.
9. Оцените полученные результаты, проинтерпретируйте полученное уравнение регрессии.

коэффициент корреляции) и детерминации
Коэффициент корреляции

признака Y, объясняемую регрессией, в общей дисперсии результативного признака.

Соответственно величина 1- R2 характеризует долю дисперсии Y, вызванную влиянием остальных, не учтенных в модели факторов.
Коэффициент детерминации
R2 = rxy2

и корреляции
Н 0 : b1 = 0
Н 1: b1

≠ 0

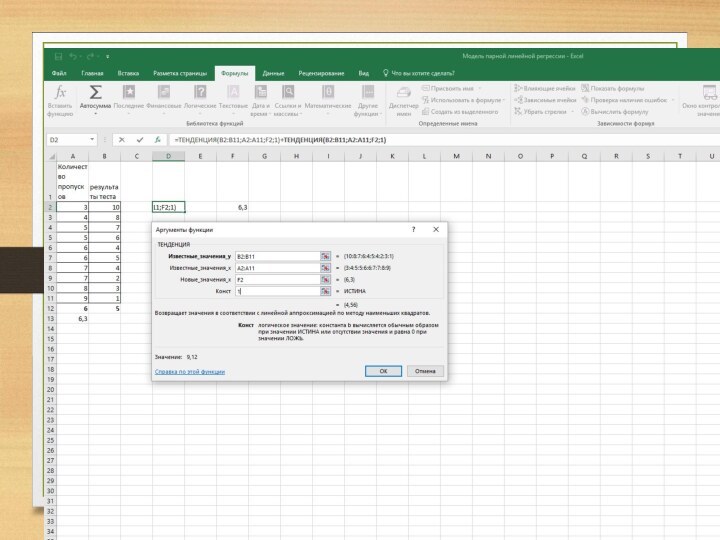
Статистика критерия при нулевой гипотезе имеет
распределение Стьюдента с (n-2) степенями свободы

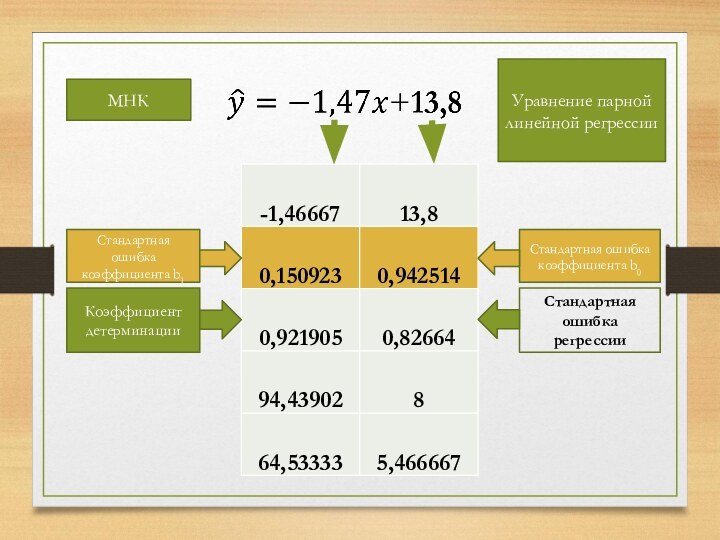
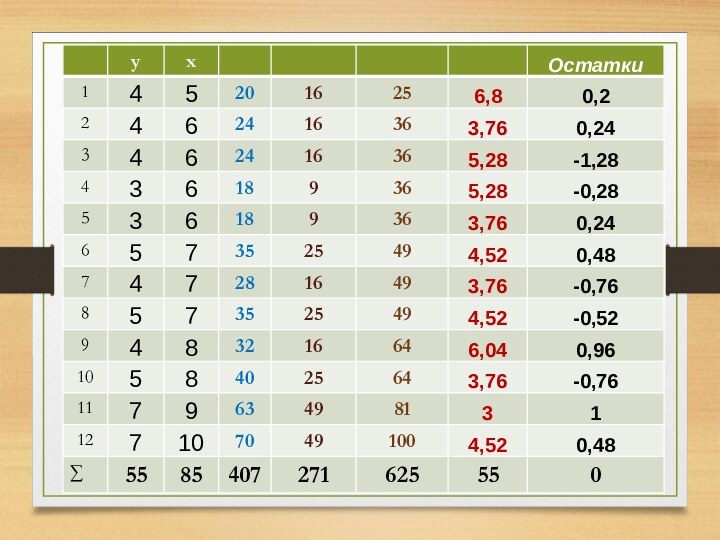
Стандартная ошибка коэффициента регрессии

Несмещенная оценка дисперсии случайных отклонений

при заданном уровне значимости α больше критического (табличного) t

табл , т.е.
|tфакт| > t табл = t(α ; n-2),
то гипотеза Н 0 : b1 = 0, отвергается в пользу альтернативной при выбранном уровне значимости. Это подтверждает статистическую значимость коэффициента регрессии b1.

b1

Стандартная ошибка коэффициента b0

связи
Пусть имеется два ряда эмпирических данных
X (x1, x2,

…, xn) и
Y (y1, y2, …, yn), соответствующие им точки с координатами (xi, yi), где i=1,2,…,n, отобразим на координатной плоскости. Такое изображение называется
полем корреляции.

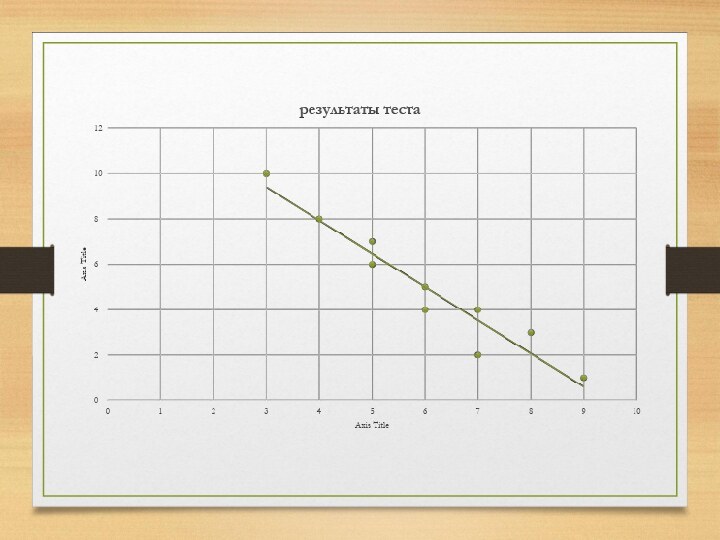
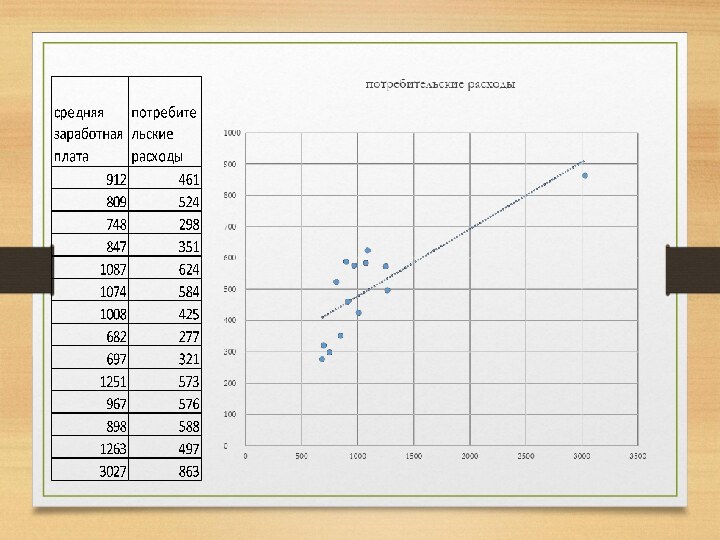
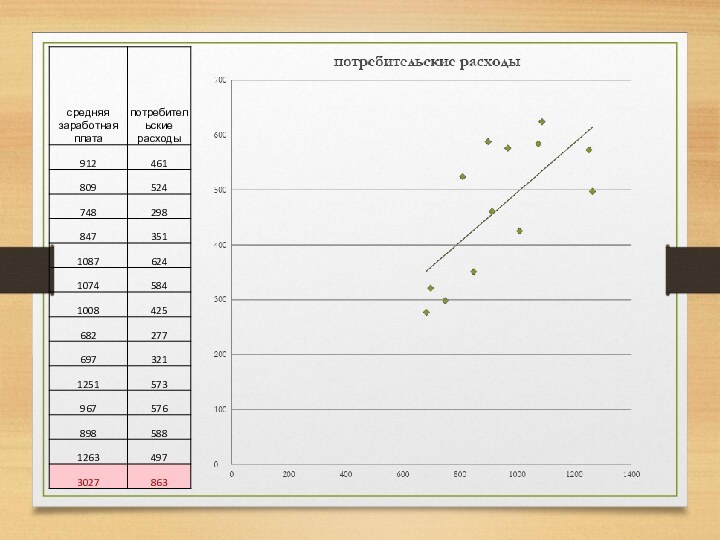
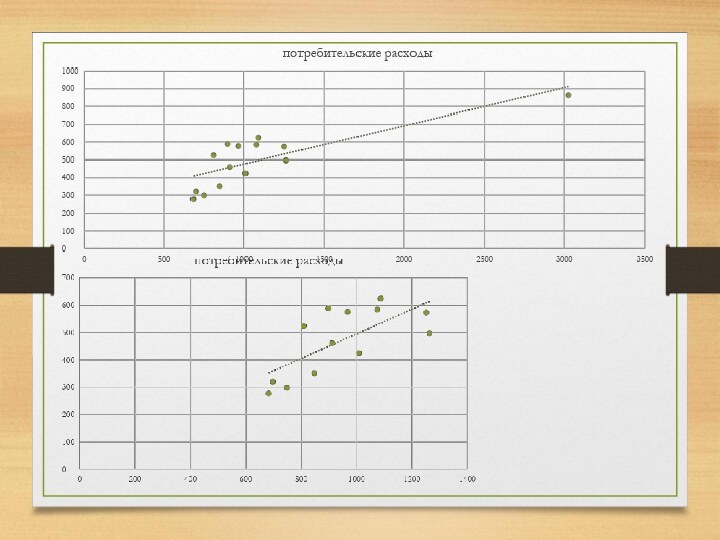
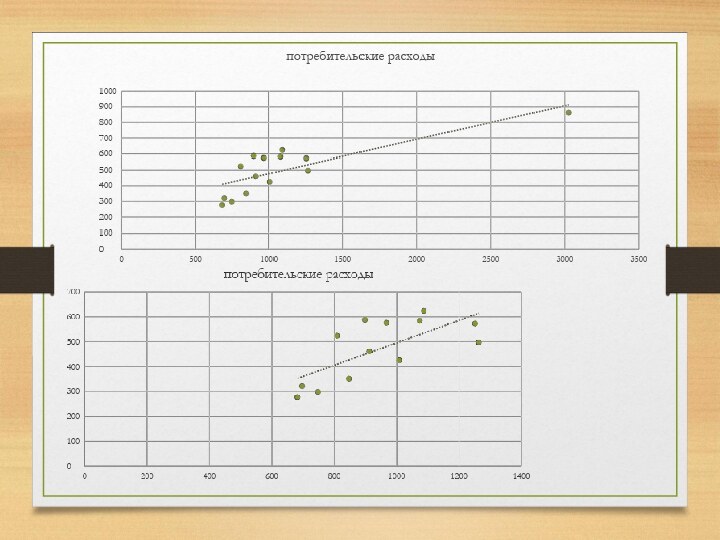
Визуальный анализ корреляционного поля позволяет сделать предположение о форме взаимосвязи двух исследуемых показателей.
По форме взаимосвязи корреляционные зависимости принято разделять на линейные и нелинейные.