- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Это загадочное число Пи
Содержание
- 2. Знаете ли вы, что эта обыкновенная, на
- 3. Неофициальный праздник «День числа Пи» (англ. Pi
- 4. Если принять диаметр окружности за единицу, то длина окружности — это число π.
- 5. Запомни, что =
- 6. История числа Пи
- 7. Проблеме π – 4000 лет. Исследователи древних
- 8. В Вавилоне в V в. до н.э.
- 9. Архимед (III в. до н.э.) для оценки
- 10. Индусы в V – VI пользовались числом
- 11. В XV веке иранский математик Аль-Каши нашёл
- 12. А голландский вычислитель – Лудольф Ван-Цейлен (1540
- 13. Обозначение π (первая буква в греческом слове
- 14. Различные способывычисления числа π
- 15. Библейское вычисление числа π
- 16. Одно из ранних приближений для числа π
- 17. Это культовое сооружение украшал большой бассейн для
- 18. Если диаметром этого сосуда было 10 локтей,
- 19. Длина диаметра в 10 локтей является длиной
- 20. Экспериментальное определение числа пи.
- 21. Дано: L = 30 локтя, D =
- 22. Итак, систематическая погрешность измерений равнаОценим относительную погрешность
- 23. Значение числа пи, известное нам сейчас с
- 24. В Библии не содержится ни одной ошибки.
- 25. Начертим на плотном картоне окружность диаметра
- 26. Следуя данным рекомендациям, мы выполнили измерения и вычислили число . Получили результаты представленные в таблице:Простейшие вычисления
- 27. Измерение с помощью взвешивания На листе картона
- 28. Измерение с помощью взвешивания Определим массу
- 29. Суммирование площадей прямоугольников, вписанных в полукруг.
- 30. Программа 10 REM *** ВЫЧИСЛЕНИЕ p***20
- 31. Полученные значения числа записаны в таблице Суммирование площадей прямоугольников, вписанных в полукруг.
- 32. Метод Монте-Карло Это фактически метод статистических
- 33. Метод Монте-КарлоДля опыта приготовим кусок картона, нарисуем
- 34. Метод Монте-КарлоПодсчитаем число следов внутри квадрата и
- 35. Применение метода Монте-Карло стало возможным только благодаря
- 36. Полученные значения числа записаны в таблице
- 37. Вычисление с помощью ряда ТейлораОбратимся к рассмотрению
- 38. Вычисление с помощью ряда ТейлораПрограммаREM "Вычисление пи"REM
- 39. Вычисление с помощью ряда Тейлора
- 40. Скачать презентацию
- 41. Похожие презентации
Знаете ли вы, что эта обыкновенная, на первый взгляд, полузабытая буква из школьного курса геометрии намного интереснее при ближайшем рассмотрении и изучении, имеет свою историю, очень много значит для математиков — они без неё просто никуда,





































Слайд 3
Неофициальный праздник «День числа Пи»
(англ. Pi Day)
отмечается 14 марта, которое в американском формате дат записывается
как 3.14, что соответствует приближённому значению числа π.Слайд 7 Проблеме π – 4000 лет. Исследователи древних пирамид
установили, что частное, полученное от деления суммы двух сторон
основания на высоту пирамиды, вырабатывается числом 3,1416. В знаменитом папирусе Ахмеса приводится такое указание для построения квадрата, равного по площади кругу: «Отбрось от диаметра его девятую часть и построй квадрат со стороной, равной остальной части, будет он эквивалентен кругу». Из этого следует, что у Ахмеса π ≈ 3,1605. Так началась письменная история π.Слайд 8 В Вавилоне в V в. до н.э. пользовались
числом 3,1215, а в Древней Греции числом (
) ≈ 3,1462643. В индийских «сутрах» VI – V в. до н.э. имеются правила, из которых вытекает, что π = 3,008. Наиболее древняя формулировка нахождения приблизительного значения отношения длины окружности к диаметру содержится в стихах индийского математика Аршабхата (V – VI в.):Прибавь четыре к сотне и умножь на восемь,
Потом ещё шестьдесят две тысячи прибавь,
Как поделить результат на двадцать тысяч,
Тогда откроется тебе значение
Длины окружности к двум радиусам отношенья
т.е. =
Слайд 9 Архимед (III в. до н.э.) для оценки числа
π вычислял периметры вписанных и описанных многоугольников от шести
до 96-ти. Такой метод вычисления длины окружности посредством периметров вписанных и описанных многоугольников применялся многими видными математиками на протяжении почти 2000 лет. Архимед получил:, т.е. π ≈ 3,1418
Долгое время все пользовались значением числа, равным
Слайд 10 Индусы в V – VI пользовались числом 3,1611,
а китайцы - числом 3,1415927; это значение записывалось
в виде именованного числа:3 чжана 1 чи 4 цуня 1 фень 5 ме 9 хао 2 мяо 7 хо.
Слайд 11 В XV веке иранский математик Аль-Каши нашёл значение
π с 16-ю верными знаками, рассмотрев вписанный и описанный
многоугольники с 80.035.168 сторонами.Андриан Ван Ромен (Бельгия) в XVI в. с помощью 230-угольников получил 17 верных десятичных знаков
Слайд 12 А голландский вычислитель – Лудольф Ван-Цейлен (1540 –
1610), вычисляя π, дошёл до многоугольников с 602 029
сторонами, и получил 35 верных знаков для π. Учёный обнаружил большое терпение и выдержку, несколько лет затратив на определение числа π. В его честь современники назвали π – «Лудольфово число». Согласно завещанию на его надгробном камне было высечено найденное им значение π.Слайд 13 Обозначение π (первая буква в греческом слове –
окружность, периферия) впервые встречается у английского математика Уильяма Джонсона
(1706 г.), а после опубликования работы Леонарда Эйлера(1736 г. Санкт-Петербург), вычислившего значение π с точностью до 153 десятичных знаков, обозначение π становится общепринятым.
Уильям Джонсон
Леонард Эйлер
Слайд 16 Одно из ранних приближений для числа π можно
извлечь из канонического текста Библии, датируемого примерно X-V веками
до нашей эры. В третьей книге Царств подробно рассказывается о том, как мастер Хирам сооружал по заказу правителя Иудейского Израильского царства Соломона храм.Царь Соломон, держащий в руках изображение храма
Слайд 17 Это культовое сооружение украшал большой бассейн для омовения
священнослужителей под названием «медного моря»: «И сделал литое из
меди море, - от края его до края его десять локтей, - совсем круглое, вышиною в пять локтей, и снурок в тридцать локтей обнимал его кругом.» (Третья книга Царств. Гл. 7, стих 23.)Слайд 18 Если диаметром этого сосуда было 10 локтей, тогда
длина окружности должна была быть 31,415926… локтей, а не
просто 30 локтей как написано в библии! Любой школьник может сказать вам, что длину окружности круга можно найти, умножив диаметр на пи. Эта явная математическая ошибка заставила нас, как христиан, сомневаться в точности Библии.Слайд 19 Длина диаметра в 10 локтей является длиной от
наружного обода до наружного обода, так, как любой человек
и будет измерять круглый предмет. Окружность длиной в 30 локтей, однако, является внутренним кругом, после вычитания толщины меди (две ладони одна на каждую сторону), из которой был сделан сосуд. Это и будет необходимым числом для вычисления объема воды.
Слайд 20
Экспериментальное определение числа пи. Погрешность измерения.
Воспримем этот
текст как древний опыт по экспериментальному определению числа пи
и на основании данных оценим погрешность измерения.Формула для измерения очевидна:
где L - длина окружности,
а D - её диаметр.
Слайд 21 Дано: L = 30 локтя, D = 10
локтей.
Из написания видно, что абсолютные погрешности каждой из величин
составляют не менее 0,5 локтя. Мы тем самым берём половину последней значащей цифры, если считать, что каждое из чисел имеет две значащие. Вариант, что погрешность измерения была больше, обсудим в конце вычислений. Рассчитаем измеренное число пи
Слайд 22
Итак, систематическая погрешность измерений равна
Оценим относительную погрешность измерения
числа пи как среднеквадратичное от относительных погрешностей данных величин:
Рассчитаем
абсолютную погрешность измерения с учётом этой формулы следовательно ответ записывается в виде
Слайд 23 Значение числа пи, известное нам сейчас с огромной
точностью, вполне укладывается в ответ, полученный экспериментально несколько тысяч
лет назад. Выходит, что если рассуждать не поверхностно, а с точки зрения методов науки, противоречия между текстом Писания и действительностью нет.Слайд 24 В Библии не содержится ни одной ошибки. Кстати,
Соломон сделал это открытие тысячу лет до нашей эры,
задолго до того как греки снова нашли число пи.Слайд 25 Начертим на плотном картоне окружность диаметра d
(15 см), вырежем получившийся круг и обмотаем вокруг него
тонкую нить. Измерив длину L (46,5 см) одного полного оборота нити, разделим L на длину диаметра окружности. Получившееся частное будет приближенным значением числа π, т.е. π = , π = 46,5 см / 15 см.π = 3,1. Данный довольно грубый способ даёт в обычных условия приближённое значение числа
π с точностью до 1.
Простейшие вычисления
Слайд 26 Следуя данным рекомендациям, мы выполнили измерения и вычислили
число . Получили результаты представленные в таблице:
Простейшие вычисления
Слайд 27
Измерение с помощью взвешивания
На листе картона начертим квадрат.
Впишем в него круг. Вырежем квадрат. Вырежем из квадрата
круг.
Слайд 28
Измерение с помощью взвешивания
Определим массу картонного
квадрата с помощью школьных весов. Взвесим круг. Зная массы
квадрата mкв (10 г) и вписанного в него круга mкр (7,8 г), воспользуемся формулами m=rV, V=Sh, где r и h-соответственно плотность и толщина картона, S-площадь фигуры. Рассмотрим равенства: mкв = r S кв h = r 4 R2 h,mкр = r Sкр h = r π R2 h.
Отсюда mкр : mкв = π : 4, π = 4 mкр : mкв.
Слайд 29
Суммирование площадей прямоугольников,
вписанных в полукруг.
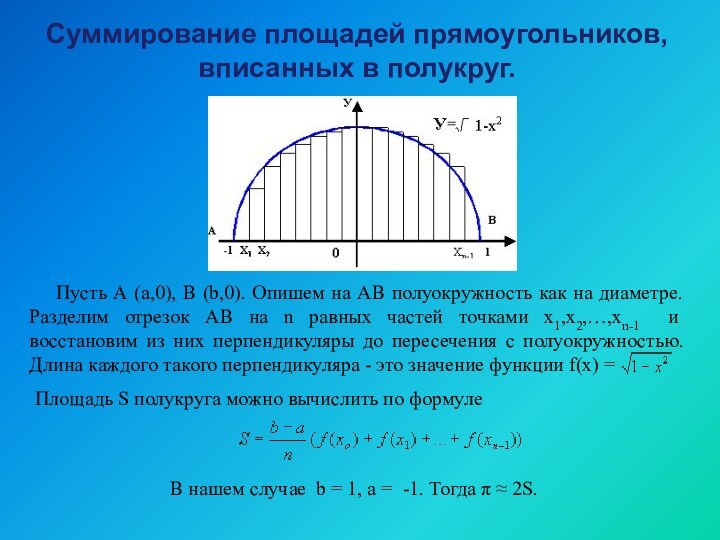
Пусть А (а,0), В (b,0). Опишем на АВ полуокружность
как на диаметре. Разделим отрезок АВ на n равных частей точками х1,х2,…,хn-1 и восстановим из них перпендикуляры до пересечения с полуокружностью. Длина каждого такого перпендикуляра - это значение функции f(x) =Площадь S полукруга можно вычислить по формуле
В нашем случае b = 1, a = -1. Тогда π ≈ 2S.
Слайд 30
Программа
10 REM *** ВЫЧИСЛЕНИЕ p***
20 REM ***
МЕТОД ПРЯМОУГОЛЬНИКОВ ***
30 INPUT N
40 DX 1/N
50
FOR I=0 TO N-1 60 F=SQR(1-X^2)
70 X=X+DX
80 A=A+F
90 NEXT I
100 P=4*DX*A
110 PRINT «ЗНАЧЕНИЕ p РАВНО»; P
120 STOP
Слайд 31
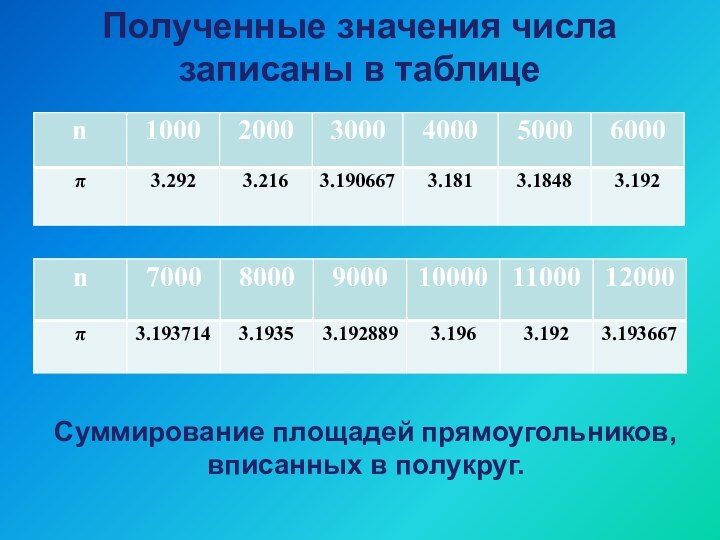
Полученные значения числа записаны в таблице
Суммирование площадей прямоугольников,
вписанных в полукруг.
Слайд 32
Метод Монте-Карло
Это фактически метод статистических испытаний.
Свое экзотическое название он получил от города Монте-Карло в
княжестве Монако, знаменитого своими игорными домами. Дело в том, что метод требует применения случайных чисел, а одним из простейших приборов, генерирующих случайные числа, может служить рулетка. Впрочем, можно получить и при помощи … дождя.
Слайд 33
Метод Монте-Карло
Для опыта приготовим кусок картона, нарисуем на
нём квадрат и впишем в квадрат круг. Если такой
чертёж некоторое время подержать под дождём, то на его поверхности останутся следы капель.
Слайд 34
Метод Монте-Карло
Подсчитаем число следов внутри квадрата и внутри
круга. Очевидно, что их отношение будет приближенно равно отношению
площадей этих фигур, так как попадание капель в различные места чертежа равновероятно. Пусть Nкр - число капель в круге, Nкв – число капель в квадрате, тогда π=4Nкр/Nкв
Слайд 35
Применение метода Монте-Карло стало возможным только благодаря компьютерам
Программа
2
10 REM *** ВЫЧИСЛЕНИЕ ПИ ***
20 REM *** МЕТОД
МОНТЕ-КАРЛО *** 30 INPUT N
40 M=0
50 FOR I=1 TO N
60 T=INT (RND(1)*10000)
70 X=INT(T/100)
80 Y=T-X*100
90 IF X^2+Y^2<10000 THEN M=M+1
100 NEXT I
110 P=4*M/N
120 PRINT " ЗНАЧЕНИЕ ПИ РАВНО" ; P
130 STOP
Слайд 37
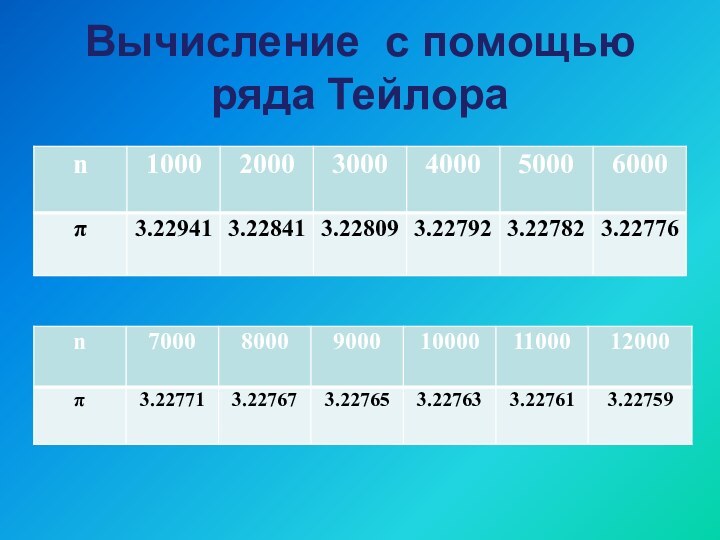
Вычисление с помощью ряда Тейлора
Обратимся к рассмотрению произвольной
функции f(х). Предположим, что для неё в точке x0
существуют производные всех порядков до n-го включительно. Тогда для функции f(х) можно записать ряд Тейлора:
Слайд 38
Вычисление с помощью ряда Тейлора
Программа
REM "Вычисление пи"
REM "Разложение
в ряд Тейлора "
INPUT n
a = 1
FOR i =
1 TO nd = 1 / (i + 2)
f = (-1) ^ i * d
a = a + f
NEXT i
p = 4 * a
PRINT "значение пи равно"; p
END