Слайд 2
Содержание
1 История развития геометрии пирамиды
2 Элементы пирамиды
3 Развёртка пирамиды
4Свойства пирамиды
5Теоремы, связывающие пирамиду
с другими геометрическими телами
6.1 Сфера
6.2 Конус
6.3 Цилиндр
6Формулы, связанные с пирамидой
7Особые случаи пирамиды
8.1 Правильная пирамида
8.2 Прямоугольная пирамида
8.3 Усечённая пирамида
8 Связанные определения
9 Интересные факты
Слайд 3
Что такое пирамида?
Пирами́да (др.-греч. πυραμίς, род. п. πυραμίδος) —
многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие
общую вершину[1]. По числу углов основания различают пирамиды треугольные, четырёхугольные и т. д. Пирамида является частным случаем конуса.
Слайд 5
История развития геометрии пирамиды
Начало геометрии пирамиды было положено
в Древнем Египте и Вавилоне, однако активное развитие получило
в Древней Греции. Первый, кто установил, чему равен объем пирамиды был Демокрит [2], а доказал Евдокс Книдский. Древнегреческий математик Евклид, систематизировал знания о пирамиде в XII томе своих «Начал», а также вывел первое определение пирамиды: телесная фигура, ограниченная плоскостями, которые от одной плоскости сходятся в одной точке.
Слайд 6
Элементы пирамиды
апофема — высота боковой грани правильной пирамиды [3];
боковые грани — треугольники, сходящиеся в вершине пирамиды;
боковые ребра —
общие стороны боковых граней;
вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания;
высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра);
диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания;
основание — многоугольник, которому не принадлежит вершина пирамиды
Слайд 8
Свойства пирамиды
Все диагонали пирамиды принадлежат её граням.
Если
все боковые ребра равны, то:
около основания пирамиды можно описать
окружность, причём вершина пирамиды проецируется в её центр;
боковые ребра образуют с плоскостью основания равные углы.
Если боковые грани наклонены к плоскости основания под одним углом, то:
в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр;
высоты боковых граней равны;
площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани
Слайд 10
Развертка пирамиды
Развёрткой многогранной поверхности называется плоская фигура, получаемая
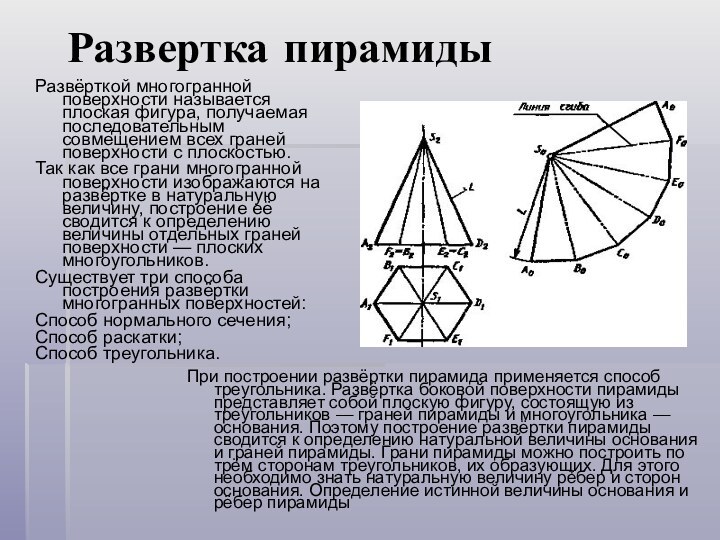
последовательным совмещением всех граней поверхности с плоскостью.
Так как все
грани многогранной поверхности изображаются на развёртке в натуральную величину, построение её сводится к определению величины отдельных граней поверхности — плоских многоугольников.
Существует три способа построения развёртки многогранных поверхностей:
Способ нормального сечения;
Способ раскатки;
Способ треугольника.
При построении развёртки пирамида применяется способ треугольника. Развёртка боковой поверхности пирамиды представляет собой плоскую фигуру, состоящую из треугольников — граней пирамиды и многоугольника — основания. Поэтому построение развёртки пирамиды сводится к определению натуральной величины основания и граней пирамиды. Грани пирамиды можно построить по трём сторонам треугольников, их образующих. Для этого необходимо знать натуральную величину рёбер и сторон основания. Определение истинной величины основания и рёбер пирамиды
Слайд 11
Алгоритм построения
Определяют натуральную величину основания пирамиды (например методом
замены плоскостей проекций);
Определяют истинную величину всех рёбер пирамиды
любым из известных способов (в данном примере натуральная величина всех рёбер пирамиды определена методом вращения вокруг оси перпендикулярной горизонтальной плоскости проекций и проходящей через вершину пирамиды S);
Строят основание пирамиды и по найденным трём сторонам строят какую-либо из боковых граней, пристраивая к ней следующие.
Точки, расположенные внутри контура развёртки, находят во взаимно однозначном соответствии с точками поверхности многогранника. Но каждой точке тех рёбер, по которым многогранник разрезан, на развёртке соответствуют две точки, принадлежащие контуру развёрт
Слайд 12
Теоремы, связывающие пирамиду с другими геометрическими телами
Слайд 13
Сфера
около пирамиды можно описать сферу тогда, когда в
основании пирамиды лежит вписанный многоугольник (необходимое и достаточное условие).
Центром сферы будет точка пересечения плоскостей, проходящих через середины рёбер пирамиды перпендикулярно им. Как следствие из этой теоремы следует, что как около любой треугольной, так и около любой правильной пирамиды можно описать сферу;
в пирамиду можно вписать сферу тогда, когда биссекторные плоскости внутренних двугранных углов пирамиды пересекаются в одной точке (необходимое и достаточное условие). Эта точка будет центром сферы.
Слайд 14
Конус
Конус называется вписанным в пирамиду, если вершины их
совпадают, а его основание вписано в основание пирамиды. Причём
вписать конус в пирамиду можно только тогда, когда апофемы пирамиды равны между собой (необходимое и достаточное условие);
Конус называется описанным около пирамиды, когда их вершины совпадают, а его основание описано около основания пирамиды. Причём описать конус около пирамиды можно только тогда, когда все боковые ребра пирамиды равны между собой (необходимое и достаточное условие);
Высоты у таких конусов и пирамид равны между собой.
Слайд 15
Цилиндр
Цилиндр называется вписанным в пирамиду, если вершина пирамиды
принадлежит его одному основанию, а другое его основание совпадает
с окружностью вписанной в сечение пирамиды плоскостью, параллельной основанию. Причём вписать цилиндр в пирамиду можно только тогда, когда в основании пирамиды — описанный многоугольник (необходимое и достаточное условие);
Цилиндр называется описанным около пирамиды, если вершина пирамиды принадлежит его одному основанию, а другое его основание описано около основания цилиндра. Причём описать цилиндр около пирамиды можно только тогда, когда в основании пирамиды — вписанный многоугольник (необходимое и достаточное условие).
Слайд 16
Формулы, связанные с пирамидой
Объём пирамиды может быть вычислен
по формуле:
где S — площадь основания и h — высота; Боковая
поверхность — это сумма площадей боковых граней:
Полная поверхность — это сумма боковой поверхности и площади основания:
Sp = Sb + So Для нахождения боковой поверхности в правильной пирамиде можно использовать формулы:
где a — апофема боковой грани, P — периметр основания, n — число сторон основания, b — боковое ребро, α — плоский угол при вершине пирамиды
Слайд 17
Особые случаи пирамиды
Правильная пирамида
Пирамида называется правильной, если основанием
её является правильный многоугольник, а вершина проецируется в центр
основания. Тогда она обладает такими свойствами:
боковые ребра правильной пирамиды равны;
в правильной пирамиде все боковые грани — равные равнобедренные треугольники;
в любую правильную пирамиду можно как вписать, так и описать около неё сферу;
если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно , где n — количество сторон многоугольника основания[6];
площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Слайд 18
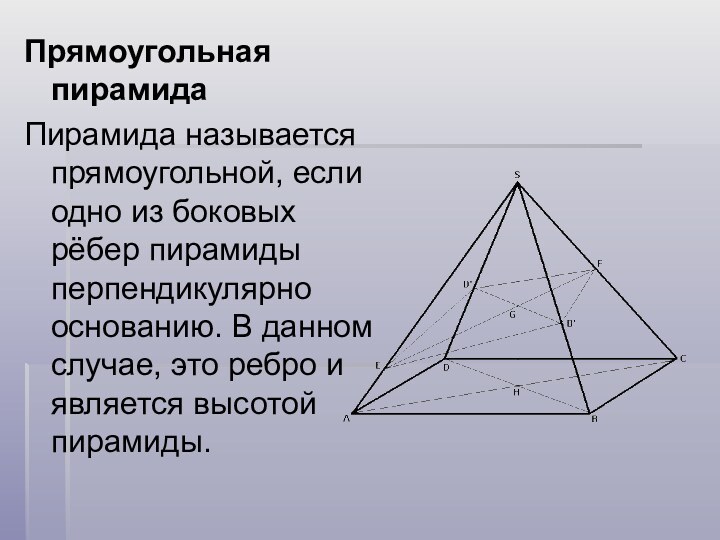
Прямоугольная пирамида
Пирамида называется прямоугольной, если одно из боковых
рёбер пирамиды перпендикулярно основанию. В данном случае, это ребро
и является высотой пирамиды.
Слайд 19
Усечённая пирамида
Усечённой пирамидой называется многогранник, заключённый между пирамидой
и секущей плоскостью, параллельной её основанию.
Слайд 20
Связанные определения
Тетраэдром называется треугольная пирамида. В тетраэдре любая
из граней может быть принята за основание пирамиды. Кроме
того, существуют большое различие в понятиях правильная треугольная пирамида и правильный тетраэдр.





![Фигура пирамида Элементы пирамидыапофема — высота боковой грани правильной пирамиды [3]; боковые грани — треугольники, сходящиеся](/img/tmb/13/1289152/1c4648d01597b0723fd56b5e3f8d7287-720x.jpg)