случаях формулы сокращённого умножения для преобразования целых выражений в
многочлены и для разложения многочленов на множители. из 56
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть


















































из 56
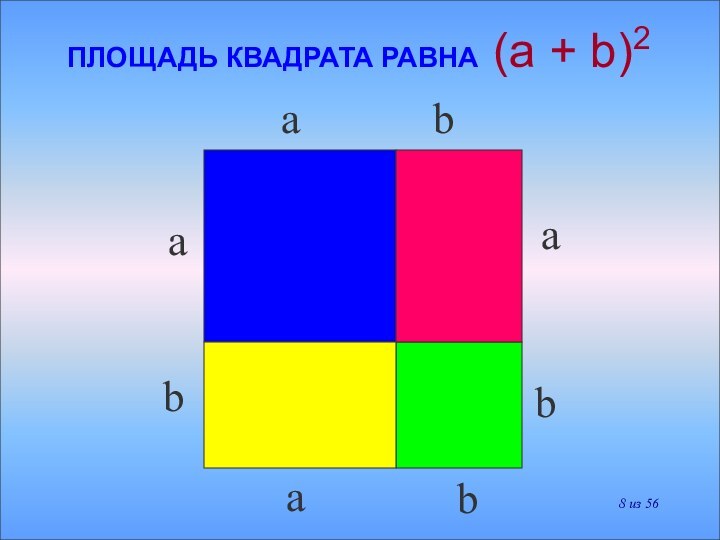
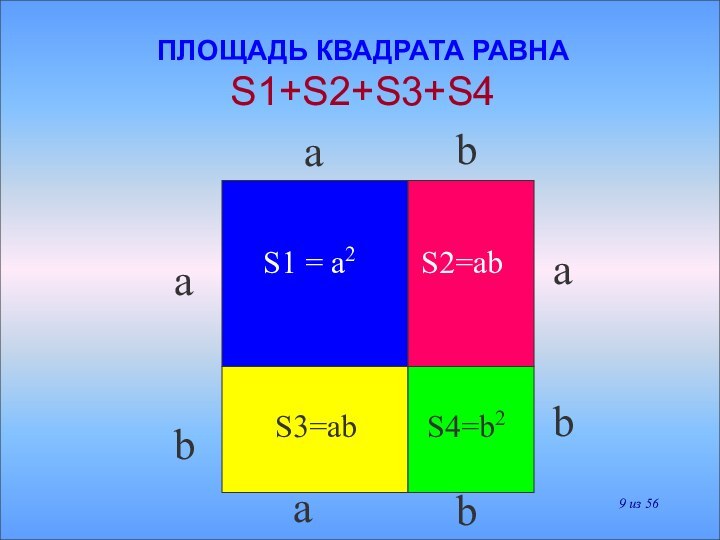
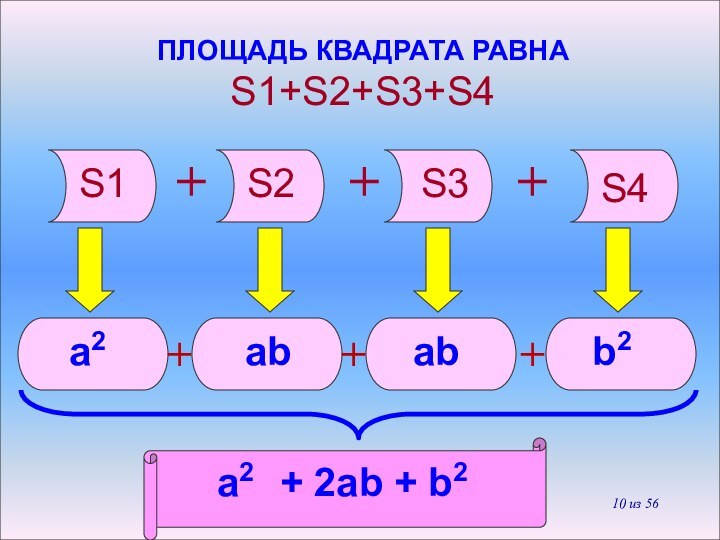
(a+b)2 = a2 +2ab + b2
из 56
из 56
из 56
из 56
2
из 56
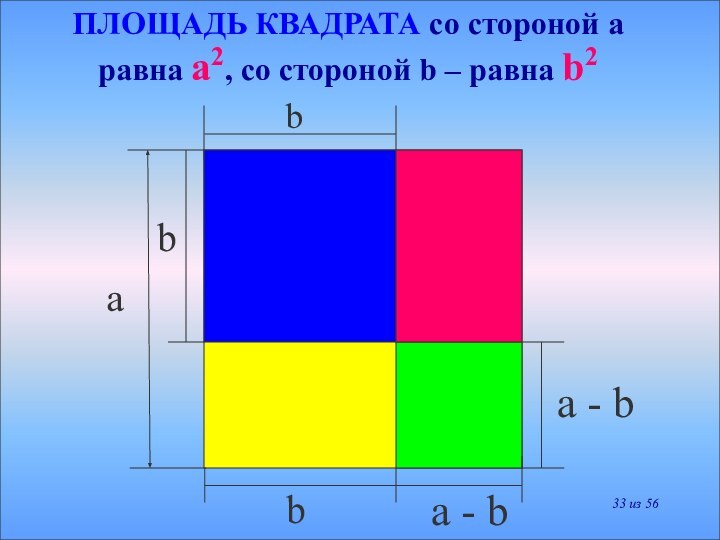
(a - b)2 = a2 - 2ab + b2
из 56
из 56
из 56
из 56
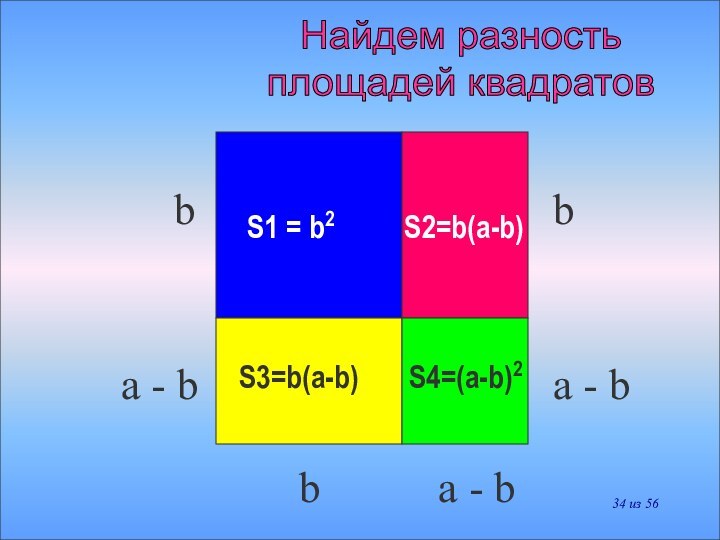
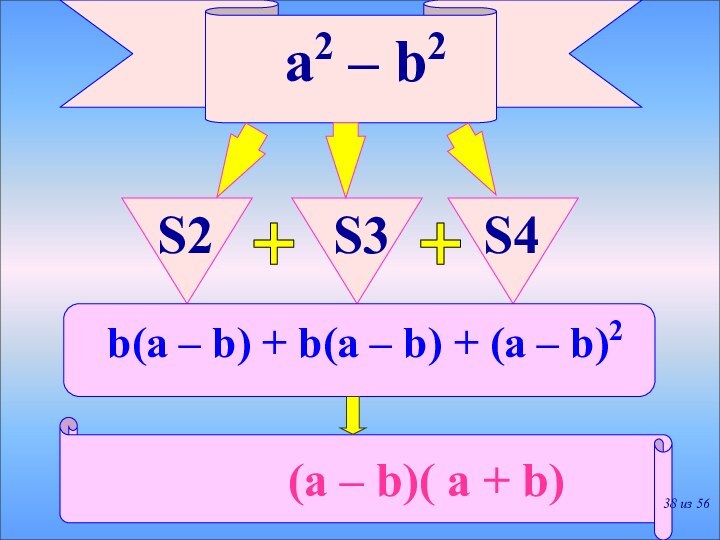
a2 – b2 = (a – b)(a + b)
из 56
из 56
из 56
(a – b)(a + b) = a2 – b2
из 56
из 56
из 56